IAL 30: Cosmology

Don't Panic

Sections

Introduction
Cosmology, Human Concerns, and Philosophy
The Early History of Cosmology (Reading Only)
What of Newtonian Cosmology?
The Expansion of the Universe
Einstein, General Relativity, and the Einstein Universe
The de Sitter Universe
Friedmann Equation (FE) Models
The Accelerating Universe and the Friedmann Equation Λ Models
Dark Energy
The Λ-CDM Model
Cosmological Distance Measures Explained (Reading Only)
The Fate of the Universe According to the Λ-CDM Model
Big Bang Cosmology and the Initial Conditions of the Observable Universe
Limitations and Tensions of our Current Cosmological Theories
Inflation and Inflation Cosmology
Conclusion
Appendix: The Steady State Universe (Not Required for the RHST)
Appendix: The Multiverse Paradigm and Reality (Not Required for the RHST)

Introduction

Physical cosmology---which hereafter we usually just call cosmology---is the science of the universe as a whole and, at just a smaller scale, the large-scale structure of the universe: galaxies, galaxy groups, galaxy clusters, superclusters of galaxies, galaxy filaments, galaxy walls, and voids.

But, of course, it is NOT the science of everything.

The Large-Scale Structure Redux (Reading Only):
We covered the large-scale structure in IAL 29: The Large-Scale Structure of the Universe and can only recapitulate that coverage a bit here in IAL 30: Cosmology.
As an illustration of the large-scale structure large-scale structure, see the figure below (local link / general link: large_scale_structure_z_0x035.html) of the local large-scale structure to cosmological physical distance ∼ 150 Mpc (cosmological redshift z ≅ 0.035) and cosmological physical distance ∼ 300 Mpc (cosmological redshift z ≅ 0.07).
The Ingredients of Cosmology:
To study cosmology entails understanding smaller things than the universe and the large-scale structure of the universe to some degree: e.g., understanding stars, supernovae, super massive black holes, quasars, atoms, molecules, atomic nuclei, electrons, neutrinos, quarks, photons, and dark matter particles (if they exist).
The understanding of the smaller things is only needed insofar as it affects the big things.
In fact, the primary physics essential for cosmology is general relativity.
General relativity is exemplified by curving space, gravitational lensing, and black holes. These effects/objects are illustrated in the two figures below (local link / general link: spacetime_curvature_earth.html; local link / general link: black_hole_gravitational_lensing.html).
Why General Relativity for Cosmology?:
Why general relativity for cosmology?
It is our best theory of gravity and motion under gravity so far.
And it is gravity that determines the motion of the universe as a whole and the evolution of the large-scale structure to 1st order (used in a vague sense).
Newtonian gravity was shown to be inadequate for cosmology as we will discuss below in the section The Early History of Cosmology. So, indeed, the more general theory, general relativity, is needed.
See Isaac Newton (1643--1727) in the figure below (local link / general link: newton_principia.html).
Now most people expect that someday
general relativity will be found to be emergent theory that emerges from a theory of quantum gravity.
Whatever, quantum gravity may be, it will probably have implications for cosmology beyond Λ-CDM model (which we describe below in section The Λ-CDM Model) and which mostly adequately accounts for the observable universe so far. But some revision or replacement in the near future is likely.
In addition to general relativity, cosmology also requires classical physics (including thermodynamics), statistical mechanics, nuclear physics, quantum mechanics, and quantum field theory (which is relativistic quantum mechanics). For the most prominent branches of physics, see the figure below (local link / general link: physics_branches.html).
For the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m), and earlier cosmic times, all the cited branches of physics are needed. Everything comes together in those cosmic times.
After the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m), maybe only general relativity, classical physics (as tool for understanding general relativistic cosmological models) and quantum field theory (for dark energy and dark matter) are needed to explain the observable universe and the a href="http://en.wikipedia.org/wiki/Large-scale_structure_of_the_cosmos">large-scale structure.
Not Cosmology:
There are many things which are definitely excluded from cosmology: e.g., planets, biology, humans, psychology, the Oedipus complex (see the figure below: local link / general link: sigmund_freud.html), etc.
What is the Situation of Cosmology Right Now:
Big Bang cosmology (AKA the Big Bang theory) is the paradigm (i.e., overall grand theory) of cosmology and has been so since the 1960s. It is so well established that it would be astonishing if it were just plain WRONG.
Big Bang cosmology is well established because it explains a lot about the observable universe and there is strong evidence for it (see subsection Summary of the Strongest Evidence for Big Bang Cosmology below) for which NO other theory explains adequately at all. And it's NOT for lack of trying to find alternative theories.
So Big Bang cosmology is NOT speculative science anymore: it is probably essentially right as far as it goes.
The particular quantitative version of Big Bang cosmology that now holds sway is the Λ-CDM model which mostly adequately accounts quantitatively for the observable universe so far.
But, as aforesaid in subsection The Ingredients of Cosmology, the Λ-CDM model might turn out to need significant revision or even replacement, but time will tell on that.
However, NEITHER Big Bang cosmology NOR the Λ-CDM model in themselves tell us everything we would like to know.
We take up this subject in detail in section Limitations and Tensions of our Current Cosmological Theories.
Beyond Big Bang Cosmology:
Issues outside of Big Bang cosmology are dealt with in broader theories which could better be called paradigms (i.e., overall grand theories). Those paradigms are more speculative and may well be just WRONG.
Currently, only two beyond-the-Big-Bang paradigms have much of a vogue: inflation (very much the frontrunner) and the cyclic universe in various versions (e.g., the ekpyrotic universe) (very much the hindmost).
We will discuss inflation and, briefly, the cyclic universe below in the section Inflation and Inflation Cosmology.
But we will give a brief introduction to inflation here.
Inflation is actually paradigm with many precisely specified versions: i.e., theories of inflation.
Basic inflation sets the initial conditions for the Big Bang in a rather satisfying manner.
But we do NOT know which of the precisely specified theories of inflation is correct if any NOR even which one is most adequate.
In the opinion of many (including yours truly), inflation is a useful paradigm for furthering research, but NOT yet so well established that it would be astonishing if it were just plain WRONG.
Beyond basic inflation are more elaborated, speculative versions of inflation (NOT essential to the inflation paradigm) which try to explain the whole universe, observable and unobservable.
A prominent one of the speculative versions is called eternal inflation.
A fair number of astronomers (including yours truly) think a qualitative version of eternal inflation is a plausible theory of the whole universe without putting any great faith in it. It just gives us something to put in the slot "theory of the whole universe".
We discuss eternal inflation below in subsections Eternal Inflation and Eternal Inflation Further Explicated.
By the by, eternal inflation as well as being an inflation theory is also a multiverse paradigm theory. See section Appendix: The Multiverse Paradigm and Reality (Not Required for the RHST) for some incoherent rambling on the multiverse paradigm theory and reality.

Cosmology, Human Concerns, and Philosophy

Cosmology in the broad sense has always been of importance to humankind.

We are concerned about the meaning, purpose, and nature of our own existence.

Therefore about the meaning, purpose, and nature of the universe which sustains us and everything else.

See angel of melancholia reflecting on the meaning, purpose, and nature of the universe in the figure below (local link / general link: melancholia.html).

Meaning, Purpose, Nature:
Modern physical cosmology of course, concerns itself with NATURE OF and leaves aside MEANING AND PURPOSE.
But MEANING AND PURPOSE probably hover somewhere just beyond the expressed concerns of many modern scientific cosmologists and are probably of interest to everyone interested in cosmology.
If we ever did finally fathom the universe, it is easy to believe that that knowledge would have PHILOSOPHICAL IMPLICATIONS.
But modern scientific cosmologists are usually---but NOT always---reluctant to connect current thinking with philosophical theories.
They are well aware that modern cosmological theories may well be WRONG or SUPERFICIAL, and so drawing philosophical conclusions is premature---and, of course, we are NOT sure know how to draw them accurately anyway. But one can ponder: see the figure below (local link / general link: the_thinker.html).
Of course, it is possible to draw correct conclusions from a wrong theory, but that's NOT very likely.
One can go the other way and try to derive or constrain cosmology from philosophical ideas.
Using philosophical ideas as a source of interesting cosmological hypotheses in research via scientific method is valid as long as the hypotheses are NOT taken as dogma, but as things to be tested empirically.
The Reluctant Cosmologist:
For an example of a reluctant cosmologist, consider cosmologist Georges Lemaitre (1894--1966) who was a Roman Catholic priest.
Lemaitre resisted identification of his primeval atom theory with the creation of Genesis. The former was speculative science; the latter, faith.
The primeval atom is the theoretical ancestor of Big Bang cosmology (see No-525,530; Jean-Pierre Luminet, The Rise of Big Bang Models (4) : Lemaitre, 2015).
Images of Lemaitre are given in the figure below (local link / general link: georges_lemaitre.html).
The Bad Old Days:
In the past, cosmologists have NOT been so circumspect about the PHILOSOPHICAL IMPLICATIONS of physical cosmology.
Myth-oriented cosmologists and philosophical cosmologists were or are often concerned with these implications.
See a couple of the old bulls in the figure below (local link / general link: aristotle_plato.html).
Certainly, it's useful to consider
philosophy in science provided you don't take your own idiosyncratic ideas too seriously.
Who's to say when the next great advance in understanding in philosophy will come and clarify things for us.
As the figure below (local link / general link: pan.html) suggests perhaps one is forced to admit "Those cosmologists, they don't know nothing."

The Early History of Cosmology (Reading Only)

Here we tackle the early history of cosmology, and so necessarily recapitulate some of the story of IAL 4: The History of Astronomy to Newton.

Mythical Cosmologies:
See the discussion in the figure below (local link / general link: leonardo_da_vinci_deluge_creation.html).
Hesiod (fl. 700 BCE) is illustrated in the figure below (local link / general link: hesiod.html).
The upshot of the second to last figure (
local link / general link: leonardo_da_vinci_deluge_creation.html) is that it seems humankind are predisposed to think that there must be a relatively simple beginning in time---or more abstractly outside of time---as Boethius (c.477--524) thought. For Boethius, see the figure below (local link / general link: boethius.html).
But is this true? Certainly, modern physical cosmology thinks so---in time and/or outside of time.
The Pre-Socratic Philosophers Redux:
The ancient Greek Pre-Socratic philosophers beginning in the 6th century BCE are the first persons recorded in history to try to develop philosophical theories about the universe---by philosophical theories, your truly means those subject to argument, empirical investigation, and correction.
The Pre-Socratics were---compared to modern standards---weak on detailed observation and experimentation---they did practise them at least a little at times---and this weakness limited their progress in cosmology and all other sciences as well. They relied on casual observations and reasoning and argument. Their understanding of what we call the scientific method was poor.
One can characterize much of the theorizing of the Pre-Socratic philosophers as the making of RATIONAL MYTHS.
Some of their theories are very interesting.
The cosmology of the Greek atomist philosophers Leucippus (first half of 5th century BCE) and Democritus (c.460--c.370 BCE) posited infinitely many worlds forming in vortices out of an infinite space of atoms in motion (see Wikipedia: Democritus: Anthropology, biology, and cosmology). See the two figures below (local link / general link: democritus.html; local link / general link: cosmology_atomist.html) and the subsection Early Cosmology Videos at the end of this section.
The
atomist cosmology with its vortices was certainly suggested by the daily rotation of the celestial sphere.
The figure below (local link / general link: gemini_north_swirl.html) showing a long-exposure image makes Democritus' thinking plausible.
Democritus (c.460--c.370 BCE) didn't have long exposure images, but he could watch the sky swirl around any clear night---an in pre-industrial times, people were much more conscious of the behavior of the sky and could see it better without light pollution.
Aristotelian Cosmology:
In western Eurasia, the cosmological theory that became dominant in Classical Antiquity and then in the Islamic Golden Age (c.8th--c.14th centuries) (see figure below) ...
... and Medieval Europe (see the figure below: local link / general link: joan_of_arc.html) ...
... was that of
Aristotle (384--322 BCE) (see the figure below: local link / general link: aristotle_supreme.html)--who was a post-Socratic philosopher.
In
Aristotelian cosmology, the Earth was at the center of an eternal, bounded, finite, spherical universe.
The boundary was a real physical celestial sphere of the stars on which the stars were pasted: the planets were closer and held on compounded other celestial spheres which were moved by gods or in monotheistic contexts by angels.
See a cartoon of Aristotelian cosmology in the figure below (local link / general link: aristotle_cosmos.html).
Dante Alighieri (1265--1321) assumed Aristotelian cosmology in his Divine Comedy as illustrated with some artistic license in the figure below (local link / general link: dante_beatrice.html).
Beyond the
celestial sphere of the stars was nothing: NOT even empty space---even in Classical Antiquity a lot of people found this "NOT even empty space" part hard to accept. What if you stood at the boundary of the celestial sphere of the stars and thrust a spear outward? See the figure below (local link / general link: aristotle_hoplite_spear.html). What would happen? Aristotle gives no answer.
Aristotelian cosmology actually bears a passing resemblance to the Einstein universe which we discuss below in the section Einstein, General Relativity, and the Einstein Universe.
The Copernican Revolution:
The small Aristotelian universe was put in doubt to the astronomically-minded by Nicolaus Copernicus's (1473--1543) Copernican heliocentric solar system of 1543.
First of all, by putting the Sun in the center of the Solar System, of course.
Heliocentrism also upset the Aristotelian universe by requiring the fixed stars to be extremely remote: this is the only reasonable way that the Earth could move and the fixed stars NOT show stellar parallax in pre-modern observations.
An Infinite Universe?
But if the stars were very remote why should they be pasted on a big sphere (the celestial sphere of the stars)?
Why NOT an infinity of stars spread throughout an infinite universe? or at least a quasi-infinity of stars spread throughout a quasi-infinite universe? Quasi meaning "seemingly" in this context.
In the context of Copernican heliocentrism, the idea of an infinity of stars spread throughout an infinite universe was first put forward by Thomas Digges (1546--1595) in 1576 (No-296). See the figure below (local link / general link: copernican_cosmos_digges.html).
As heliocentrism gained credence and the telescope revealed a quasi-infinity of new stars and that the Milky Way was a band of stars, the notion of an infinite or very large universe filled with stars became plausible.
The Sun could NOT be considered the center of this kind of universe. Sooner of later, it became clear the Sun was just another star---but it is our star.
The History of Cosmology in the IALs: The history of astronomy up to the time of Isaac Newton (1643--1727) is the history of cosmology since the astronomy and cosmology were almost synonyms. So we, in fact, described the history of cosmology to Isaac Newton (1643--1727) in IAL 4: The History of Astronomy to Newton and reviewed it above in this section. What of the time of Newton and after? Well, Newtonian physics ended the synonymousness the history of astronomy and the history of cosmology since it showed how the celestial mechanics of the Solar System and by extension other planetary systems (which could be assumed exist) followed from physical law. But it was NOT clear how Newtonian physics applied to the whole universe which was now known to be vast. So a lot of astronomy could be done not saying anything about the whole universe and a lot of astronomy followed that path of not saying anything. In IAL 26: The Discovery of Galaxies, we reviewed history of the cosmology that led to modern cosmology from Ptolemy (c.100--c.170 CE) to Edwin Hubble (1889--1953) in 1924 largely in from observational point of view in subsections:
1. The History of the Discovery of the Milky Way.
2. The Discovery of Galaxies: An Example of the Process of the Scientific Method.
From the theoretical history of cosmology is described in the aforementioned IAL 4: The History of Astronomy to Newton. The history of modern cosmology starting from the work of Edwin Hubble (1889--1953) and Albert Einstein (1879--1955) is effectively described below in the rest of IAL 30: Cosmology along with contemporary cosmology. Below in section What of Newtonian Cosmology?, we do describe useful subject of Newtonian cosmology from Newton to the present day.
Early Cosmology Videos:
See the Early cosmology videos below:

Group Activity:

Form groups of 2 or 3---NOT more---and tackle Homework 4 problems 8--13 on ancient Greek astronomy.

Discuss each problem and come to a group answer.

Let's work for 5 or so minutes.

The winners get chocolates.

See Solutions 4.

What of Newtonian Cosmology?

What can one do in cosmology with Newtonian physics: i.e., what of Newtonian cosmology?

We present a certain amount of the answer in the insert below (local link / general link: newtonian_cosmology.html).

The Expansion of the Universe

When did the theory of the expansion of the universe enter history?

The Static Universe Theory:
After the Copernican revolution of the 16th and 17th centuries, the vague ideas of the universe as quasi-infinite with a quasi-infinity of stars gained ground and Newton believed them as we mentioned above in subsection Isaac Newton (1643--1727) and the Universe.
From 17th century to the early 20th century, the vague ideas astronomers had on the universe evolved a bit. It seems that they thought either there was a finity of stars in the Milky Way with nothing beyond OR there was a quasi-infinity of stars organized into galaxies which extended to quasi-infinity.
Without polls from the past, it's hard to know what were the actual opinions of astronomers back then.
The definitive proof of the existence of other galaxies in 1924 (see Wikipedia: Edwin Hubble: Universe goes beyond the Milky Way galaxy; No-510) clarified one issue.
Another basic idea of cosmology that persisted up to circa the 1920s was that the universe was essentially STATIC: the stars and other galaxies (assuming they existed) were NOT moving on average even though stellar peculiar velocities were known.
Without having a poll from the past, it is hard to know how many astronomers thought the universe was essentially STATIC, but certainly it was held by Einstein in circa 1915--1929 who evidently thought it was accepted theory initially. See Einstein hanging out with the guys in the figure below (local link / general link: einstein_olympian.html).
The belief in a STATIC
universe is actually odd since the universe was obviously NOT thermodynamically static: i.e., it is NOT in thermodynamic equilibrium.
Heat energy is steadily being lost to stars as energy flows out of them in the form of electromagnetic radiation (EMR) and NOT being returned.
Even before the development of thermodynamics in the 19th century, people were aware in sense of the problem of the universe NOT being in thermodynamic equilibrium in a sense via Olbers's paradox: see figure below (local link / general link: olbers_paradox.html).
The
universe being NOT thermodynamically static was evident after the development of thermodynamics in the 19th century.
Why should the universe, which was so obviously evolving thermodynamically, be automatically assumed to be dynamically static on average? If evolving in one way, it could well be evolving in other ways?
To us, it seems natural to think it could be evolving in other ways, but somehow this idea was resisted before circa 1920.
Evidence for Large-Scale Motions in the Universe:
Actually there was evidence before 1920s for large-scale motions of the observable universe.
See the figure below (local link / general link: vesto_slipher.html) on the work of Vesto Slipher (1875--1969).
Redshifts:
The cosmological redshift is explicated (along with some discussion of the Doppler effect) in the figure below (local link / general link: cosmological_redshift.html).
Back to Redshifted Galaxies:
But what was the FLOW PATTERN of the receding galaxies?
To know this you had to know, in addition to recession velocities, distances to the galaxies: i.e., where the galaxies were in space.
Hubble and the Expansion of the Universe:
By 1929, Hubble had distances to 46 galaxies beyond the Milky Way including 4 in the Virgo Cluster (a nearby large galaxy cluster) (Wikipedia: Edwin Hubble: Redshift increases with distance; Hubble 1929; No-510, but some errors). But only 24 of these distances were for independent and could be used in his analysis???.
Note that Hubble could only get Cepheid distances to the Andromeda Galaxy (M31) and the Triangulum Galaxy (AKA M33) ??? (No-510). That is about as far as he could observe Cepheids. For greater galaxy distances, he had to use less-reliable distance indicators from his early version of the cosmic distance ladder. Those less-reliable distance indicators had large systematic errors and random errors. So his distances were NOT too good---but they were good enough for his most famous discovery.
Using
Slipher's redshifts and maybe other redshifts, Hubble was able to find a remarkably simple relationship between distance and recession velocity (No-523).
The observational relationship found by Hubble, first presented in 1929, is now called Hubble's law.
Hubble extracted Hubble's law from a Hubble diagram.
For Hubble's law and a modern Hubble diagram for the very nearby local universe, see the figure below (local link / general link: hubble_diagram.html). A more detailed caption appears in the next subsection (i.e., subsection Further Explication of the Hubble Diagram).
The
Hubble constant is often called the rate of expansion of the universe.
Actually, it is the relative rate of expansion of the universe (i.e., the rate of expansion of the universe per unit cosmological physical distance) This is clear from the formula above with the interpretation of r as cosmological physical distance: i.e., the distance measured at one instant in cosmic time (which we discussed in IAL 26: The Discovery of Galaxies and which we will discuss further below).
Hubble's original favored value for H_0 (which he called K) was 500 (km/s)/Mpc (Hubble 1929, 3rd to last paragraph; Bo-39; Tamann 2005; Wikipedia: Timeline of Hubble constant values).
Hubble had large systematic errors in his distance values, and so his value for H_0 was rather badly wrong.
Circa 2021, the value of the Hubble constant has NOT been absolutely agreed. Two possibilities that do NOT agree within error are ∼ 68 (km/s)/Mpc and ∼ 73 (km/s)/Mpc (see Wikipedia: Timeline of Hubble constant values) .
For this lecture, we will usually write
```
  H=70*h_70 (km/s)/Mpc, 

  where h_70=H/(70 (km/s)/Mpc) is a fiducial reduced Hubble constant.
```
This is a standard way of writing the Hubble constant leaving the actual value general, but indicating a fiducial value, in this case 70 (km/s)/Mpc. The fiducial value must be correct to within a few percent.
Hubble's law shows that there is a general expansion of the universe and that the relative rate of expansion. Hubble constant.
So Hubble had observationally discovered the expansion of the universe and that it obeyed Hubble's law.
However, there was some debate how about how much credit Hubble should get and how much others should get. We take up this fine point in the history of astronomy in subsection Who Discovered the Expansion of the Universe and Hubble's Law? in section Friedmann Equation (FE) Models below.
Further Explication of the Hubble Diagram (Reading Only):
Hubble extracted Hubble's law from what we now call a Hubble diagram as aforesaid in subsection Hubble and the Expansion of the Universe.
See the example Hubble diagrams in the figure below (local link / general link: hubble_diagram.html).
In the
Hubble diagram just above, the line is the representation of Hubble's law and the slope of the line is the Hubble constant.
Hubble's law shows that there is a general growth of distances between extragalactic objects when the redshift of remote objects is correctly interpreted as the cosmological redshift.
As mentioned above, this general growth is called the expansion of the universe.
Based on direct and indirect observations, everything up to the present indicates the recession velocity (NOT recession velocity plus peculiar velocity) is exactly linear with cosmological physical distance.
The exact linearity of the theoretical Hubble's law is predicted by all the common cosmological models based on general relativity.
So observations and theory agree on Hubble's law---a triumph for both of them.
But we CANNOT verify Hubble's law for large physical distances by direct observations.
This is because the at-one-instant-in-cosmic-time recession velocities and physical distances are NOT direct observables beyond about the z ≤ 0.5 local universe. They are dependent on the cosmological model adopted, and so have that model's uncertainty.
We CANNOT observe galaxies and other remote objects (e.g., quasars, supernovae, and gamma ray bursts) at the current cosmic time, but only as they were in the past.
Is there a center of the universal expansion?
There is ASSUMPTION in cosmology called the Copernican principle: it states that we occupy NO special place in the observable universe. This principle is a guiding simplifying principle in cosmology.
We have no observational evidence or broadly accepted theoretical reason for thinking it is false. In fact, as far as we can tell it seems true.
Understanding the Expanding Universe:
The figure below (local link / general link: expanding_universe.html) shows how to understand the expanding universe.
Is There a Center of Expansion and Something to Expand Into?:
Is there a center of expansion and something to expand into?
In Friedmann equation (FE) models (see section Friedmann Equation (FE) Models), there is NOT.
The expansion is everywhere and started from a state of infinite density or very high density which was everywhere. Everywhere has grown. The universe has just been growing and is NOT expanding into anything.
On the other hand, maybe there is a center somewhere and something to expand into in some sense, and the FE models describe only a portion of the whole universe. Such a whole universe would NOT homogeneous and isotropic as the observable universe is approximately at least approximately.
So we do NOT know the answer to the question "Is there a center of expansion and something to expand into?"
Summary of this Section:
To summarize this section, we have the observed expansion of the universe. Since the universe seems homogeneous and isotropic, there is no apparent center of expansion and NO reason to believe the universe is expanding from some region or expanding into any region.
As far as we can tell observationally, expansion of the universe is a general scaling up of distances between gravitationally unbound systems.
We also know that general relativity (GR) is our best theory of gravity and spacetime.
So how do we explain the universe and the expansion of the universe?
We'll see in the sections below.

Group Activity:

Form groups of 2 or 3---NOT more---and tackle Homework 30 problems 2--5 on cosmology and Hubble's law.

Discuss each problem and come to a group answer.

Let's work for 5 or so minutes.

The winners get chocolates.

See Solutions 30.

Einstein, General Relativity, and the Einstein Universe

In discussing the expansion of the universe and Hubble's law in section The Expansion of the Universe, we have historically got to 1929 and some later developments in observations plus a little theoretical cosmology.

However, we have to now return to 1917 to pick up the full story in theoretical cosmology.

Introduction to Einstein Et Cetera:
Albert Einstein (1879--1955) in 1905 presented his theory of special relativity which among other things gave the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns as the highest physical speed (i.e., highest speed of motion relative to a local inertial frame) and showed that the flow of time was frame-dependent (which effect is called time dilation).
But special relativity does NOT deal satisfactorily with gravity from all relevant perspectives.
Hence, Einstein went on to develop general relativity with the complete theory presented in 1915.
In this section, we see how Einstein applied general relativity in cosmology.
For a review of general relativity, see IAL 25: General Relativity, subsections:
Prologue to the Einstein Universe (1917):
Albert Einstein (1879--1955) (see figure adjacent and below: local link / general link: einstein_master_1921.html) posited general relativity (1915) as a universal physical law which means it should apply everywhere in the universe.
But that means general relativity should apply to the largest scale structure of universe assuming that gravity determines the largest scale structure of the bulk universe---which we believe to be true.
In other words, if general relativity was truly a universal physical law, it must be able to give a self-consistent cosmological model: i.e., a model of the whole universe.
Showing that it did so was a necessary verification of general relativity and Einstein did, in fact, pursue that verification.
Note Einstein's immediate concern was that such self-consistent cosmological model was possible, NOT that it was the actual true self-consistent cosmological model of the universe. But Einstein did eventually come to hope that his cosmological model (which we call the Einstein universe (1917)) would be the right one. To let the cat out of the bag, the Einstein universe is a STATIC cosmological model: it does NOT expand or contract.
We know Einstein came to hope the Einstein universe was true because it took him until 1931 abandon it. He only did so after accepting the expansion of the universe (two years after Edwin Hubble (1889--1953) had shown it definitively in 1929) and some years after the Einstein universe had been shown to be unstable: i.e., it would necessarily evolve into a cosmological model in simplest approximation in general expansion or contraction or, in more realistic approximation, into a cosmological model with expanding and contracting regions (see Cormac O'Raifeartaigh et al., Einstein's 1917 Static Model of the Universe: A Centennial Review, 2017, p. 40--41).
For much more detail about the history of the Einstein universe than we give below, see Cormac O'Raifeartaigh et al., Einstein's 1917 Static Model of the Universe: A Centennial Review, 2017 and Cormac O'Raifeartaigh, Historical and Philosophical Aspects of the Einstein World, 2019. More detial is in Bo-97 and No-520.
The Einstein Universe: A Physically Consistent Cosmological Model and an Exact Solution:
The Einstein universe (1917) is, in fact, probably the first cosmological model developed from an exact mathematical physics theory and completely consistent with that exact mathematical physics theory---counting the cosmological constant (see below) as part of that exact mathematical physics theory (i.e., general relativity).
The Einstein universe is also, in fact, the only exact (analytic) solution in general relativity that Einstein ever obtained himself as far as yours truly knows. And it is only a special case of one of the only 6 top-level (i.e., general and important) exact solutions in general relativity. For further explication of exact solutions in general relativity, see the figure below (local link / general link: general_relativity_exact_solutions.html).
Einstein's Simplifying Assumptions for the Einstein Universe:
In order to apply general relativity (GR) to the universe, Einstein made 3, major simplifying ASSUMPTIONS, the first 2 of which are still usually used today for the observable universe above the scale of the large-scale structure of the universe.
We explicate the 3, major simplifying ASSUMPTIONS in the subsubsections below.
1. The Cosmological Principle Assumption:
  The cosmological principle is a glorified expression for the assumption that the universe looked at averaged over sufficiently large scales is homogeneous (i.e., the same everywhere at one time) and isotropic (i.e, the same in all directions).
  The cosmological principle is explicated in the figure (local link / general link: observable_universe_cosmological_principle.html).
  Einstein in 1917, of course. did NOT have our modern observations and did NOT know if other galaxies existed beyond Milky Way. Many astronomers still thought they did NOT exist and Einstein followed their lead, maybe without much thinking.
  So for Einstein, the universe was one full of stars, NOT galaxies and the cosmological principle for him meant that the stars were homogenously and isotropically spread throughout space on average.
  By the by, Einstein's knowledge of astronomy was NOT extensive in 1917 though in later years he became much more knowledgeable. He came to astronomy from a pure physics background.
  The term cosmological principle was NOT used by Einstein, at least NOT in 1917. It was coined in 1935 by E.A. Milne (1896--1950): see the figure below local link / general link: e_a_milne.html.
2. The Perfect Fluid Assumption:
  This assumption is that the mass-energy of the universe can be approximated as a homogeneous, isotropic, perfect fluid which in the older literature was sometimes called the substratum (Bo-65,75--76).
  A perfect fluid has NO heat conduction, NO viscosity, and NO shear stress. It can have pressure. In cosmological models baryonic matter is assumed to have zero pressure---which is a good approximation for cosmological models above the scale of the large-scale structure (see Li-39). The cosmic background radiation (CBR) has significant pressure only at very early cosmic time in Big Bang cosmology: i.e., in the radiation era (inflation end 10**(-32) s ? -- 51.7(8) kyr). The simplest form of dark energy (beyond calling the cosmological constant (AKA Lambda, Λ)) formally has constant NEGATIVE PRESSURE, but since the dark energy stuff (whatever that is) does NOT pull on anything, except itself, this NEGATIVE PRESSURE has NO effect. We discuss dark energy below in subsection The Introduction of the Cosmological Constant.
  Einstein assumed zero pressure which, in fact, all cosmological models did (after the end of the radiation era (inflation end 10**(-32) s ? -- 51.7(8) kyr)) before circa 1998.
  By using the perfect fluid assumption the Einstein universe and, in fact, most cosmological models for the observable universe as whole do NOT deal directly with stars, galaxies, and the large-scale structure of the universe. So now for a question on assumptions in theorizing.
  For Occam's razor, see figure below (local link / general link: william_of_ockham.html).
3. The Static Universe Assumption:
  Einstein assumed the universe was STATIC which in fact is a WRONG assumption since there is an expansion of the universe, but this was NOT known until the 1920s either observationally or theoretically. There may have been a few astronomers thinking of it for hypothetical other galaxies, but Einstein (who had a non-astronomy background) was probably NOT aware of that thinking.
  Recall that for Einstein in 1917 the universe was one full of stars, NOT galaxies and the cosmological principle for him meant that the stars were homogenously and isotropically spread throughout space on average (see the subsubsection The Cosmological Principle Assumption above).
  So by a STATIC universe, Einstein was thinking of a STATIC (on average) distribution of stars.
  Why did he make this assumption?
  Possible and certain reasons:
  1. As aforementioned, the observational and theoretical discoveries of the expansion of the universe were in the 1920s, and so there was NO absolute objection to a STATIC universe in 1917.
    This is a certain reason.
  2. It seems that many astronomers were still thinking in 1917 of a STATIC distribution of stars as being the structure of the universe (Bo-75).
    Perhaps, they were still thinking of the stars as being at rest in Isaac Newton's (1643--1727) absolute space.
    It's hard to know what was majority opinion in 1917 since there are NO opinion polls from 1917 on cosmology.
    So it may be that Einstein was simply following what he believed to be the general belief that the universe was STATIC.
    This is a possible reason.
    Why a good physicist like Einstein---to say the least---should defer to a bunch of astronomers is beyond me especially since the obvious non-thermodynamic equilibrium state of the universe (which we discussed above in the subsection The Static Universe Theory pointed to an evolving universe.
  3. Einstein may have thought that the STATIC universe was the simplest hypothesis and therefore the choice of Occam's razor.
    If so, this was WRONGwrong as we now know. But we know this because we have the Friedmann equation which is derived from general relativity. Somehow Einstein missed deriving the Friedmann equation and derived the Einstein universe directly from general relativity in a klutzy way. His derivation was a pioneering effort.
  4. Einstein in 1917 had a strong belief in Mach's principle which we will NOT describe (see Wikipedia: Mach's principle; Bo-97--98; Fre-543). His belief in Mach's principle made him believe that it had to be incorporated in a cosmological model for the cosmological model to be correct and he seems to have believed Mach's principle required a STATIC universe (see Cormac O'Raifeartaigh, Historical and Philosophical Aspects of the Einstein World, 2019, p. 10,14,19).
    In later years, Einstein (or so yours truly recalls from some long ago reading) dismissed Mach's principle as perhaps WRONG since it is NOT inherent in general relativity and was NOT required by cosmology as it had developed.???? The situation is the same today: Mach's principle may have some truth to it, but nothing demands it. In fact, there seems little interest in Mach's principle anymore.
The Introduction of the Cosmological Constant:
In fact, Einstein found that he could NOT find a STATIC MODEL or ANY MODEL with GR as he had originally proposed it (No-520).
There were such cosmological models to be found as we discuss below in section Friedmann Equation (FE) Models, but in his pioneering work, Einstein could NOT find them. Remember he was starting out without all the mathematical tricks for general relativity that he and others would find in the decades after 1917.
Einstein's path to finding any cosmological model led him to introduced the cosmological constant which we explicate along with dark energy in the insert below (local link / general link: lambda_cosmological_constant_dark_energy.html).
The Einstein Universe:
Einstein's STATIC MODEL is now called the Einstein universe. Geometrically, it is the 3-dimensional surface of a sphere in a 4-dimensional Euclidean space. Such a "sphere" is called a hypersphere. Thus, the Einstein universe is a finite, but unbounded, hyperspherical space (No-520; Bo-98).
Note, the 4-dimensional Euclidean space is given NO physical interpretation since general relativity does NOT imply it exists in any sense. There is just the curved "surface space".
Now we have difficulty picturing curved 3-dimensional spaces, but the 2-dimensional analogs of curved spaces can pictured. See the figure below (local link / general link: universe_geometry.html).
Actually, I wonder how well we picture 3-dimensional flat space. Maybe we only picture it in the sense that experience and intrinsic mental and sense abilities inform us how things look in other directions from the one we are viewing an object from.
The Einstein universe is analogous to the surface of an ordinary sphere in the figure below (local link / general link: universe_geometry.html).
In such a space traveling in a straight line (a line that seems to be straight at every locality) should bring you back to where you started and if you looked long enough in one direction you should see the back of your head.
A "straight line" in curved space is geodesic---the stationary path (the shortest path in most considered examples) between any two points in the curved space.
For a recapitulation of the description of the
Einstein universe (1917) with some different points made, see see the figure below (local link / general link: universe_einstein.html).
The Einstein Universe is Unstable:
The Einstein universe is actually in unstable equilibrium (Bo-118; No-527). Any perturbation will start it on a runaway expansion or contraction.
The cartoon in the figure below (local link / general link: stability_mechanical.html) illustrates stable and unstable equilibriums.
Exactly how the many local perturbations that exist in any real universe could have affected a real Einstein universe is hard to say. However, one idea of how a perturbed Einstein universe would behave is discussed below in subsection Avoiding the Singularity.
Einstein Abandons the Einstein Universe:
After 1929 and the observational discovery of expansion of the universe (No-523) and discussions with many researchers including Edwin Hubble (1889--1953) in 1930 (No-526), Einstein abandoned the Einstein universe and subsequently very probably said introducing the cosmological constant to obtain the Einstein universe was his "biggest blunder" (though only in private and perhaps NOT in those exact words: he may have been speaking in German) to George Gamow (1904-1968) and maybe others (see O'Raifeartaigh & Mitton 2019, p. 22--23).
Actually, Einstein's abandonment of the Einstein universe was a long and complex process in which its instability seems to have been the primary reason for abandonment (see Nussbaumer 2013).
Recall Einstein originally in 1917 was NOT trying to establish the true cosmological model, but merely that general relativity allowed a self-consistent cosmological model to exist. But it seems he became hopeful after circa 1917 that the Einstein universe was the true cosmological model.???
Whatever Happened to the Cosmological Constant?
The cosmological constant was a mistake in its original use, but it didn't go away.
It continued to be useful for other cosmological fix-ups---"the last refuge of scoundrel cosmologists" (Michael Turner 2011)---and, in fact, it has come back in a new function with a vengeance as we'll see below the section The Accelerating Universe and the Friedmann Equation Λ Models.
But though Einstein blundered, others did NOT: expansion of the universe was predicted from GR models before it was observationally discovered as we'll see below in the section Friedmann Equation (FE) Models.
To Finish: Einstein Videos:
See Einstein videos below (local link / general link: einstein_videos.html).

Group Activity:

Form groups of 2 or 3---NOT more---and tackle Homework 30 problems 2--8 on cosmology, Hubble's law, and the Einstein universe.

Discuss each problem and come to a group answer.

Let's work for 5 or so minutes.

The winners get chocolates.

See Solutions 30.

The de Sitter Universe

Willem de Sitter (1872--1934) presented the de Sitter universe (1917)---as we call it---in 1917 just after the Einstein universe (1917). The de Sitter universe (1917) is an expanding universe model with NO matter and only a cosmological constant tuned to give expansion. For an explication, see the figure below (local link / general link: willem_de_sitter.html).

Friedmann Equation (FE) Models

Alexander Friedmann (1888--1925) (see the figure below: local link / general link: alexander_friedmann.html) in Russia in the early 1920s and Georges Lemaitre (1894--1966) in Belgium just a bit later in the mid 1920s independently derived the Friedmann equation from which models of the universe can be obtained. These models can be called the Friedmann equation models or as a shorthand the FE models.

We elaborate on the Friedmann equation (FE) models below.

The Singularity:
FE models begin from a singularity of infinite density---with a couple of exceptions to be mentioned in subsection Avoiding the Singularity below.
The singularity was once called the POINT ORIGIN (Bo-85,181), but nowadays people are more likely to call it just the singularity or the Big Bang singularity.
For an image that can stand as a symbol for the Big Bang and the Big Bang singularity, see the figure below (local link / general link: big_bang_symbol.html).
How big is the
singularity in its theoretical context of taking the FE models as exactly true? Well if the universe is infinite, it's infinite or indeterminate. And if the universe if finite, it's a point.
But modern cosmologists do NOT think the singularity actually existed. Taking the FE models as exactly true at the singularity is pushing them beyond their validity since you reach infinite density. Infinities in physics usually mean that you have pushed a theory beyond its realm of validity. That seems likely to be the case for FE models at the singularity.
Nevertheless, the singularity is the time zero of the FE models: those that a have singularity that is. It is thought of as being approached, but NOT reached.
And the time of the singularity is still used as fiducial time zero of cosmic time with the understanding that it probably never happened. It is just beyond the limit of the time where we can extrapolate established physics which is the quark era (10**(-12) -- 10**(-6) s.
What happens instead of the singularity? Quantum gravity and perhaps other effects must supercede general relativity as infinite density is approached. We discuss the main ideas of what happened in section Inflation and Inflation Cosmology.
Avoiding the Singularity:
The FE models that have NO singularity and infinite age if their mass-energy is constant in time as they expand.
Such models are all it seems versions of the de Sitter universe (see section The de Sitter Universe above). A particularly famous version of the de Sitter universe is the famous steady state universe which had a vogue from the late 1940s to early 1960s when it was ruled out. We discuss the steady state universe in Appendix: The Steady State Universe (Not Required for the RHST).
Another way to avoid the singularity is to start a model from an Einstein universe. Recall the Einstein universe is unstable, and so the right kind of global perturbation will start it growing and it will evolve asymptotically to a de Sitter universe. Local contracting perturbations were thought of as perhaps being the origin of galaxies (Bo-120). This cosmological model is called Lemaitre-Eddington universe (see, e.g., Bo-84,85,117--121,159,175,180; No-527). It had a vogue circa 1925--1935 when it was favored by Arthur Eddington (1882--1944), but NOT by Georges Lemaitre (1894--1966) at least after circa 1931 (see, e.g., Bo-84,85,117--121,159,175,180; No-527).
Hereafter, for simplicity, we will mean a finite-age FE model with a singularity when we say FE model.
The Big Bang:
In modern Big Bang cosmology, the term Big Bang is generally taken to mean the era from time zero (i.e., Big Bang singularity) to about 20 minutes.
During this time, the light elements of the universe (hydrogen, deuterium, helium, and some lithium) are believed to have been synthesized in the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m).
We should emphasize that the Big Bang is NOT a pressure explosion where the kinetic energy comes from heat energy (CL-36) and pushes the mass-energy of the observable universe apart.
In a quasi Newtonian physics sense (which is sort of an approximation to the general relativity sense), a balance between kinetic energy and gravitational potential energy are initial conditions of the observable universe and the Friedmann equation dictates how the observable universe evolves given that balance.
The Density Parameter and the Space Geometry of the Friedmann Equation Models:
The space geometry of FE models is determined by the density parameter which has the symbol the capital Greek letter Ω and which is often just referred to as Omega. See the figure below (local link / general link: greek_letter_omega.html).
Omega is the ratio of the universal mean mass-energy density ρ to a critical density ρ_c (of mass-energy) which is a natural TIME-DEPENDENT parameter of the models:
Ω = ρ/ρ_c .
The possible geometries of the FE models are illustrated in the figure below (local link / general link: universe_geometry.html).
The Cosmic Scale Factor a(t):
What the Friedmann equation (FE) actually gives is the cosmic scale factor a(t), where t is cosmic time.
The cosmic scale factor determines the scaling up of the expanding universe according to the formula
r(t)=a(t)*r_0 ,
where r_0 is the physical distance at the present epoch in cosmic time (i.e., cosmic present t_0) between any two points participating in the mean expansion of the universe and which we call comoving distance and r(t) is the physical distance at general cosmic time t.
We note at a_0=a(t_0)=1:
1. For cosmic time past a(t) < 1.
2. For cosmic time present a(t) = 1.
3. For cosmic time future a(t) > 1.
Note that using cosmic present as defining time for a_0=1 is a convention. Other conventions are used, but a(t=present)=1. This makes a lot of sense: "our era in the expansion of the universe is the measure of all things" (Protagoras (c.490--c.420 BCE), apocryphal).
Note:
The upshot of the above is that the cosmic scale factor a(t) gives the relative scaling up of the universe.
The scaling up is illustrated in the animation in the figure below local link / general link: expanding_universe.html).
The Cosmic Scale Factor a(t) and the Evolution of FE Λ=0 models:
The figure below (local link / general link: cosmic_scale_factor_lambda_zero.html) illustrates how a(t), and thus how the expansion of the expanding universe, evolves with cosmic time in the three qualitatively distinct versions of the FE Λ=0 models.
The slope of the curves in the diagrams in the figure above (
local link / general link: cosmic_scale_factor_lambda_zero.html) is the rate of change of of a(t): i.e., recession velocity of distance a(t). Since the slope always decreases with cosmic time for cosmological constant (AKA Lambda, Λ) zero, the expansion continuously decelerates for the FE Λ=0 models.
The Ω < 1 and Ω = 1 versions expand forever (although always at a decreasing rate because of the deceleration) and the universe (or our pocket universe) will end in the Big Chill (AKA heat death of the universe) which we will discuss below in the section The Fate of the Universe According to the Λ-CDM Model.
In the Ω = 1 version, the slope of a(t) goes to zero asymptotically as cosmic time goes to infinity---so the universe comes to rest as cosmic time t → ∞ when a(t) = ∞.
If Ω > 1, then the universe (or pocket universe) will eventually recollapse and there will be a Big Crunch. See the cartoon animation of the Big Crunch in the figure below (local link / general link: big_crunch.html).
Since the Big Crunch is itself a singularity, we do NOT really know what happens then or later.
Some have imagined a
cyclic universe where the Big Crunch is the Big Bang of a subsequent epoch that is followed by another Big Crunch, and so on.
The cyclic universe as originally suggested has NOT lasted. There seems no way without ad hoc hypotheses to predict what happens as the universe passes through a Big Crunch.
But newer kinds of cyclic universe are thought to be viable: e.g., the ekpyrotic universe which we briefly discuss in the section Inflation and Inflation Cosmology.
The FE Λ=0 Models and Hubble's Work:
A KEY POINT is that the FE Λ=0 models predict either an expansion or a contraction of the universe: i.e., a(t) is never constant, but always changing.
This KEY POINT was made before Hubble observationally proved Hubble's law (see subsection Who Discovered the Expansion of the Universe and Hubble's Law? below).
Hubble's law itself is a consequence of the FE models (with Λ=0 or not). This was shown explicitly by Georges Lemaitre (1894--1966) in 1927 as we discuss below in subsection Who Discovered the Expansion of the Universe and Hubble's Law?. See Georges Lemaitre (1894--1966) again in the figure below (local link / general link: georges_lemaitre.html).
The FE Λ=0 models Do Not Tell US Everything:
The FE Λ=0 models in themselves do NOT tells us everything. In particular they do NOT tell us the values of the Hubble constant or Omega.
So they are certainly incomplete cosmological models.
In principle, the Hubble constant and Omega can be determined by observations, of course. In fact, they have been so determined to some accuracy.
How the Hubble constant is determined we have already discussed. How Omega is determined we will briefly mention below in the section The Accelerating Universe and the Friedmann equation Λ Models.
But the fact that the FE Λ=0 models predicted the expansion of the universe before that was observationally well established and Hubble's law probably before it was known to the person making the prediction (i.e., Lemaitre's) is very impressive.
The successful prediction of the expansion of the universe certainly did suggest that FE Λ=0 models could be right as far as they went.
Who Discovered the Expansion of the Universe and Hubble's Law? (Reading Only)
Now that we have discussed de Sitter universe and FE Λ=0 models, we are prepared to discuss this fine point of the history of astronomy. The figure below (local link / general link: georges_lemaitre_cartoon.html) gives the discussion.

Group Activity:

Form groups of 2 or 3---NOT more---and tackle Homework 30 problems 6--11 on cosmology and the FE Λ=0 models.

Discuss each problem and come to a group answer.

Let's work for 5 or so minutes.

The winners get chocolates.

See Solutions 30.

The Accelerating Universe and the Friedmann equation Λ Models

So the accelerating universe ...

How We Got Where We Are Now in Modern Cosmology:
How we got where we are now in modern cosmology with lots of omissions:
1. 1917: The static, hyperspherical Einstein universe with non-zero cosmological constant Λ which was invented to make the universe static (No-520; Bo-97).
2. 1917: The de Sitter universe developed by Willem de Sitter (1872--1934) (No-518,521; CL-28--29,159). This is zero-density, exponentially expanding universe. Historically, the de Sitter universe is of interest because it was the first model to predict universal expansion, but, of course, it was NOT right because it had NO matter. But nowadays, the de Sitter universe has been revived as a growth phase of the accelerating universe (see below in this section) and of inflation cosmology (see below in the section Inflation and Inflation Cosmology).
  See Astronomer file willem_de_sitter.html for more detail on the de Sitter universe.
3. 1917 to Mid-1960s: Various universe models including FE Λ=0 models, FE Λ≠0 models, and the steady state universe (which is actually a version of the de Sitter universe: see Appendix: The Steady State Universe (Not Required for the RHST)) had vogues for periods of time.
4. Circa 1965 to circa 1995--1998: In this period, FE Λ=0 models which were the standard cosmological models (with the discovery of the cosmic microwave background (CMB): e.g., No-541,560--563; Scott 2018). They predicted the expansion of the universe and their early dense phase allowed for the constituents of the observable universe to develop. The latter is a subject we discuss below in the section Big Bang Cosmology and the Initial Conditions of the Observable Universe.
  The most favored FE Λ=0 models was actually the Einstein-de Sitter universe (1932, standard model of cosmology c.1960s--c.1990s) which is NOT the Einstein universe (1917) NOR the de Sitter universe (1917). It is the simplest expanding universe FE model which is why Albert Einstein (1879--1955) and Willem de Sitter (1872--1934) proposed it (see Cormac O'Raifeartaigh, et al. 2015, arXiv:1503.08029). It has density parameter Ω=1 (and so has Euclidean geometry (AKA flat space geometry)) and cosmological constant zero (which is the same as NOT requiring the hypothesis of the cosmological constant). In proposing the Einstein-de Sitter universe (1932, standard model of cosmology c.1960s--c.1990s) in 1932, Albert Einstein (1879--1955) and Willem de Sitter (1872--1934) may have been trying to recapture the high ground from young upstart cosmologists: e.g., E.A. Milne (1896--1950), Georges Lemaitre (1894--1966), and William McCrea (1904--1999) (see also Wikipedia: E.A. Milne: Research into cosmology and relativity).
  However, the Λ-CDM model was actually already being considered as a possible cosmological model by circa 1995 based some evidence and other considerations even before the discovery of the acceleration of the universe (see Douglas Scot, 2018, arXiv:1804.01318 "The Standard Model of Cosmology: A Skeptic's Guide", p. 10).
5. 1998 on: In 1998 the first evidence appeared that the universal expansion was accelerating: to be more exact, positively accelerating unlike the FE Λ=0 models where the expansion is always negatively accelerating (i.e., decelerating).
The Acceleration:
The acceleration was first discovered by studying Type Ia supernovae.
These are very bright objects that can be seen using the modern giant telescopes to beyond 2500 Mpc (FK-649). Recall the current value for the Hubble length is 4283 Mpc / h_70, and so Type Ia supernovae can be seen to cosmologically large distances.
Their maximum luminosities are known reasonably well, and thus one can determine their luminosity distances from the inverse-square law for light: luminosity distances are NOT the same as cosmological physical distances (except in a static universe or approximately for very small cosmological physical distances), but they are DIRECT OBSERVABLES.
The cosmological redshifts of the parent galaxies of the Type Ia supernovae can be measured too.
Thus, one can determine a Hubble diagram for Type Ia supernovae.
Such diagrams extend to great distances with pretty high accuracy, and thus allowed a more sensitive test of Hubble's law and the nature of the expansion of the universe than before.
A representative Hubble diagram is shown in the figure below (local link / general link: hubble_diagram_4.html).
The
1998 Hubble diagram for Type Ia supernovae showed deviations from Hubble's law that could reasonably be fitted only if an acceleration of the expansion were assumed.
The deviations were NOT caused by peculiar velocities.
They are caused by the fact that redshift velocities and luminosity distances are NOT recession velocities and cosmological physical distances in general.
Redshift velocities and luminosity distances only approximate those quantities for the local universe.
Hubble's law is exact for recession velocities and cosmological physical distances in the FE Λ=0 models as aforementioned.
The Acceleration Becomes Established:
When the acceleration was first announced, people were somewhat skeptical.
The data had a lot of random errors---the deviations in plots from deceleration looked like pretty much like noise to my eye---and there could have been many systematic errors.
But since 1998, the data for Type Ia supernovae has continued to firm up and in addition 2 other independent evidences for acceleration have appeared.
To summarize without giving any details about how one knows:
1. The Type Ia supernova Hubble diagram directly points to acceleration.
2. Analysis of the cosmic microwave background radiation (CMB) (which we discuss below in the section Big Bang Cosmology and the Initial Conditions of the Observable Universe) strongly suggests that Omega=1.00±-0.02, but gravitational mass in galaxy clusters indicates Omega_matter=0.27±0.04 (FK-650,653).
  The missing mass-energy can be interpreted as some kind of dark energy that is powering the acceleration.
3. The integrated Sachs-Wolfe effect (CL-375) (which we won't go into) also points to acceleration.
So acceleration is rather well established: it still might be proven non-existent, but that would take a lot of counter-evidence now.
And if it was disproven would they have to take away the 2011 Nobel Prize in Physics for discovering the accelerating universe from my old pals shown in the figure below (local link / general link: adam_riess.html).
Explaining the Acceleration Theoretically:
How does one accommodate the acceleration theoretically?
Well the possibilities are quasi-endless.
But the simplest way is to fetch Einstein's cosmological constant Λ back from the storeroom of discarded theories and put it back in the Einstein field equations and the Friedmann equation, but now tune it to give the measured acceleration instead of a static Einstein universe.
One can then derive what one can call the FE Λ models which are just the FE models with the cosmological constant Λ NOT zero. The value of Λ is NOT determined by the model and must be determined by observational or other means.
The cartoon plot in the figure below (local link / general link: accelerating_universe.html) shows how the cosmic scale factor a(t) evolves an appropriate FE Λ model.
The increasing slope of the accelerating a(t) curve is the signature of acceleration.
Note that the accelerating model starts in a decelerating phase and then makes a transition to acceleration about 5 Gyr ago.
The transition to acceleration is less certain than the acceleration itself, but recent data for Type Ia supernovae suggest it (FK-650--651).

Dark Energy

We explicate dark energy in the insert entitled Lambda Λ: The Cosmological Constant and Dark Energy shown above in subsection The Introduction of the Cosmological Constant (see also: local link / general link: lambda_cosmological_constant_dark_energy.html).

The Λ-CDM Model

The Λ-CDM model (AKA concordance model) (as its alternative name suggests) is a concordance of several cosmological theories. Put together, these cosmological theories fit all cosmological observations of the observable universe to within uncertainty (except for a few tensions: see section Limitations and Tensions of our Current Cosmological Theories below) and with few relatively few free parameters thereby concording with Occam's razor too.

The name concordance model was once widely used, but has now fallen out of favor.

Note "Fit all all cosmological observations," EXCEPT for a few tensions (notably the Hubble tension since circa 2018) which we discuss below in section Limitations and Tensions of our Current Cosmological Theories.

So the Λ-CDM model may need some revision or even replacement as the standard model of cosmology (SMC).

For cartoon of cosmic cosmic history according to the Λ-CDM model and similar cosmological models, see the figure below (local link / general link: cosmos_history_2a.html).

The Ingredient Theories to the Λ-CDM model:
The ingredient cosmological theories are:
1. The FE Λ models with its free parameters fitted the modern data from Type Ia supernovae, the cosmic microwave background (CMB) (which we will discuss below in the section Big Bang Cosmology and the Initial Conditions of the Observable Universe), galaxy cluster observations, baryonic acoustic oscillations (BAOs), and other lesser observables.
  Most obviously, the fitted FE Λ model gives the expansion of the universe with positive acceleration: i.e., the accelerating universe.
2. Big Bang cosmology with its free parameters fitted to modern observations.
  Big Bang cosmology gives the cosmic microwave background (CMB) and the cosmic composition as we will discuss below in the section Big Bang Cosmology and the Initial Conditions of the Observable Universe).
  The Λ-CDM model is quantitative special case of Big Bang cosmology that may be right as far as it goes.
3. Cold dark matter (CDM) needed to give the large-scale structure of the universe.
  Cold dark matter is relatively slowly moving dark matter. We call it "cold" because it's moving at much less than the vacuum light speed c = 2.99792458*10**5 km/s ≅ 3*10**5 km/s.
  If the dark matter were moving at relativistic velocities in the early observable universe, it would NOT have been able to clump on relatively small scales under its self-gravity to form gravitational wells which are essential to the large-scale structure that we observe (see Wikipedia: Cold dark matter: Structure formation).
The Parameters of the Λ-CDM model:
Table: Cosmic Parameters below (local link / general link: cosmic_parameters.html) gives a representative set of values for the Λ-CDM model parameters.
We say "representative" because their is no single consensus set.
Various research groups using different analysis methods get slightly different sets and the parameter values will certainly change a bit more with future observations and analysis.
However, the differences among groups and with future work are likely to be less than 10 % or so.
The Cosmic Time Evolution of Some Important Λ-CDM model Cosmic Quantities:
The cosmic time of some important Λ-CDM model cosmic quantities is shown in the figure below (local link / general link: cosmic_scale_factor_lambda_cdm.html).
Comments on the Λ-CDM model:
Some comments on the Λ-CDM model are:
1. The many of the observations have gone into determining Λ-CDM model parameters are thought to be very accurate. But the uncertainties could be larger than is thought.
2. If the FE Λ models (of which the Λ-CDM model is a special case) are essentially wrong then derived quantities like the age of the universe and Omega might be wrong.
  If a model is wrong, then observations need to be interpreted in a different way.
3. And the Λ-CDM model may indeed need revision or replacement.
  Better observations could show inadequacy which, in fact, Hubble tension is suggesting right now (see section Limitations and Tensions of our Current Cosmological Theories below).
  One generally starts with the simplest adequate theory in obedience to Occam's razor with the understanding that more elaborate theories may be needed as observations advance.
  For example, a dynamical dark energy (i.e., a time-varying dark energy may be needed in a new standard model of cosmology (SMC).
4. The dark matter CANNOT be baryonic matter (i.e., ordinary matter of protons, neutrons, and electrons). may well be some strange, new exotic particle that interacts weakly with matter, except through gravity.
  The requirement for exotic dark matter is an inference as we will explain right now in brief.
  Big Bang nucleosynthesis (which discuss below in the subsection Big Bang Cosmology) predicts Omega_baryonic matter ∼ 0.045, and the Planck spacecraft (2009--2013) observations plus other data give Omega_matter at 0.3147(74) (Planck 2018 results. I. Overview and the cosmological legacy of Planck 2018)
  Big Bang nucleosynthesis is itself a very robust theory, and so we are forced to believe exotic dark matter is likely.
  There are many ideas about what the new particle may be. One favorite idea is WIMPs (weakly interacting massive particles). But the possibilities are still wide open.
  Anoher idea for dark matter is primordial black holes (PBHs) which we explicate in the figure below (local link / general link: black_hole_primordial.html).
  If we ever discover what the dark matter is, it will have profound implications for cosmology and fundamental physics.
5. Recall there is a counter theory to dark matter: MOND (MOdified Newtonian Dynamics which is explicated in the figure below (local link / general link: gravity_mond.html).
  If MOND turns out to be at all right, then the need for exotic dark matter may vanish and all of cosmology would be affected in radical ways.
6. Most of the ordinary matter (i.e., matter made of protons, neutrons, and electrons) is nearly invisible and we call it is sometimes called baryonic dark matter.
  However, we know what is: the intergalactic medium (IGM) and the a href="https://en.wikipedia.org/wiki/Intracluster_medium">intracluster medium Baryonic dark matter is usually NOT included in dark matter, but sometimes it is. Context usually must decide what is meant.
  We explicate baryonic dark matter just below in subsection Baryonic Dark Matter.
Where is the Baryonic Matter?:
Besides dark matter, there is also baryonic matter (i.e., ordinary matter made up of protons, neutrons, and electrons).
In fact, the Λ-CDM model fit to observations plus Big Bang nucleosynthesis (see below subsection Big Bang Nucleosynthesis) imply that baryonic matter is only ∼ 1/6 ≅ 16 % of all matter, the rest being dark matter (Ci-27).
Where is this baryonic matter? As a percentage of all baryonic matter:
1. intergalactic medium (IGM): ∼ 50 %.
2. circumgalactic medium (CGM): ∼ 40 %.
3. intracluster medium (ICM): ∼ 4 %.
4. baryonic matter in galaxies: stars, interstellar medium (ISM), white dwarfs substellar objects, neutron star, and black holes: ∼ 6 %.
Reference Ci-192.
So the intergalactic medium (IGM) (for brevity counting all of the IGM, CGM, and ICM as IGM) is estimated to be ∼ 94 % of the baryonic matter (i.e., ∼ 15 % of all matter), whereas baryonic matter in galaxies as (for brevity in stars if you know what you mean) is estimated to be only ∼ 6 % of baryonic matter (i.e., ∼ 1 % of all matter).
The upshot is that overwhelmingly most baryonic matter is the IGM, NOT in galaxies.
In fact, IGM has very low density, but there in a lot of volume in intergalactic space which compensates. The IGM is rather invisible because it is often very hot and so radiaties only a little in the X-ray band (fiducial range 0.1--100 Å). Shock heating heats the gas and it cools very slowly. For more on the heating of the IGM, see below subsection The Heating of the Intergalactic Medium.
Much of the IGM has the primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7) since it has been only a little polluted by outflows of metal-enriched gas from galaxies.
In fact, though you CANNOT easily deduce it from the values above, the baryon fraction (i.e., baryonic mass over total mass) in galaxies is rather low ⪅ 3 %, whereas in the IGM it is nearly the universal value of ∼ 16 %. This lowness is called the missing baryon problem. Somehow galaxies are rather good at expelling baryonic matter. There are possible solutions to the missing baryon problem (Ci-191--194), but they are beyond our scope to go into.
The mass-energy contents of the observable universe are further discussed in the figure below (local link / general link: pie_chart_cosmic_energy.html).
The values in the figure are somewhat different than those discussed above. This is because different references always give different values due difference in estimation procedures.
The Heating of the Intergalactic Medium (Reading Only):
subsection UNDER RECONSTRUCTION

As discussed above in subsection Where is the Baryonic Matter?, most of the baryonic matter in the observable universe is in the intergalactic medium (IGM) (for brevity counting all of the intergalactic medium (IGM), Circumgalactic medium (CGM), and intracluster medium (ICM) as IGM).
Also as discussed above in subsection Where is the Baryonic Matter?, most of the IGM is rather hot.
Why?
The theory is that the gas falls into galaxy superclusters, galaxy clusters from voids and gravitational potential energy gets converted to heat energy. The gas is then the warm-hot intergalactic medium (WHIM) (i.e., ionized H and He gas with temperatures in range 10**5--10**7 K) along with somewhat warmer and colder gas.
Shocks from galaxy collisions and outflows from active galaxies give more heating. Some heat energy may be left from the original phase of galaxy formation. WHIM cools very slowly.
WHIM is almost invisible because it emits low energy X-rays (which are mostly drowned out by Milky Way X-ray emission) and extreme ultraviolet light to which the neutral Milky Way hydrogen is opaque (CO-3).
We have observed WHIM and yours truly thinks it is now established that WHIM is most of the baryonic dark matter.
Eventually, maybe in several Hubble times, some of the WHIM will be cooled enough to collapse into new galaxies (CO-5). This would keep star formation going in the universe for some time. But the continued and accelerated expansion of the universe might prevent all of it from collapsing????.

Group Activity:

Form groups of 2 or 3---NOT more---and tackle Homework 30 problems 9--15 on cosmology, FE Λ=0 models, and the Λ-CDM model.

Discuss each problem and come to a group answer.

Let's work for 5 or so minutes.

The winners get chocolates.

See Solutions 30.

Cosmological Distance Measures Explained (Reading Only)

Now that we have covered the Λ-CDM model, a recapitulation of the explication of the cosmological distance measures is useful. See the figure below (local link / general link: cosmos_distance_z_10000.html).

The Fate of the Universe According to the Λ-CDM Model

The fate according to Frost---see figure below (local link / general link: robert_frost.html).

What is the fate of the universe Λ-CDM model is taken as absolutely correct for the universe---or, if the multiverse exists, our pocket universe---but we won't reiterate that qualification to avoid tediousness.

In other words, what is the Λ-CDM-model cosmic future.

A highly speculative sketch---which gets more speculative as it goes along---is as follows (HI-477, Wikipedia: Graphical timeline from Big Bang to Heat Death, Wikipedia: Future of the expanding universe):

Where We are Right Now: Cosmic Time t≅ 10**10 Years:
Currently, we are at cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018): i.e., at cosmic time = age of the observable universe = 13.797(23) Gyr (Planck 2018) ≅ 10**10 years counting from the Big Bang.
End of the Stelliferous Era: Cosmic Time t≅ 10**14 Years:
At cosmic time of order 10**14 years (∼ 10,000 times the current cosmic time), all star formation will have ended and all the long-lived M stars will have left the main sequence???. See the figure below (local link / general link: star_lifetimes.html).
This is the end of the
Stelliferous Era (i.e., the star-making era).
The universe will consist of mainly of dark matter particles (probably and assuming dark matter is NOT primordial black holes (PBHs)), compact remnants (i.e., white dwarfs, neutron stars, and black holes), and uncollapsable H and He gas???.
Why does star formation turn off?
Well, a significant fraction of the baryonic matter (still mainly primordial hydrogen and helium gas) of the observable universe will have been turned into compact remnants, and will thus be unavailable for new star formation. This is probably the fate for baryonic matter trapped or still to become trapped in large gravitational wells.???
But the main reason??? is that the continued expansion of the universe (which recall is an accelerating expansion of the universe) will spread the intergalactic medium (IGM) (still mainly primordial hydrogen and helium gas plus dark matter) so much that it is uncollapsable into significant gravitational wells.
No more runaway gravitational collapses. No more star formation.
Proton Decay Era: Cosmic Time t≅ 10**31 to 10**36 Years:
It is possible for quantum field theory reasons that protons radioactively decay (and this entails the radioactive decay of neutrons too) into electrons, positrons, neutrinos, and photons with a half-life of something in the range 10**31 to 10**36 years (see Wikipedia: Proton decay). Note there is NO experimental evidence for proton decay so far.
Assuming proton decay, at some cosmic time in excess of 10**31 years, the protons and neutrons will have all decayed. This will leave a dilute gas of electrons, positrons, neutrinos, and photons, and dark matter particles, and black holes.
Actually, dark matter particles may undergo spontaneous radioactive decay to Standard Model particles though there is NO accepted time scale (Wikipedia: Dark matter: Indirect detection).
For a dilute gas of photons, etc. in the heat death of the universe (which we discuss below in subsection The Heat Death of the Universe: Cosmic Time t >> 10**100 Years, see the figure below (local link / general link: heat_death_photons.html).
End of Black Hole Era: Cosmic Time t≅ 10**100 Years:
Black holes are theorized to evaporate by Hawking radiation.
By a cosmic time of order 10**100 years, the black holes may have evaporated and the vastly expanded universe could be only a very dim, dilute gas of electrons, positrons, neutrinos, photons, and dark matter particles---if they have NOT undergone spontaneous radioactive decay to Standard Model particles (Wikipedia: Dark matter: Indirect detection).
Some hypothetical dark matter particles decay to baryonic matter with very long half-lives (see Wikipedia: Dark matter: Indirect detection). So maybe the dark matter particles will be gone too by of order 10**100 years ??? in the Λ-CDM-model cosmic future.
The Heat Death of the Universe: Cosmic Time t >> 10**100 Years:
The expanding universe is now cold and dark and getting more so as the expansion continues---this is the heat death of the universe which was first discussed by William Thomson, Lord Kelvin (1824--1907) shown in the figure below (local link / general link: lord_kelvin.html).
See the image of photon gas in darkness in the figure above (local link / general link: heat_death_photons.html) in the figure below (local link / general link: lord_kelvin.html).
So the universe ends in ice metaphorically speaking---according to the Λ-CDM-model cosmic future.
The Wild Extrapolation:
The heat death of the universe as just described is the end of the story according to the Λ-CDM model---but there's NO reason to put much faith in it---it's a very speculative story.
It is, in fact, a wild extrapolation of the Λ-CDM model well beyond the observations it is fitted to. So it would NOT be surprising if the story got more and more wrong, the further in cosmic time it is extrapolated---but we may never know. See our story in the figure below (local link / general link: mayfly.html).
The Tensions with the Λ-CDM Model:
Recall, there are some tensions with the Λ-CDM model which we discuss in detail in section Limitations and Tensions of our Current Cosmological Theories. These could lead to a revision or replacement of the Λ-CDM model by a new standard model of cosmology (SMC).
With a new standard model of cosmology (SMC), we might have new wild extrapolation story for the far future.

Big Bang Cosmology and the Initial Conditions of the Observable Universe

Big Bang cosmology is the super theory or paradigm (i.e., overall grand theory) of which Λ-CDM model is a particular quantitative version. It would very, very probably survive if the Λ-CDM model were discarded.

For an image that can stand as a symbol for the Big Bang and the Big Bang singularity, see the figure below (local link / general link: big_bang_symbol.html).

Among other things, Big Bang cosmology sets the initial conditions for the FE Λ models (and other kinds of cosmological models too) and the large-scale structure of the universe.

So it is the explanation of the initial conditions of the observable universe (or of our pocket universe in the eternal inflation version of the multiverse paradigm).

In common modern usage, Big Bang means the early hot, dense phase of the observable universe.

The initial conditions set by the Big Bang are the primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7), the cosmic background radiation (CBR) (which is what turned into the cosmic microwave background radiation (CMB, temperature T = 2.72548(57) K (Fixsen 2009))), and the small fluctuations from perfect homogeneity in mass-energy density that were the seeds for the evolving large-scale structure of the universe.

perfect fluid

cosmological substratum

mass-energy

universe

FE Λ models

We explicate Big Bang cosmology below:

Primeval Atom Theory:
The ancestor of Big Bang cosmology for the constituents of the observable universe was Georges Lemaitre's (1894--1966) primeval atom theory (1933)---but we won't discuss in detail that historically interesting, but long discarded, theory (No-530). See young Lemaitre (1894--1966) hanging out with the old guys in the figure below (local link / general link: georges_lemaitre.html).
In brief, the primeval atom theory posited a cold "Big Bang" in which a giant mass of neutrons (i.e., the primeval atom itself) filling a small positive curvature universe (a hyperspherical universe: finite, but unbounded). This small universe expanded according to a FE Λ≠0 model which we call the Lemaitre universe (1933). The primeval atom fragmented into smaller and smaller fragments of which the smallest are the hydrogen (H) helium (He). Larger fragments continue to exist and some are radioactive isotopes. These radioactive isotopes are inside stars and planets undergo radioactive decay: they power stars and provide radiogenic heat in planets.
The primeval atom theory (1933) was a brilliant theory and was viable circa in the 1930s. However, advances in nuclear physics and in the understanding of hydrogen burning in stars by the middle 1940s made it seem implausible and effectively ruled it out. Georges Lemaitre (1894--1966) himself continued to discuss the primeval atom theory (1933) in his later years while admitting he had become and old-fashioned cosmologist???.
The Big Bang:
In the 1940s (by which time nuclear physics was much more elucidated than in the 1930s), George Gamow (1904-1968) (see figure below local link / general link: george_gamow.html), Ralph Alpher (1921--2007), and Robert Hermann (1914--1997) worked out an early version of Big Bang nucleosynthesis (No-531ff, 559ff): the theory that the elements were synthesized by nuclear fusion from hydrogen nuclei in an early hot, dense phase of the universal expansion: i.e., in the Big Bang in the primary meaning of the term.
Originally,
Gamow et al. tried to show that all the nuclei could have been formed in this early phase (Bo-58), but later this turned out to be impossible it seems (No-560). The heavier nuclei are mostly accounted for by nucleosynthesis in stars followed by ejection by stellar winds and in supernovae where they thrown out into space by the supernova explosion itself (No-540).
But stars CANNOT account for the light elements: hydrogen (H-1), deuterium (H-2), helium (He-4 and He-3), and lithium (Li-7 and Li-6) (see Wikipedia: Big Bang nucleosynthesis).
The case for He is particularly acute: there seems far too much to have been produced in stars.
Recall the cosmic composition by mass is about the same as the solar composition: see below Table: Cosmic Composition (local link / general link: cosmic_composition_table.html).
The aforesaid light elements are accounted for by Big Bang nucleosynthesis. See Table: Cosmic Composition in the insert below (local link / general link: cosmic_composition_table.html).
The Initial Conditions of the Big Bang:
The idea is to start cosmic time at some early hot, dense phase of the universe with some simple primordial constituents and then run the clock forward synthesizing the nuclei as space expands and cools. The gas expands with space and this cools it by a commonplace physical effect: adiabatic cooling---which we won't go into, but its everywhere including everyday life.
We CANNOT start the clock at the TIME ZERO of the Friedmann equation (FE) models since then there is infinite density (i.e., the Big Bang singularity) and general relativity must fail before that state is reached: we need a theory of quantum gravity to go the realm of super high densities and we do NOT have an established one (CL-122).
In fact, before about one Planck time (t_Planck ≅ 5*10**(-44) s) when density is very high our theories are very speculative. This period is called the Planck era.
The very earliest times before a second or so are in also in speculative realm (thought NOT as speculative as the Planck era) where the matter is believed to be so hot and dense that only quarks and leptons (the most familiar of which is the electron) and their antiparticles exist and in which matter and antimatter are about equal in abundance (FK-668).
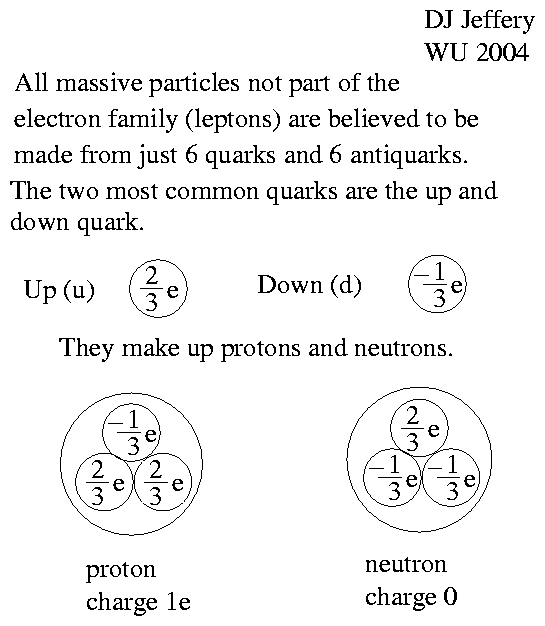
For how quarks make up protons and neutrons, see the figure below.
Free quarks exist only under super-dense conditions. If you try to pull apart composite particles (e.g., protons) made up of quarks under less dense conditions, new quarks come into existence to make new composite particles.
The energy from the pulling apart goes into making the new composite particles.
Leptons are electrons, positrons (antielectrons), neutrinos, and some less common species.
Matter and antimatter mutually annihilate to produce photons.
The mutual annihilation destroys the antimatter and leaves a trace of matter.
It is thought in theories of particles that there is some asymmetry in properties between matter and antimatter that slightly favors matter (FK-668).
The usual assumption is that the early universe is isotropic and very homogeneous: i.e., among other things has nearly constant temperature, density, and composition at any given cosmic time.
There are small density fluctuations that will be the seeds of the large-scale structure that will form in of order the first billion years. Gravitational runaways will start from the seeds.
The continuous expansion causes the temperature and density to fall steadily. Recall the cooling is just due to adiabatic expansion.
The evolution of the cosmic temperature during cosmic time 10**(-10) s -- 10**16 s ≅ 0.3 Gyr which includes the early universe (10**(-12) s -- 380,000 y) is shown in the figure below (local link / general link: cosmic_temperature.html).
The Timeline of the Big Bang in Snapshots:
We will just give a simple presentation of the timeline of the early universe in a sequence of snapshots.
The captions are subject to revision from time to time, and so should NOT be taken as definitive.
The dark matter particles were omitted from the figures, but they should be assumed to be there too.
The snapshots:
1. Caption: electroweak era (t ∼ 10**(-36)s to quark era (t ∼ 10**(-12)s.
  At the electroweak era (t ∼ 10**(-36)s the strong nuclear force may have become distinct from the weak nuclear force and electromagnetic force which were still united as the electroweak force: i.e., the two acted in the same way. This era may have been just before inflation (see Wikipedia: Electroweak epoch.
  The dark matter particles were omitted from this and following figures, but they should be assumed to be there too.
  Credit/Permission: © David Jeffery, 2004 / Own work.
  Image link: Itself.
2. Caption: Early universe 1: Lepton era (t ∼ 1 s).
  Credit/Permission: © David Jeffery, 2004 / Own work.
  Image link: Itself.
3. Caption: Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m).
  This was once thought to be about 3 minutes and hence the famous book The First Three Minutes, Steven Weinberg, 1977.
  Credit/Permission: © David Jeffery, 2004 / Own work.
  Image link: Itself.
4. Caption: recombination era t = 377,770(3200) y.
  Credit/Permission: © David Jeffery, 2004 / Own work.
  Image link: Itself.
5. Caption: Early universe 5: cosmic time t ≅ 1 Gyr.
  Circa 2023, early results from James Webb Space Telescope (JWST, 2021--2041?) suggest that galaxies may have formed as early as cosmic time t ≅ 0.35 Gyr (see J. O'Callaghan, 2022 Dec06, SciAm, "Astronomers Grapple with JWST’s Discovery of Early Galaxies"). If this result is confirmed, it may be another tension for the Λ-CDM model.
  Credit/Permission: © David Jeffery, 2004 / Own work.
  Image link: Itself.
After snapshot 5, the universe (or pocket universe) continues to evolve to cosmic present t_0 = to the age of the observable universe = 13.797(23) Gyr (Planck 2018).
The Recombination Era:
The recombination era is when the electrons and nuclei combine to form NEUTRAL atoms: mainly hydrogen and helium, of course.
The NEUTRAL atoms have much lower cross sections for interactions with photons of the temperature of the recombination era of about 3000 K (FK-670).
The lower cross sections of NEUTRAL atoms are such that after about the recombination era, the matter in the universe (or pocket universe) becomes largely transparent to the primordial photons after the recombination era.
Before the recombination era, the photons interacted strongly with matter and thus matter and photons were held at the same temperature. At recombination itself this temperature was ∼ 3000 K as noted above.
After recombination era the primordial photons (i.e., cosmic background radiation) streamed off through space only slightly interacting with matter again.
The photons just after the recombination era had a blackbody spectrum at ∼ 3000 K and which according to Wien's law peaked in the near infrared (roughly 0.75--1.4 μm) at ∼ 1 μm. This cosmic photon gas for all eras is called the cosmic background radiation.
The primordial photons of the cosmic background radiation after the recombination era stream mostly freely through space. They do interact a little, of course: they can scatter off free electrons in space, run into stars and planet, be affected by gravitational effects, and other lesser interactions.
The primordial photons cool by expansion of the universe. Their wavelengths scale with the cosmic scale factor a(t) and their density decreases as the volumes scale up.
In fact, it can be shown that primordial photon distribution remains blackbody-like with a constantly decreasing temperature due to expansion.
In 1949, Alpher and Hermann predicted the present-day temperature of the cosmic background radiation would be ∼ 5 K (No-559). Actually, Alpher and Hermann's calculation was rather defective and they only fortuitiously got a temperature of order of the current value for the cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009)) (see Mike Turner 2021, Predicting the CMB temperature).
Using Wien's law
```
          2897.7685(51) μm*K
  λ_max = ------------------ ≅ 600 microns = 0.06 cm
              (T = 5 K) 
```
which by common definition is long wavelength infrared (HZ-54; FK-94). But the microwave band is redward of 0.1 cm where much of the primordial photon spectrum is.
The cosmic time of evolution of the temperature of the cosmic background radiation form well after the Big Bang nucleosynthesis (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) and starting well into the radiation era (cosmic time ∼ 0--178.5 kyr) is shown in the figure below (local link / general link: cosmic_scale_factor_lambda_cdm.html).
The Cosmic Microwave Background (CMB):
The relic primordial photon gas (i.e., the cosmic background radiation) in the modern observable universe is called the cosmic microwave background radiation (CMB).
In 1965, Arno Penzias (1933--2024) and Robert Wilson (1936--) (see the figure below: local link / general link: arno_penzias.html) working with a Bell Labs radio telescope in Holmdel Township, New Jersey fortuitously discovered cosmic microwave background radiation (CMB, blackbody temperature T = 2.72548(57) K (Fixsen 2009)), but at only wavelength 7.3 cm in the microwave band (fiducial range 0.1--100 cm, 0.01--10 cm**(-1)). The CMB is a nearly uniform radiation field coming to us from all directions.
Penzias and Wilson got the 1978 Nobel Prize in Physics for their discovery; Alpher and Hermann did NOT get a Nobel Prize.
The CMB is best measured from space, because the Earth's atmosphere is opaque to much of the spectrum of the CMB.
The first highly accurate CMB measurement over a broad wavelength range was reported from the COBE spacecraft circa 1990 (FK-640). The CMB sprectrum with data points from many observation devices is shown in the figure below (local link / general link: cmb_2.html).
The CMB Dipole Anisotropy (Reading Only):
The CMB has a large-scale variation (called the CMB dipole anisotropy) caused by the Earth's peculiar velocity with respect to the local inertial frame participating in the mean expansion of the universe (FK-640--641).
The Solar System's peculiar velocity with respect to the local inertial frame is, in fact, best known from the CMB dipole anisotropy.
The motion is 371 km/s in the direction of Leo and away from Aquarius (FK-640--641).
We can deduce that the Local Group of galaxies is moving at 620 km/s relative to the local inertial frame in the direction the Hydra-Centaurus Supercluster (FK-640--641).
The CMB Fluctuations:
If the CMB dipole anisotropy is subtracted, there remain small-scale random fluctuations in CMB temperature of order 200 micro-Kelvins or in relative terms of 1 part in 10**5 (Wikipedia: Cosmic microwave background: Features). These fluctuations are formally called the CMB primary anisotropy.
The CMB temperature fluctuations (shown in the figure below local link / general link: cmb_wmap.html) are believed to correspond to primordial density fluctuations that were the seeds for the gravitational collapses that led to the formation of the galaxies and the large-scale structure (see IAL 28: Galaxies).
Big Bang Nucleosynthesis:
To return to the cosmic abundances of the elements and Big Bang nucleosynthesis.
Modern Big Bang nucleosynthesis depends on the parameter the primordial baryon-to-photon ratio η which is of order 10**(-9). The best value is maybe 6.1*10**(-10) (see "Best" Cosmological Parameters, 2003). In this context, the baryons are overwhelmingly just protons and neutrons.
The baryon-to-photon ratio η is an adjustable free parameter of the calculations.
The WMAP measurements of the CMB and observed primordial deuteron abundance actually give a value for this ratio of (6.13±0.25)*10**(-10). (Spergel, D. N. et al. 2003, ApJ, astro-ph/0302209, First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters; Mathews, G. J., et al. 2004, Phys. Rev. D, submitted, astro-ph/0408523, Big Bang Nucleosynthesis with a New Neutron Lifetime).
With the ratio parameter set to this value, the predictions of calculations of Big Bang nucleosynthesis can be compared with measured light elements corrected for stellar nucleosynthesis effects where possible.
The comparison yields very favorable agreement, in fact.
But also it sets a limit on the density of baryonic matter (including the baryonic dark matter) in the observable universe. This limits only ∼ 1/6 of the dark matter needed to explain galaxies and galaxy clusters.
The upshot is that the dark matter is NOT baryonic matter. It is usually though to be an exotic dark matter particle, but maybe it is primordial black holes.
We illustrate Big Bang nucleosynthesis and the comparison with observed cosmic composition in the figure below (local link / general link: big_bang_nucleosynthesis.html).
Summary of the Strongest Evidence for Big Bang Cosmology:
Let us summarize the strongest evidence for Big Bang cosmology:
1. The observed expansion of the universe is predicted. This was done before it was observed.
2. The observed CMB is predicted naturally as the relic of the hot early universe (or our hot early pocket universe). This was also done before it was observed.
3. The observed light element abundances are well predicted.
4. The observed large-scale structure can be explained as having been seeded by the primordial density fluctuations that manifest themselves in CMB fluctuations.
  Calculations starting from the primordial fluctuations and using many assumptions especially about the dark matter do seem to be reproducing the observed large-scale structure though a lot of uncertainty remains (FK-671ff).
5. The oldest stars whose age we can well determine by modeling are in Milky Way globular clusters. The modeling is subject to some uncertainties, but has improved greatly since it began in the 1950s. The ages are of order 12.5±1.0 Gyr (FK-638).
  These ages are less than the age of the observable universe = 13.797(23) Gyr (Planck 2018) given by the Λ-CDM model (FK-653).
  At present, there is no problem with contents of the universe being older than the Big Bang cosmology predicted age of the universe which in the past has occasionally been an embarrassment (Bo-39,51--52).
At present, there are NO viable rivals to Big Bang cosmology.
And this has really been so since the 1960s despite the attempts of mavericks like Fred Hoyle (1915--2000) to present viable alternatives.
The alternatives have always had many ad hoc and/or complicating assumptions.
These assumptions are mostly fix-ups to try to explain things that Big Bang cosmology explains in a natural way.
Big Bang cosmology is a very robust theory nowadays.
It would be astonishing if it turned out to be just plain WRONG.
It is probably right as far as it goes.
But Big Bang cosmology does NOT tells us what happened before the Big Bang for example.
We take take up the limitations of the Λ-CDM model (which incorporates Big Bang cosmology) in the following section Limitations of the Λ-CDM Model.

Limitations and Tensions of our Current Cosmological Theories

Our current cosmological theories have limitations and tensions as explained in the insert below (local link / general link: big_bang_cosmology_limitations.html).

Inflation and Inflation Cosmology

The relevance will emerge below of the quote from Hamlet (c. 1601) (see the figure above local link / general link: hamlet_edwin_booth.html).

The Inflation Paradigm:
Inflation is the name for a super-rapid exponential expansion phase (cosmic time maybe 10**(-36)--10**(-33) or 10**(-32) s measured from the fiducial time zero of Friedmann equation (FE) models) from a tiny piece of space that may have happened in the very early universe (cosmic time t ⪅ 10**(-12) s). The expansion is much more rapid than in the (post-very-early-universe) FE models (i.e., a model with "radiation", "matter", and the cosmological constant Λ (or some more complicated form dark energy).
After inflation, the cosmic evolution is supposed to track into one of these FE models.
The term inflation is also used in a broader sense to mean inflation cosmology and the inflation paradigm. These three terms can all be considered synonyms in many contexts.
To explicate paradigm: it is a term in the jargon of philosopher of science Thomas Kuhn (1922--1996). It is grand overall theory into which many other theories fall. You could also call it a framework for many theories.
So inflation is NOT a single well-defined theory.
There tens of inflation theories: i.e., versions of inflation.
We do NOT know which if any are correct NOR whether inflation is correct.
But inflation has staying power since it's been around since 1979 (see Wikipedia: Inflation: History) and remains the leading paradigm for the origin of the observable universe and perhaps it is the correct paradigm for the whole universe throughout eternal space and time.
Inflation and other versions of quantum cosmology are embedded in the grander paradigm of quantum field theory.
The inflation paradigm is further explicated in the figure below (local link / general link: inflation_paradigm.html).
The History of Inflaton:
The idea of inflation was developed independently by Alexei Starobinsky (1948--) in Russia and Alan Guth (1947--) in the US in 1979--1980. Guth also coined the term inflation (Wikipedia: Inflation: History). For Alan Guth (1947--), see the figure below (local link / general link: alan_guth.html).
Inflation is, in fact, a paradigm as discussed above in section The Inflation Paradigm. Within the inflation paradigm, a seemingly unlimited number of particular inflation theories can be developed.
Since 1979, the inflation paradigm has evolved quite a bit and has indeed spawned a quasi-infinity of inflation theories.
Among these inflation theories is eternal inflation which, in fact, has many versions itself. We discuss eternal inflation below in subsection Eternal Inflation.
The main developer of the theory of eternal inflation is Andrei Linde (1948--): see the figure below (local link / general link: andrei_linde.html).
Three Problems Solved by Inflation:
Inflation was and is considered a good idea just because it offers explanations for 3 problems.
The 3 problems are:
1. The Magnetic Monopole Problem:
  Alan Guth's (1947--) original reason for developing inflation was to solve the magnetic-monopole problem. Magnetic monopoles are isolated magnetic poles: we ordinarily always see magnetic dipoles: there is always and north and south pole.
  The problem is one that particle physicists created for themselves. Grand unified theories (GUTs), which unite the strong nuclear force, weak nuclear force, and electromagnetic force, seem to predict that magnetic monopoles should be created in the very early universe (cosmic time t ⪅ 10**(-12) s) (or maybe a somewhat later???) and be as common as protons and be much more massive (Ov-239--240). But none are observed and they havn't caused a rapid recollapse of the universe ???.
  A phase of inflation would decrease the magnetic-monopole density to practically unobservable: Alan Guth originally estimated about one MAGNETIC MONOPOLE in the observable universe (Ov-245).
  Problem solved---if it ever really existed.
  However, even if the magnetic-monopole problem turns out to be a myth, it was useful in furthering research in cosmology.
2. The Horizon Problem:
  The temperature of CMB is extremely uniform. It shows fluctuations of only about 1 in 10**5 (see Wikipedia: Cosmic microwave background radiation: Features) after subtracting off the cosmic microwave background (CMB) dipole due to the Doppler effect caused by the Earth's motion relative to the comoving cosmic rest frame. (See the discussion of the comoving cosmic rest frame in at frame_basics.html#comoving frames.)
  The extreme uniformity implies that the whole early universe (cosmic time (10**(-12) s -- 377700(3200) Jyr) before the recombination era t = 377,770(3200) Jyr = 1.192*10**13 s (z = 1089.80(21)) was very homogeneous and in very nearly in exact thermodynamic equilibrium (i.e., at nearly the same temperature).
  But in FE models with a Big Bang, points on opposite sides of sky from which CMB flux originated were never CAUSALLY CONNECTED (except perhaps in a limiting sense at that the physically indeterminate and very probably unreal Big-Bang singularity itself).
  Those points were NOT within each other's observable universes.
  So how could the early universe have such a uniform temperature if it never had a chance to thermally equilibrate?
  More generally how could the early universe be so homogeneous?
  This is the horizon problem---which is explicated in the figure below (local link / general link: inflation_horizon_problem.html).
3. The Flatness Problem:
  The observable universe has Omega very close to 1: the probably the best current measurements give |Omega -1| = 0.0005(40) (which is consistent with zero within 1 standard deviation (1 σ)) for cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018) (Planck 2018 results. I. Overview and the cosmological legacy of Planck 2018, p. 31).
  Recall Omega = 1 means the observable universe is flat: i.e., has Euclidean geometry (AKA flat space geometry).
  In Friedmann equation Λ=0 models, the density parameter Ω(t) (i.e., Omega as a function of cosmic time) always diverges from 1, unless it is exactly 1. In other words, Omega = 1 is an unstable state.
  So a very flat observable universe at cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018) means the observable universe was very flat in earlier times.
  But why was it so flat? This is the flatness problem.
  The flatness problem and how inflation paradigm solves it are explicated in the figure below (local link / general link: inflation_flatness_problem.html).
4. Conclusion of the Three Problems:
  So we see that inflation paradigm offers solutions to three problems that physicists have with the standard Big Bang cosmology.
  These solutions are general to all reasonable versions of inflation.
Is there More Evidence for the Inflation Paradigm?
Yes, from the fact that the Cosmic microwave background (CMB) power spectrum is a scale-invariant power spectrum. For an explication, see the figure below (local link / general link: cmb_power_spectrum.html).
The Problem with the Inflation Paradigm:
A main problem with the inflation paradigm is that there are tens of different versions of inflation.
As aforesaid in subsection The Inflation Paradigm, we do NOT know which if any are correct NOR whether the inflation paradigm is correct.
Some versions have been ruled out, of course, but new ones keep appearing.
What can we say in favor of the inflation paradigm?
The physics of the inflation paradigm (discussed in the figure above: local link / general link: inflation_eternal.html) seems a good idea to quantum field theorists and the inflation paradigm solves three significant problems as discussed above in subsection Three Problems Solved by Inflation. But these features are generic. All reasonable versions of inflation have them.
Also, as discussed above in subsection The Inflation Paradigm, the inflation paradigm has staying power. It's been around since 1979 (see Wikipedia: Inflation: History) and remains the leading paradigm for the origin of the observable universe and perhaps it is the correct paradigm for the whole universe throughout eternal space and time.
However, the fact that inflation paradigm has failed to generate a single established version is a reason to continue to challenge it.
In fact, yours truly like many others still considers it a speculative theory.
Eternal Inflation:
Here yours truly will only vaguely sketch what is called eternal inflation based largely on combination of FK-661--667, Gr-272--323, and Carroll, S., & Chen, J. 2004 Spontaneous Inflation and the Origin of the Arrow of Time (hereafter SC).
Eternal inflation is itself a paradigm with many versions.
The reason for discussing it is just it is the paradigm that many astronomers (including yours truly) think in terms of while still regarding it as speculative. If the inflation paradigm itself is true, eternal inflation just seems to be the most reasonble generalization of it since eternal inflation tells us where the observable universe fits into the whole universe. Eternal inflation just gives us answers to questions that the minimal inflation paradigm does NOT give.
Eternal inflation posits a multiverse consisting of a background universe which is exactly the false-vacuum universe discussed in the figure above (local link / general link: inflation_paradigm.html).
However, going beyond the minimal inflation paradigm, the false-vacuum universe has infinitely many pocket universes embedded in it that all grew at some time from inflation regions. The observable universe is embedded in one of these pocket universes: i.e., in our pocket universe.
Where do the pocket universes come from? Just as in the minimal inflation paradigm, a random quantum fluctuation (and random quantum fluctuations are a fundamental feature of quantum mechanics and quantum field theory) pushes an inflation region in the false vacuum universe over an energy threshold and the inflation region transitions to the quantum vacuum state by undergoing inflation super rapid exponential expansion. The inflated inflation region is a pocket universe.
So a mighty oak grows from an acorn---and this was the nutshell Hamlet was referring too in the figure above (local link / general link: hamlet_edwin_booth.html) in a brilliant anticipation of eternal inflation. For the acorn, see the figure below (local link / general link: multiverse_acorn.html).
Eternal Inflation Further Explicated:
See the cartoon of the eternal inflation multiverse in the figure below (local link / general link: inflation_eternal.html).
The general picture of
eternal inflation is that the false-vacuum universe is infinite and eternal and sprouts infinitely many pocket universes. The false-vacuum universe plus the pocket universes is the multiverse. This picture is pictured in the cartoon of the multiverse in the figure below (local link / general link: multiverse.html).
However, the low-energy physics in other domains could be quite different from ours. The setting of the low-energy physics may be random.
The high-energy physics is assumed to be general. Also general relativity and 2nd law of thermodynamics are taken to be general. Without these concepts, we would have little guidance for understanding the multiverse.
Most other pocket universes may, in fact, be rather dull: no stars or galaxies may form or atoms may be unable to form or the domain may collapse to the quantum gravity equivalent of a black hole singularity (SC-23).
Some of the coincidences of our pocket universe may be explicable by invoking the anthropic principle. But anthropic principle arguments are often hard to make absolutely convincing although they often seem plausible (see IAL 0: A Philosophical and Historical Introduction to Astronomy: The Anthropic Principle).
Philosophically, eternal inflation is satisfying to many people: infinite and eternal and on a super-large scale homogeneous, isotropic, and unchanging with time.
But, of course, eternal inflation is only one of many inflation theories: they may none of them be right.
Is the Multiverse Subject to Falsification?
Philosopher of science Karl Popper (1902--1994) posited as a scientific principle that a scientific theory should be subject to falsification: there should be tests that if the theory fails it is falsified: i.e., wrong, NOT true.
The idea of falsification goes back at least to Blaise Pascal (1623--1622):
The status of falsification has been much debated and actually applying it is full of all kinds of contigencies, but most modern scientists accept it as a valid scientific principle, maybe with qualifications.
Now some argue that the multiverse CANNOT be falsified.
But, in fact, the multiverse keeps passing one significant falsification test as point out by Martin Rees (1942--) (in an article I CANNOT now locate) and probably others. We have already discussed the falsification test above in our discussion of eternal inflation in the cartoon of the eternal inflation in the figure above (local link / general link: inflation_eternal.html).
But to recapitulate the discussion of the falsification test:
1. The observable universe seems somewhat fine-tuned for life as we know it.
  This has be debated too, but majority view is willing to concede it yours truly thinks.
  See: Shannon Hall, 2015, SciAm, "Thank Your Lucky Constants" , Tim Maudlin, 2013, Aeon, "The calibrated cosmos", S. Borsanyi et al., 2015, Science, "Ab initio calculation of the neutron-proton mass difference", Luke A. Barnes, Geraint F. Lewis, 2017, ArXiv, "Producing the Deuteron in Stars: Anthropic Limits on Fundamental Constants", Luke A. Barnes, 2011, ArXiv, "The Fine-Tuning of the Universe for Intelligent Life".
2. One argument for the multiverse has been that this fine-tuning is evidence for it. If the observable universe could be anything, why is it just this way?
  Answer: Because we're the lucky winners.
  This is a plausible argument, but is the multiverse falsifiable? Yes.
3. Following Rees: The observable universe is NOT over-fine-tuned: i.e., more fine-tuned than is necessary for life as we know it.
  If it were over-fine-tuned, then there would be some absolute physical logic/necessity that dictates the observable universe to which life as we know it is an irrelevant accident.
4. For example, S. Borsanyi et al., 2015 calculate ab initio from theory that the neutron-proton mass difference is ∼ 0.14 % in agreement with observation (0.0013784 ????). They argue---without, alas, being very precise---that a significantly different value would have made the observable universe a lot less biophilic for consequences of Big Bang nucleosynthesis.
  But what if the mass difference were exactly 1/700 = 0.001428571 ... ≅ 0.00143? This is more fine-tuned than is needed for a biophilic observable universe.
  There must be some absolute physical logic/necessity that dictates that the neutron-proton mass ratio be exactly 701/700.
  But so if we ever experimentally verified that neutron-proton mass ratio 701/700 to sufficiently many significant figures what we were convinced that it was exactly 701/700 that would falsify the multiverse.
  Absolute physical logic/necessity would have to be really weird if 701/700 were required.
  Folks would really be scratching their heads.
  By the way, the ratio is NOT 701/700 to within uncertainty.
5. So far the multiverse keeps passing over-fine-tuning falsification tests.
  So if you require falsifiability for a scientific theory, the multiverse does have it and so far it is NOT falsified.
  Actually, it's passed all the simple ratio ones already I think. Well maybe it failed 3 spatial dimensions!!!! But if string theory is right, maybe it passed that one too.
But could we ever come to believe the multiverse is true aside from absolute philosophical skepticism?
Maybe NOT. Maybe our view of the universe is too superficial to reach that point.
Our occasional UNLV colleague Mario Livio as weighed in: see Livio, M. 2013, How Can We Tell If a Multiverse Exists?
The Status of Inflation:
How well supported is the idea of inflation?
1. It provides possible solutions for the three problems discussed above.
  It remarkably predicted Omega equal to 1 to within 1 in 10**5 (CL-155) long before observations gave Omega=1.0005(40) (Planck 2018 results. I. Overview and the cosmological legacy of Planck 2018).
2. Physicists find it plausible in terms of modern theories of particle physics (virtually synonymous with quantum field theory).
  In fact, the belief is that particle physics and cosmology are essential to each other, NOT just mutually illuminating: you have to understand both to understand the one.
3. For what it is worth, some versions of inflation like eternal inflation are philosophically satisfying to many.
4. Eternal inflation and other multiverse theories pass the NOT-over-fined-tuned falsification test.
The upshot is that the inflation paradigm has some strength and has increased in strength with time: it hasn't simply gone away as some hot concepts do.
But on the other hand, the non-uniqueness problem of inflation makes me wonder if it is the geocentric model epicycle theory of our time.
Ekpyrotic Universe:
But we still don't know the true physics of inflation. All particle physicists can give us is ideas that are plausible to them.
And there is a rival theory of the larger universe: the ekpyrotic universe (a modern version of the cyclic universe) which does as well as inflation according to its proponents (FK-676). It is based on string theory.
We will NOT discuss the ekpyrotic universe further here---the instructor hopes it will just go away. Maybe string theory will go away too.
However, inflation and the ekpyrotic universe do make different predictions about the redshifts of distant galaxies and the polarization of the CMB.
So which idea is favored may emerge soon.

Conclusion

Modern cosmology has seen many changes in observations and theory since beginning with Albert Einstein (1879--1955) and the Einstein universe (1917) in 1917 (No-520; Bo-97).

One can cite a representative sample of the major innovations:

1917: The Einstein universe (1917) and the de Sitter universe (1917) (No-520--521).
1924: The definitive observational proof of the existence of other galaxies (Wikipedia: Edwin Hubble: Universe goes beyond the Milky Way galaxy; No-510).
1920s: The FE models (No-524--525).
1929: The observational discovery of the expansion of the universe and Hubble's law by Edwin Hubble (1889--1953) (see Wikipedia: Edwin Hubble: Redshift increases with distance; Wikipedia: Expansion of the universe: History).
1930s: The first observational evidenced for dark matter (Wikipedia: Dark matter: Early history; English and Spanish Translation of Zwicky's (1933) The Redshift of Extragalactic Nebulae (Die Rotverschiebung von extragalaktischen Nebeln)); Georges Lemaitre's (1894--1966) primeval atom (No-530); various cosmological models have vogues including the Lemaitre-Eddington universe (Bo-84,85,117--121,159,175,180).
1940s: Big Bang cosmology (No-531ff,559ff).
1952: The major revision of the Hubble constant (No-528).
1965: The CMB observationally discovered (No-560ff); Big Bang cosmology comes permanently into vogue; FE Λ=0 models in vogue, particularly the Einstein-de Sitter universe (1932, standard model of cosmology c.1960s--c.1990s).
1970s: Inflation cosmology (FK-661; Ov-240,242,245).
1980s: Dark matter universally accepted as the leading theory to explain large scale motions; MOND remains a counter theory.
1990s: The observational discovery of fluctuations in the CMB (FK-640,644).
1998: The discovery of the acceleration of the expansion of the universe (FK-649); the Λ-CDM model becomes established as the standard model of cosmology (SMC).
2000s: Detailed CMB maps and the further elucidation of the Λ-CDM model.
2020s: Hubble tension and other tensions which may require a revision of the Λ-CDM model or its replacement by a new standard model of cosmology (SMC).
The advent of the James Webb Space Telescope (JWST, 2021--2041?) and other new programs and instruments: e.g., Euclid (2023--).

Are more changes are coming?

Well, very probably yes, although Big Bang cosmology as far as it goes seems robust.

Here are some questions:

Will the formation of large-scale structure continue to firm up? Probably. Seems to be doing better all the time.
What is the dark matter? We have some hope---but by no certainty---that it might be discovered within a few years or decades.
What is the dark energy? We are still pretty clueless. But there is lots more accessible observational evidence to obtain.
Will inflation continue to provide a useful framework in which to analyze the larger universe or, if it exists, multiverse?
Will MOND become important or will it go away. It seems to be losing the battle to dark matter, but it may stage a comeback.
Will particle physics and cosmology solve all their joint problems giving us the theory of everything (TOE) and the true theory of cosmology? Who knows.
Will the tensions of the Lamda-CDM model (standard cosmological model c.1995--) circa the 2020s (see Galaxies file: big_bang_cosmology_limitations.html) lead to its revision or replacement sooner or later? Or will they evaporate?
Are we on the verge of a paradigm shift to a new standard model of cosmology (SMC)? Maybe.

Some of these questions might see rapid development; others could take a long time.

In any case, as people are fond of saying, we are in the golden age of cosmology (c.1992--).

Group Activity:

Form groups of 2 or 3---NOT more---and tackle Homework 30 problems 15--20 on cosmology, the Λ-CDM model Big Bang cosmology, and inflation cosmology.

Discuss each problem and come to a group answer.

Let's work for 5 or so minutes.

The winners get chocolates.

See Solutions 30.

Appendix: The Steady State Universe (Not Required for the RHST)

A particularly famous version of the de Sitter universe is the steady state universe which had a vogue from the late 1940s to early 1960s when it was ruled out. We discuss the steady state universe in the figure below (local link / general link: fred_hoyle.html).

Appendix: The Multiverse Paradigm and Reality (Not Required for the RHST)

Yours truly has NEVER been able to write a coherent explication of the multiverse paradigm and all the considerations about reality that are connected to it.

So this section is just a list of points on these subjects in NO strict order that have occurred to yours truly.

Yours truly does NOT recommend reading this amateur excursion into philosophy.

UNDER RECONSTRUCTION BELOW

The Multiverse:
The multiverse is a paradigm for the universe as whole, observable and unobservable.
Note multiverse is just a special name for the universe as whole.
The multiverse is is highly speculative, but there is some evidence for it.
Eternal inflation is one version of the multiverse as well as being one version of inflation.
The eternal inflation version of the multiverse (as most people think of it, it seems) consists of a background universe consisting of some kind of fields understandable in quantum field theory and an infinity of pocket universes.
What are pocket universes?
Large regions in which particular initial conditions or even some physical laws are realized out of some infinity or quasi-infinity of possibilities allowed by quantum field theory, high energy physics, general relativity, quantum gravity, and thermodynamics.
The eternal inflation multiverse is eternal (as its name suggests), but pocket universes come and go.
The observable universe is embedded in "our pocket universe". We CANNOT see any trace of its edges wherever they are so far. We may be deep in the interior.
What separates the pocket universes?
In eternal inflation, there may be large, smoothly-varying transition regions of high-energy vacuum (called false vacuum which we discuss briefly below in the section Inflation and Inflation Cosmology).
But perhaps there are sharp boundaries.
Note that the eternal inflation multiverse is still governed by general relativity and this implies it CANNOT be static---it may be in overall expansion or constraction, but probably NOT uniformly: there may be some complex mixture expansion and constractions.
See the cartoon of the eternal inflation multiverse in the figure below (local link / general link: inflation_eternal.html).
The
physical laws of the pocket universes can vary as aforesaid, but arise out of the infinity or quasi-infinity of possibilities allowed by quantum field theory, high energy physics, and thermodynamics.
Note we have to impose some restrictions on the possibilities for physical laws or else we have no guidance for explicating the multiverse and admit we know nothing---perhaps we do know nothing.
The concepts of multiverse and pocket universe are very speculative. They may NOT exist. But they are persuasive to some.
And they have become necessary in discussing modern cosmology.
The consensus is that we usually use the term universe for the structure that includes and resembles the observable universe.
So we need other terms that for the universe of everything physical.
The terms/concepts multiverse and pocket universe fill that need.

Ω = ρ/ρ_c .

r(t)=a(t)*r_0 ,