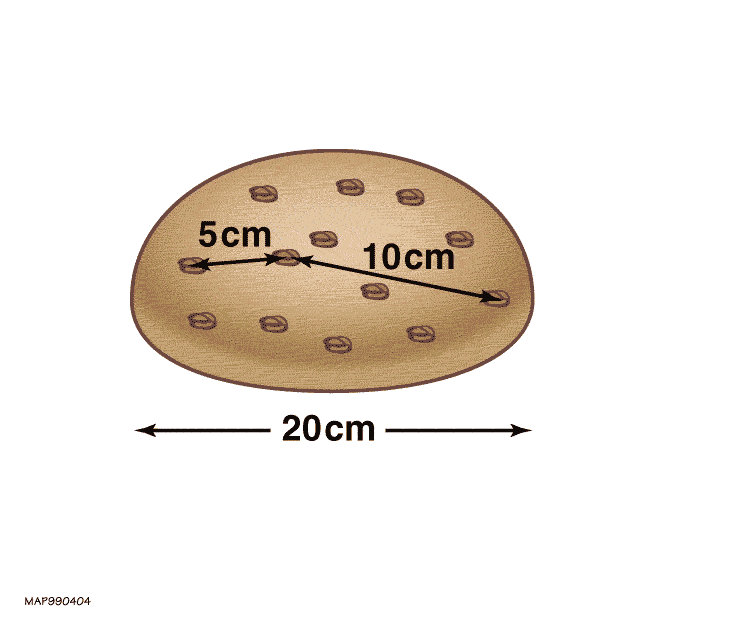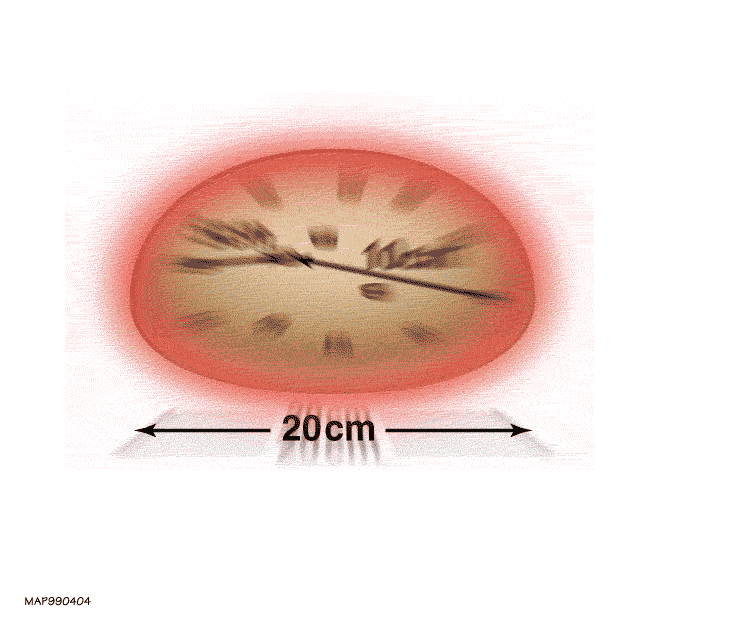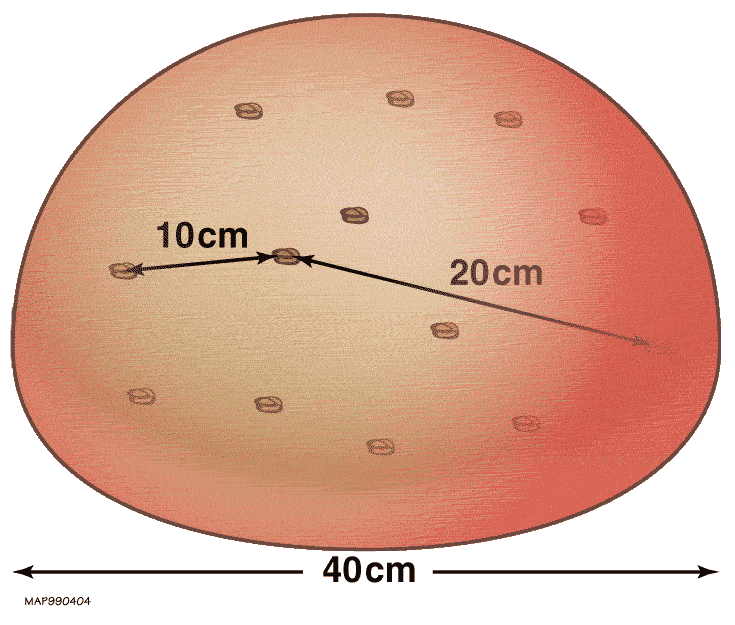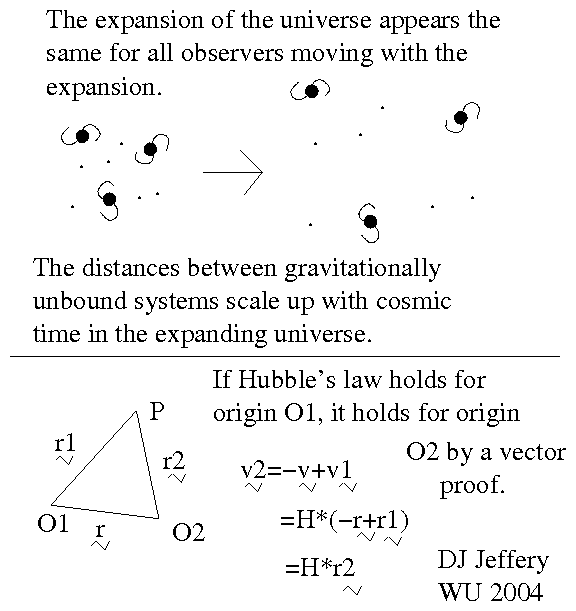
Image 1 Caption: The expansion of the universe is a literal growth of space between gravitationally unbound systems according to general relativity. All the cosmological physical distances between the gravitationally unbound systems undergo a general, uniform scaling up with cosmic time.

Gravitationally bound systems and bound systems in general do NOT expand. So you and yours truly don't expand. Moons, planets and stars don't expand. Galaxies and galaxy clusters (if they are gravitationally bound systems which they mostly are) don't expand. Galaxy superclusters, though gravitationally interacting, seem to be mostly gravitationally unbound systems, and so will probably be mostly torn apart eventually by the expansion of the universe if it continues long enough.

In Image 1, we see the ideal scaling up in cosmological physical distances between 3 spiral galaxies 6 dwarf galaxies.

The expansion of the universe is really the expansion of the observable universe. Beyond the observable universe, there is probably expansion for a long way, but we do NOT know how far it extends.

There is NO center of expansion and nothing is being expanded into as far as we can see in the observable universe. There is just a scaling up. But maybe there is a center of expansion and a realm to expand into beyond the observable universe.

Features:

1. Image 2 Caption: Inevitably the expansion of the universe is illustrated by an IDEAL loaf of raisin bread when being baked. The dough (space between bound systems) expands uniformly, but the raisins (the bound systems) do NOT expand. This illustration is de rigueur.

   

2. Image 3 Caption: An animation showing schematic gravitationally bound systems in the expanding universe.

   Note the animation gives the impression that there is a center of expansion. But everyone in the observable universe can take the perspective that they are at the center of expansion. We and they actually just see the scaling up of the observable universe.

3. Note bound systems that are NOT gravitationally bound systems (like you and me) are bound by the electromagnetic force and/or the strong nuclear force.

4. As aforesaid above, expansion of the universe is a literal growth of space. according to general relativity. Space is a kind of stuff/structure that can grow or shrink. It's NOT just emptiness.

5. The points that participate in the mean expansion of the universe define fundamental free-fall frames (which are exact inertial frames and are called comoving frames) in our modern understanding of cosmology.

   The comoving frames, in fact, form a continuum of fundamental free-fall frames throughout the observable universe.

6. The velocities between points participating in the mean expansion of the universe are NOT ordinary velocities, they are velocities between inertial frames NOT with respect to inertial frames. They are called recession velocities.

   For cosmologically remote astronomical objects, recession velocities do exceed the vacuum light speed c = 2.99792458*10**8 m/s ≅ 3*10**8 m/s =3*10**5 km/s ≅ 1 ft/ns. But this is NOT a violation of special relativity since recession velocities are NOT with respect to inertial frames

7. Actually, all astronomical objects participating in the expansion of the universe have superimposed peculiar velocities which are ordinary velocities. The peculiar velocities become small relative to recession velocities as cosmological physical distance grows, but can become relatively large for small cosmological physical distances. Close galaxies can be approaching each other as happens in galaxy mergers.

   Typically peculiar velocities are relatively small for cosmological physical distances >∼ 10 Mpc and typically become relatively large and even dominating for cosmological physical distances <∼ 1 Mpc.

8. The expansion of the universe was observationally discovered Edwin Hubble (1889--1953) 1929 (see Wikipedia: Edwin Hubble: Redshift increases with distance; Wikipedia: Expansion of the universe: History).

   Actually, several observers had partially anticipated Hubble, but he observationally discovered Hubble's law which gave the expansion behavior, and thus made the expansion of the universe a definite result. Hubble's law (which holds between points participating in the mean expansion of the universe) is

   v = Hr ,

   where v is recession velocity, r is cosmological physical distance, and we have Hubble constant H = 70 (km/s)/Mpc fiducial value accurate to within ∼ 10 %.

9. Alexander Friedmann (1888--1925) and Georges Lemaitre (1894--1966) in the 1920s before 1929 had predicted the expansion for observable universe based on Friedmann equation which is derived from general relativity plus the assumptions of the cosmological principle and that the actual matter of the observable universe could be approximated by a uniform perfect fluid.

   Willem de Sitter (1872--1934) had predicted expansion of the universe in 1917 with his de Sitter universe which was based on general relativity plus the assumptions of the cosmological principle and the cosmological constant with NO matter.

   The Friedmann equation implies Hubble's law, but it seems that the first to present Hubble's law as mathematical result explicitly was Lemaitre in 1927 in a scientific article in French in the pretty obscure Annals of the Scientific Society of Brussels. No one seems to have noticed at this mathematical result in 1927 and Lemaitre did NOT draw much attention to it.

10. What the Friedmann equation actually gives is the cosmic scale factor a(t) which gives the scaling of the expanding universe as a function of cosmic time.

    All the cosmologicalphysical distances r(t) separating points participating in the expansion of the universe scale with a(t):

    r(t) = a(t)r_0 ,

    where r_0 are the cosmological physical distances at cosmic present t_0 which is age of the observable universe = 13.797(23) Gyr (Planck 2018) according to the Λ-CDM model

    Note we define a_0 = a(t_0) = 1 by convention. Thus, the cosmological physical distances at cosmic present t_0 are also referred to as the comoving distances since they are the same for all cosmic time.

    Of course, for Friedmann equation (FE) models other than the Λ-CDM model cosmic present t_0 may have other values. In fact, for those Friedmann equation (FE) models like the de Sitter universe and the Steady State Universe which are eternal in both cosmic time directions, t_0 is usually set to 0.

    

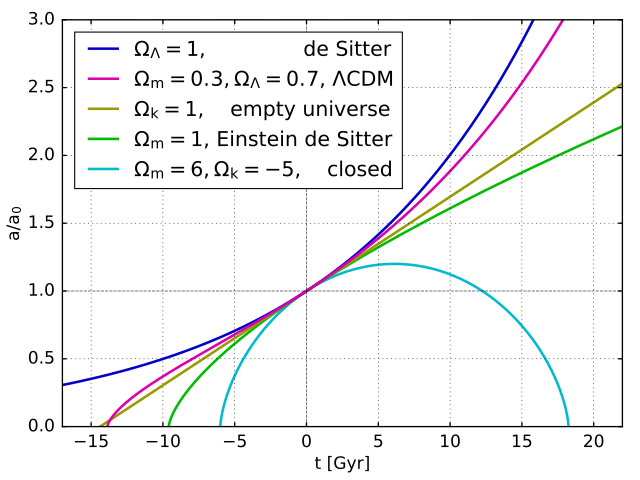
11. Image 4 Caption: The cosmic scale factor a(t) for various important Friedmann equation (FE) models:
    1. de Sitter universe (1917): blue curve. This FE model with NO mass-energy and only a cosmological constant (AKA Lambda, Λ) driver for an accelerating universe expansion of the universe. For the modern standard de Sitter universe the density parameter (AKA Omega = Ω = ρ/ρ_critical) set to Ω = Ω_Λ = 1 which gives Euclidean geometry (AKA flat space geometry). The de Sitter universe is eternal in both cosmic time directions, and so has NO Big Bang singularity.

    2. Λ-CDM model (c.1995): violet curve. This FE model has matter for its mass-energy and Ω = Ω_matter + Ω_Λ = 1 which gives Euclidean geometry (AKA flat space geometry). The Λ-CDM model and all FE models listed below have Big Bang singularities: i.e., the a(t) starts from zero at time-zero. This implies an infinite density at time-zero. In fact, we believe that the Friedmann equation and general relativity must fail as infinite density is approached and quantum gravity must take over. But there is circa 2022 NO established theory of quantum gravity, and so we are uncertain as to what happens as infinite density is approached.

       The Λ-CDM model is the standard model of cosmology (SMC, Λ-CDM model) circa 1998--2025?.

    3. Empty universe: olive curve. This is a constantly expanding, negative curvature (i.e., hyperbolic space) FE model with zero mass-energy and cosmological constant.

    4. Einstein-de Sitter universe (1932): green curve. It is flat geometry with matter as the only mass-energy, FE model with Ω_matter = 1, and zero cosmological constant.

       The Einstein-de Sitter universe (which is neither the Einstein universe (1917) nor the de Sitter universe) was probably the most standard model of cosmology (SMC) for circa 1965--circa 1998).

    5. Positive-curvature universe: aqua curve. Its only mass-energy is matter. Because of its positive curvature, this FE model has a Big Crunch singularity (i.e., an infinite density) at time-end. Just as with the Big Bang singularity, the Friedmann equation fails for a Big Crunch singularity and we CANNOT extrapolate the evolution via the Friedmann equation through the Big Crunch singularity.

       The positive-curvature universe is formally a closed universe: i.e., finite, but unbounded. It is a hyperspherical space: i.e., the curved 3-sphere space which is the surface of a 4-dimensional Euclidean geometry (AKA flat geometry) sphere. In fact, it is NOT clear that FE models can be extrapolated endlessly beyond the observable universe. If the observable universe is embedded in a pocket universe of a eternal inflation universe, then the FE models CANNOT be extrapolated endlessly beyond the observable universe. There must be point at which the behavior of the pocket universe changes in a way we do NOT know.

12. Now there may be a center of expansion and something being expanded into, but we do NOT know. As aforesaid, we just see the scaling up of the observable universe.

13. Speculative theories like eternal inflation do speculate about that the observable universe is deeply embedded in a pocket universe expanding into a false vacuum universe.

Images:

1. Credit/Permission: © David Jeffery, 2004 / Own work.
   Image link: Itself.
   
2. Credit/Permission: NASA before or circa 2007 (uploaded to Wikipedia by User:BetacommandBot, 2007) / Public domain.
   Image link: Wikipedia: File:Raisinbread.gif.
   
3. Credit/Permission: © User:Greek3 2013 CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:Cosmos-animation Empty.gif.
   
4. Credit/Permission: © User:Greek3, 2017 / CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Mplwp universe scale evolution.svg.
   

Local file: local link: expanding_universe.html.
File: Cosmology file: expanding_universe.html.