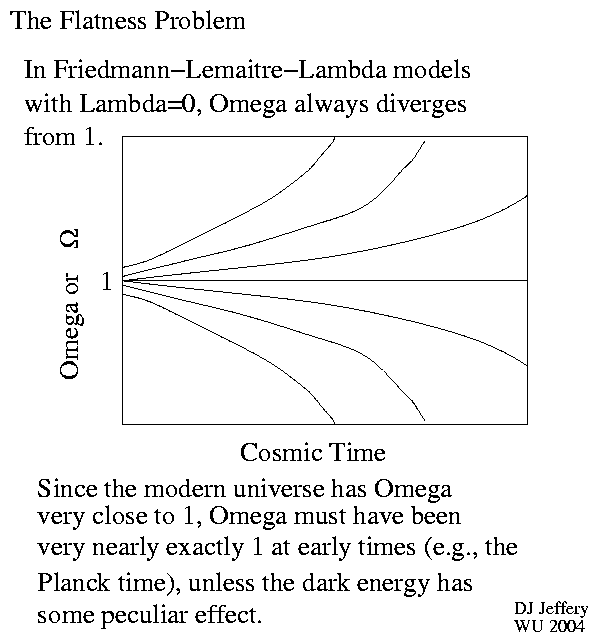
Caption: A cartoon of the divergence of density parameter Ω(t) from 1 for FE models with cosmological constant (AKA Lambda, Λ) set to zero: i.e., Friedmann-equation Λ=0 models.

Note density parameter Ω(t) = 1 gives a flat universe: i.e., a universe where space has Euclidean geometry (AKA flat space geometry).

The cartoon illustrates the flatness problem which we explicate below.

Features:

1. As a function of cosmic time, Ω(t) always diverges from 1, unless it is exactly 1 in Friedmann-equation Λ=0 models. In other words, Omega = 1 is an unstable state for the Friedmann-equation Λ=0 models.

2. If one adds a cosmological constant Λ (which is the simplest dark energy), that will eventually cause Ω(t) to converge to 1. However, for the observable universe up to cosmic time t = 10 Gyr when the observable universe transitioned from being "matter" dominated to being dominated by the cosmological constant Λ (Cahill 2017, p. 9), the cosmological constant Λ was relatively unimportant. So any significant curvature in the early universe (cosmic time (10**(-12) s -- 377700(3200) y), would have caused strong divergence of Ω(t) from 1 which would still be apparent at cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018)---but there is NO observed deviation within error from 1.

3. An analysis from the Friedmann equation models gives

     |Ω - 1| = ∝ t**(2/3) 

   where t is cosmic time for the growth of the divergence for the "matter" dominated era using of solution of the Einstein-de Sitter universe (1932, standard model of cosmology c.1960s--c.1990s) as an approximation (Li-102). We then find

    |Ω - 1|_("matter" dominated era begins = 50 Kyr)
          ≅ (50 kyr/10 Gyr)**(2/3) |Ω - 1|_("matter" dominated era ends = 10 Gyr) 
          ≅ (150*10**10 s/30*10**16 s)**(2/3) |Ω - 1|_("matter" dominated era ends)
          ≅ 3*10**(-4) |Ω - 1|_("matter" dominated era ends)  . 

   Now |Ω - 1|_("matter" dominated era ends) ⪅ 5*10**(-4) where the last value is estimated from the probably best cosmic present value |Omega-1| = 0.0005(40) (which is consistent with zero within 1 standard deviation (1 σ)) (Planck 2018 results. I. Overview and the cosmological legacy of Planck 2018, p. 31). The upshot is that |Ω - 1|_("matter" dominated era begins) ⪅ 1.5*10**(-7) which is a very tiny value.

   At early cosmic times, |Ω - 1| was even tinier. If one runs the Friedmann-equation Λ=0 models back to the Planck time t_plank = sqrt(ħG/c**5) = 5.39125*10**(-44) s, one finds

     |Ω - 1| ≅ 10**(-60) 

   (CL-155).

4. The tininess of |Ω - 1| for early cosmic time is the essence of the flatness problem.

   How could the observable universe be so flat back then? The flatness seems to be fine-tuned.

   One solution is that the observable universe was exactly flat as an initial condition.

   But then why that initial condition?

5. The inflation paradigm solves the flatness problem by positing inflation super rapid exponential expansion (much faster than in the Friedmann-equation Λ models) that flattens space.

   The inflation super rapid exponential expansion causes any curvature term in the Friedmann equation to be reduced to extreme tininess.

   In fact, the inflation paradigm predicts |Ω - 1| ⪅ 10**(-5) which is consistent with the current value |Omega-1| = 0.0005(40). (CL-155).

   This prediction for Omega was made back in the early 1980s when the observed Omega was only ∼ 0.3. Only since circa 2000 has the observed Omega come close to 1.

   It is impressive that inflation predicted the modern result before it was observed.

   It will be interesting to see if the error of the observed Omega can be further reduced and then if the agreement with inflation will still persist.

   But improving on the current Omega value with it 0.4 % error will be very difficult.

6. For an explication of inflation paradigm, see Cosmology file: inflation_paradigm.html.