Image 1 Caption: "Willem de Sitter (1872--1934), Dutch astronomer." (Slightly edited.)

Features:

1. De Sitter, who was a colleague and sometimes friendly disputant with Albert Einstein (1879--1955), presented the de Sitter universe---as we call it---in 1917 just after the Einstein universe and in the same year.

   The de Sitter universe is a general relativity cosmological model that assumes the cosmological principle and cosmological constant.

2. Remarkably both Einstein and De Sitter failed to discover the Friedmann equation which was discovered by Alexander Friedmann (1888--1925) in 1922 and independently by Georges Lemaitre (1894--1966) by 1927 (see Wikipedia: Georges Lemaitre: Career; Wikipedia: Georges Lemaitre: Work).

   The Friedmann equation is dervied from general relativity assuming cosmological principle and the perfect fluid for the mass-energy contents of the universe and allows many cosmological models (including the Einstein universe and the de Sitter universe) do be easily derived.

   Einstein and De Sitter had to use klutzier means to derive their cosmological models more directly from the Einstein field equations. Their cosmological models were pioneering works.

   

3. The de Sitter universe was the first expanding universe model. But it has with NO mass-energy, and thus zero density for the perfect fluid. It just has a cosmological constant tuned to give exponential expansion for space. Recall space has a structure according to general relativity: e.g., Euclidean space and many kinds of non-Euclidean space (i.e., curved space).

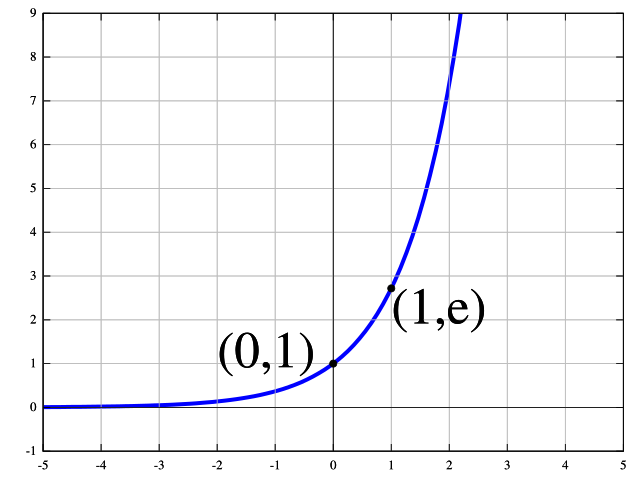
4. Exponential expansion is expansion obeying an exponential function as illustrated in Image 2 below.

5. Image 2 Caption: "The exponential function exp(x) (i.e., (e = 2.71828 ... raised to the power x), on the interval -5 to 5. The grid unit is 1 along both axes." (Somewhat edited.)

   Note despite appearances in Image 2, the exponential function only goes asymptotically to zero as the x coordinate goes to negative infinity: i.e., as x → -∞, one has exp(x) → 0.

   

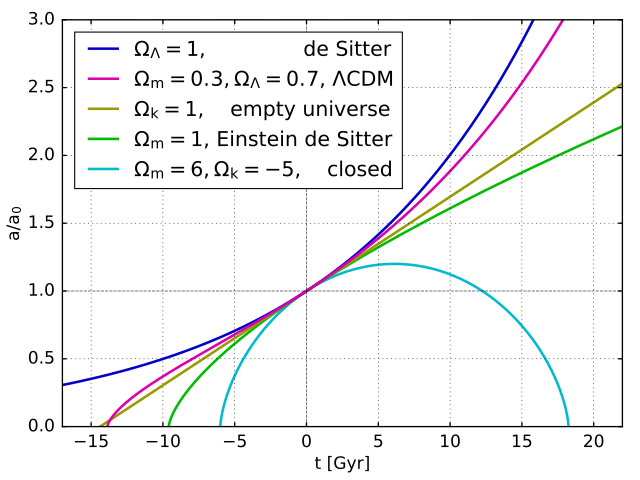
6. Image 3 Caption: See the blue curve for the cosmic scale factor a(t) for the de Sitter universe (1917).

   The formula for this cosmic scale factor a(t) is

   a(t) = a_0 exp(t/t_H) ,

   where exp(x) is exponential function, t is cosmic time measured from t = -∞ (i.e., the de Sitter universe has NO Big Bang and is eternal in both directions of cosmic time), a_0 is some fiducial scale distance (usually set to 1 for the present epoch), and t_H is the Hubble time for the de Sitter universe.

7. The original de Sitter universe had the same geometry as the Einstein universe. Thus, the original de Sitter universe is a 3-dimensional surface of a 4-dimensional hypersphere: i.e., it is finite, but unbounded, hyperspherical space (Bo-98; No-520; CL-28--29,159; O'Raifeartaigh 2019, p. 16). In modern times, we generally think of the de Sitter universe as being infinite with Euclidean geometry (i.e. flat geometry).

8. The de Sitter universe had a vogue for 15 years or so after 1917 since it had universal expansion which was observationally discovered by Edwin Hubble (1889--1953) in 1929 and had been partially anticipated earlier in the 1920s by others (most importantly by Georges Lemaitre (1894--1966) in 1927: see Hubble 1929, No-523--524, Livio 2011, Steer 2012, Way 2013, Trimble 2012, Trimble 2013, Elizalde 2018). But since the de Sitter universe had NO mass-energy, it was assumed RULED OUT by reality as being exactly true. The need for more realistic expanding universe models was filled by models with mass-energy, some with and some without the cosmological constant.

9. However, de Sitter universe predicted the cosmological redshift (O'Raifeartaigh et al. 2017, p. 39) which made it of interest circa the 1920s when most galaxies (known to be galaxies after 1924) exhibited redshifts. The prediction of the cosmological redshift by the de Sitter universe may have encouraged Hubble in the interpretation of his data.

10. The de Sitter universe has NOT gone away. The Λ-CDM model is asymptotically evolving toward being a de Sitter universe with either a cosmological constant or some more complex form of dark energy---where we count the cosmological constant as the simplest form of dark energy even if it is NOT really an energy in order to save on words though we arn't saving on them at this moment.

    Also the inflationary era (cosmic time t = 10**(-36)--10**(-32) estimated) of inflation cosmology is a de Sitter universe phase with some form of mass-energy filling the role of a cosmological constant.

11. Note that the steady state universe, which is of historical interest, is a de Sitter universe in which the continuous creation of mass-energy fills the role of the cosmological constant.

12. Note also that NEITHER the Einstein universe (1917) NOR de Sitter universe (1917) are are the Einstein-de Sitter universe which Einstein and De Sitter presented in 1932. The Einstein-de Sitter universe was probably the favored cosmological model circa 1965--circa 1998. The Einstein-de Sitter universe is Friedmann-equation Λ=0 model: i.e., it is a Friedmann-equation (FE) model with the cosmological constant (AKA Lambda, Λ) set to zero. It can have any universe geometry: i.e., hyperbolic space (Ω < 1), Euclidean space (Ω = 1), or hyperspherical space (Ω > 1). People tended to theoretically favor Euclidean space (Ω = 1) because that was simplest universe geometry, but in fact, in those days the observations tended to favor hyperbolic space (Ω < 1). See also universe_geometry.html.

Images:

1. Credit/Permission: © User:Finemann, 2001 / Creative Commons CC BY-SA 3.0.
   Image link: Wikipedia: File:WillemDeSitter3.jpg.
   
2. Credit/Permission: © Peter John Acklam (AKA User:Pjacklam), 2007 / CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:Exp.svg.
   
3. Credit/Permission: © User:Greek3, 2017 / CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Mplwp universe scale evolution.svg.