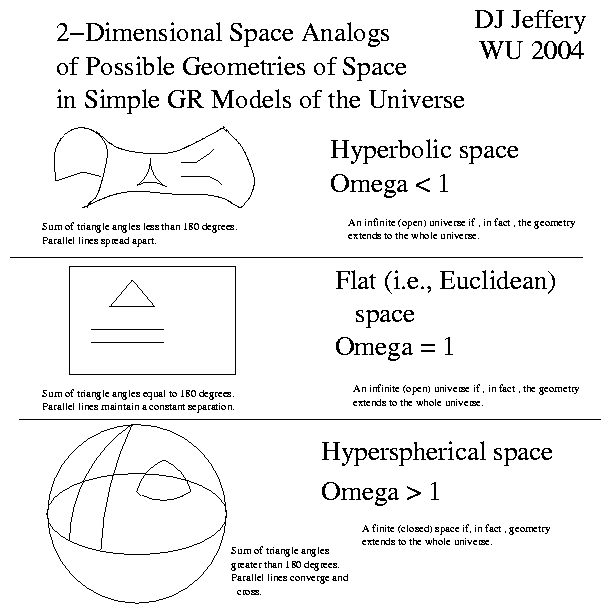
Caption: 2-dimensional space analog of possible 3-dimensional space geometries in simple GR models of the universe: i.e., the FLRW models and the FLRW-Λ models.

Features:

1. The universe geometry in the simple models is determined by the density parameter Ω which is the ratio of actual average density of mass-energy of space to the critical density of mass-energy of the models.

   Ω is a sort of dimensionless density for the universe.

2. The formula for Ω is

         Ω = ρ/ρ_c ,

   where ρ is density and ρ_c is the critical density:

   ρ_c = [3H_0**2/(8πG)]
      = (9.20387*10**(-27))*h_70**2 kg/m**3
      = (1.35983*10**11)*h_70**2 M_☉/Mpc**3    ,

   where H_0 is the Hubble constant, the gravitational constant G = 6.67408(31)*10**(-11) (MKS units), and h_70 = H/[(70 km/s)/Mpc] (see Hubble Units). Modern determinations of the Hubble constant are consistent with 70 (km/s)/Mpc to within about 5 % (see Wikipedia: Hubble's law: Observed values), and so 70 (km/s)/Mpc is a fiducial value for the Hubble constant.

3. Note that ρ, ρ_c, the Hubble constant H, and Omega are all TIME-DEPENDENT quantities.

   But Omega if greater than 1, stays greater than 1 for all time, if less than 1, stays less than 1 for all time, if exactly 1, stays exactly 1 for all time, in pure Friedmann equation models whether Λ=0 or Λ≠0.

4. Omega (i.e., Ω) decides the geometry of space and---if the models can be extended to all space---whether the universe is finite or infinite. The rule is:
   1. Omega < 1 gives a hyperbolic space (which in 2 dimensions is a saddle shape) and an infinite universe.

   2. Omega = 1 gives a flat space (i.e., a Euclidean space) and infinite universe.

   3. Omega > 1 gives a hyperspherical space (which is the 3-dimensional surface of a sphere in 4-dimensional Euclidean space) and unbounded finite universe.

   4. By the by, many people do NOT believe that the models can be extended to all space and if they are right, whether the universe is finite or infinite is NOT decided by Ω.

      These people believe the models can only be extended to our pocket universe.

   5. Remember in GR, mass-energy determines the geometry of spacetime and spacetime tells mass-energy how to move. So the universe geometry is important somehow.