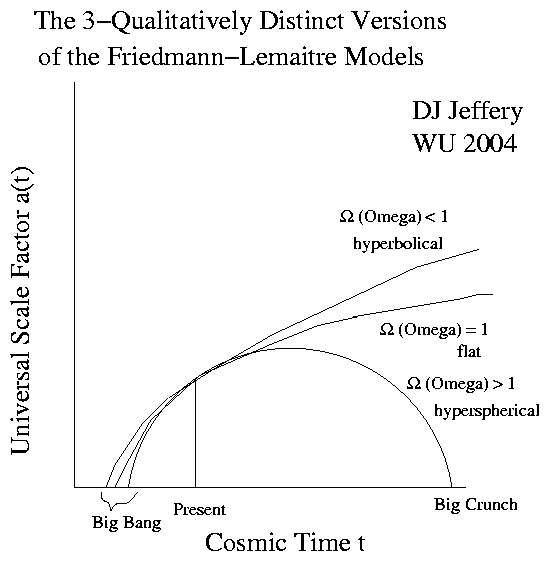
Image 1 Caption: The evolution of the cosmic scale factor a(t) in 3 qualitatively distinct versions of the Friedmann equation Λ=0 models.

Features:

1. The Friedmann equation Λ=0 models have cosmological constant (AKA Lambda, Λ) set equal to zero.

2. The density parameter Ω decides the curvature of space (i.e., the geometry of space and---if the Friedmann equation (FE) models (with Λ=0 or Λ≠0) can be extended all space (i.e., without bound)---whether the universe is finite or infinite. The rule is:
   1. Omega < 1 gives a hyperbolic space (which in 2 dimensions can be approximately represented by a saddle surface) and an infinite universe. For an explication of the hyperbolic space, see Mathematics file: space_curved.html: Image 3 Caption.

   2. Omega = 1 gives a flat space (i.e., a Euclidean space) and infinite universe. This cosmological model is Einstein-de Sitter universe (1932, SMC c.1960s--c.1990s)---note it is NEITHER the Einstein universe (1917) NOR the de Sitter universe (1917).

   3. Omega > 1 gives a hyperspherical space (which is the 3 dimensional surface of a hypersphere in 4 dimensional Euclidean space) and unbounded finite universe.

   4. By the by, many people do NOT believe that the FE models can be extended to all space, and if they are right, whether the universe is finite or infinite is NOT decided by Ω.

      Many of these many people probably believe the FE models can only be extended to our pocket universe which is embedded in the multiverse.

   5. Remember in general relativity (GR), mass-energy determines the curvature of space) and the curvature of space tells mass-energy how to move under gravity (which is a manifestation of the curvature of space). So the curvature of space is important---especially if you find yourself near a black hole event horizon.

3. The Friedmann equation Λ=0 models of the kind discussed in this figure were favored from circa 1965 (with the discovery of the cosmic microwave background (CMB): e.g., No-541,560--563) to circa 1995--1998 (e.g., Scott 2018). After circa 1995--1998, the Λ-CDM model became the standard model of cosmology (SMC) and it still is circa 2025 plus.

   

4. Image 2 Caption: Clockwise: Albert Einstein's (1879--1955), Paul Ehrenfest (1880--1934), Willem de Sitter (1872--1934), Hendrik Lorentz (1853--1928), and Sir Arthur Eddington (1882--1944) in the office of de Sitter, Leiden University, Leiden, the Netherlands, 1923.

5. In fact, the most favored Friedmann equation Λ=0 models was the Einstein-de Sitter universe (1932)---which is NEITHER the Einstein universe (1917) NOR de Sitter universe (1917).

   The Einstein-de Sitter universe is actually the simplest of all FE models: it has cosmological constant Λ=0 and density parameter Ω = 1 (i.e., it has zero curvature of space, and so has Euclidean geometry (AKA flat space geometry)).

   The formula for the cosmic scale factor a(t) of the Einstein-de Sitter universe is just

     a(t) = [(3/2)H_0*t]**(2/3) 
          = [(3/2)(t/t_H)]**(2/3) = (t/t_0)**(2/3)  , 

   where H_0 is Hubble constant, t_H is the Hubble time, and t_0=(2/3)t_H=(2/3)(1/H_0) is the age of the universe.

   Albert Einstein (1879--1955) and Willem de Sitter (1872--1934) in their 1932 article, in fact, did want to present the simplest possible FE model that could account for the then-current observations of the observable universe (see O'Raifeartaigh et al. 2015, p. 1).

   They did NOT present any theory about the POINT ORIGIN at t = 0 which we now call Big Bang singularity. The reason for their simplest model approach and lack of POINT ORIGIN discussion is that they did NOT want indulge in highly speculative theorizing at least in their 1932 article which was rather brief (see O'Raifeartaigh et al. 2015, p. 1, 6, 23).

6. The Einstein-de Sitter universe by circa 1965 became the favored FE model because it was simple and accounted for observable universe as understood then. Importantly, it had the POINT ORIGIN and therefore allowed for Big Bang cosmology which became highly favored after the discovery of the cosmic microwave background (CMB) in 1965.

   However, by 1995, the Einstein-de Sitter universe was beginning to be seen to be inadequate. At that time Ω_matter (i.e., the density parameter due to matter only: baryonic and dark) was being found to be ∼ 0.3 and NOT 1. This is still the case (see Planck 2018, p. 15). But inflation cosmology (proposed 1979) (which had become highly favored as it still is circa 2025 plus) required Ω ≅ 1. This suggested there was mass-energy that was NOT matter. So the idea of dark energy was introduced which in respect to the Friedmann equation (but NOT other respects) is equivalent to the cosmological constant Λ. Then in 1998 acceleration of the universe was discovered which could be accounted for by an nonzero cosmological constant Λ or dark energy. Very soon the Λ-CDM model became standard model of cosmology (SMC) which as aforesaid, it still is circa 2025 plus. After circa 1998, the Einstein-de Sitter universe became a subject for textbooks and history of cosmology.

7. It is historically interesting to note that the Einstein-de Sitter universe (1932) was almost the first consideration of FE models with Ω = 1 (see O'Raifeartaigh et al. 2015, p. 5). Alexander Friedmann (1888--1925) in published work only ever considered FE models with Ω > 1 (implying hyperspherical space) and Ω < 1 (implying hyperbolical space). And Georges Lemaitre (1894--1966) in published work only ever considered only FE models with Ω > 1 (implying hyperspherical space). For possible reasons for this choice of Lemaitre, see Astronomer file: georges_lemaitre.html: The Lemaitre universe (1933).

Images:

1. Credit/Permission: © David Jeffery, 2004 / Own work.
   Image link: Itself.
   
2. Credit/Permission: © H. van Batenburg, 1923 (uploaded to Wikimedia Commons by User:Vysotsky, 2014) / CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:PhysicistsinLeiden.jpg.