Flat and Curved Spaces
Explication:
- In everyday life,
we are used to thinking of
Euclidean space: i.e.,
space as exhibiting
Euclidean geometry (AKA flat geometry)
which is just the geometry we learn in high school.
In Euclidean space:
- parallel lines NEVER meet and NEVER diverge.
- the sum of the angles of a triangle add up to 180°
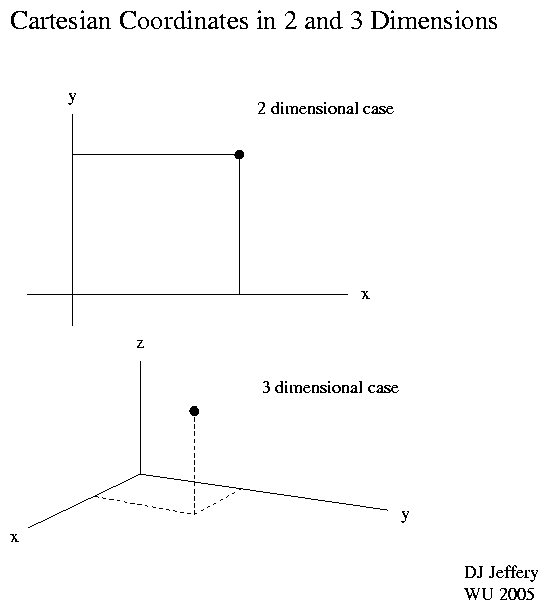
- space can be mapped in a natural way (or straightforward way) by Cartesian coordinates as in Image 1 below. Some non-Euclidean geometries can be mapped by Cartesian coordinates too, but there is NO uniquely good way to do this.
- Image 1 Caption: Cartesian coordinates in 2 and 3 dimensions.
Cartesian coordinates are good for describing Euclidean space (AKA flat space)---the space of ordinary geometry: i.e., Euclidean geometry.
- But besides Euclidean space, we are used to 2 curved spaces. They are everywhere and we are used to dealing with them intuitively (i.e., via life experience).
But we do NOT usually study them mathematically, because that is hard. Harder are 3 curved spaces because we have NO intuitive understanding.
- The study of curved spaces in general is called differential geometry or, virtually synonymously, non-Euclidean geometry. Actually, Euclidean geometry (AKA flat geometry) is considered a special case of non-Euclidean geometry.
- In fact, general relativity (1915) tells us that 3-dimensional physical space is actually curved space where the curvature varies with location in a complex way in general.
We do NOT notice the curvature, because it is so small on on our scale (except near strong gravity sources like black holes).
We are microbes living on beach ball. To us, the world is an infinite flat plane.
- However, we can get some understanding of 3 curved spaces by studying 2 curved spaces.
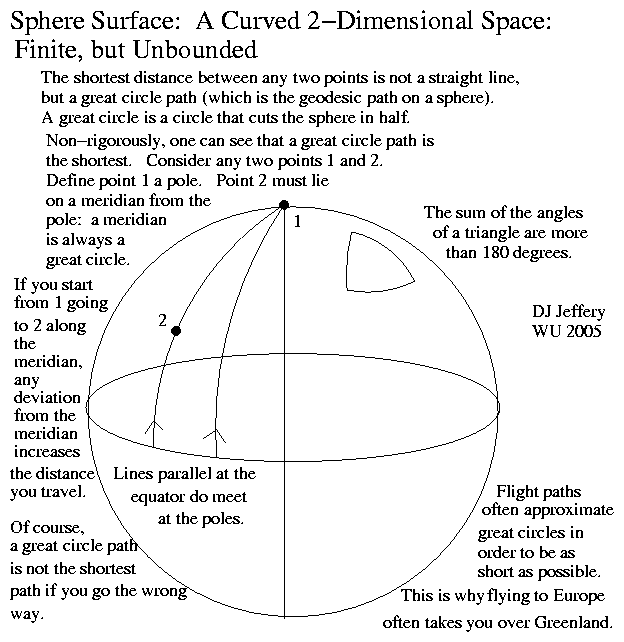
- Image 2 Caption: An illustration of the surface of a sphere which is a 2-dimensional curved space. Note it is a finite, but unbounded space: there is NO boundary. The geometry of the surface is called spherical geometry.
Features:
- An ordinary sphere
is 2-sphere
in the n-sphere classification scheme
because its surface is a 2-dimensional curved space.
- The surface of sphere
is probably the simplest
curved space to understand
by human intuition.
We will explicate
spherical geometry a bit below.
- First note that the generalization of
a straight line
to non-Euclidean geometry
is called
geodesic.
It is the
stationary path
between points
in spaces with general curvature.
A stationary path is
one where infinitesimal variations from it cause NO change in length.
Minimum
and maximum paths,
(global or local)
are stationary paths.
Stationary paths
are analyzed by
variational calculus.
- For spherical geometry,
the geodesics
are great circles which
are circles
that cut a
sphere in
half.
Circles that do NOT cut a
sphere in
half are
small circles.
Airways for aviation often follow great circles on Earth at least approximately since that shortens travel distance and travel time. This is why flights from New York City to Paris often go over Greenland.
For more on flights on great circles, see the figure below (local link / general link: great_circle_path.html). If the figure is absent, it can be seen at Mathematics file: great_circle_path.html.
- In the limit of asymptotically small regions, a 2-dimensional curved space become a 2-dimensional flat space. This is why to early societies, the Earth seemed a flat space on average.
- Now 2 geodesics are considered parallel where a third geodesic intersects them both at 90°. But in general such geodesics are only parallel for certain places.
Consider the sphere in Image 2. Note that the equator intersects two meridians both at 90°, but they are NOT parallel elsewhere and, in fact, meet at the poles.
In Euclidean geometry, of course, geodesics (i.e., straight lines) that are parallel at one place are parallel everywhere and NEVER meet. This is the same as saying that anywhere along them there is a third geodesic that intersects them both at 90° and has the same length.
- The generalization of the triangle to a general 2-dimensional space is three geodesic segments that are joined at vertices: i.e., a spherical triangle. The sum of the vertex angles (measured within the 2-dimensional space) is > 180°. Only in the limit of the spherical triangle going to zero size does it asymptotically approach being an ordinary triangle having sum of the vertex angles being 180°.
By inspection of Image 2, it is clear that the sum of the vertex angles for a triangle in spherical geometry is greater than 180°.
- In the limit of asymptotically small regions, a 2-dimensional curved space become a 2-dimensional flat space. This is why to early societies, the Earth seemed a flat space on average.

- Image 3 Caption: A saddle surface where the saddle point is the point which is maximum along one geodesic and a minimum along a perpendicular geodesic.
Features:
- Near the
saddle point,
a saddle surface
approximates a
2-dimensional
hyperbolic space
and for this reason
a saddle surface
(like the one shown in Image 3)
are used to illustrate
2-dimensional
hyperbolic spaces.
For further information,
see
Wikipedia:
Hyperbolic space: Euclidean embeddings and
Google AI question:
Does a saddle surface approximate hyperbolic space?.
- Note the
vertical direction
in Image 3 has NO
meaning for the
represented 2-dimensional
hyperbolic space.
- The representational aspect of the
saddle surface
is demonstrated by: e.g.,
- Near enough to the saddle point, a triangle constructed from 3 geodesics has a sum of the vertex angles < 180° which like a hyperbolic triangle in a real 2-dimensional hyperbolic space.
- There are approximately
ultraparallel lines:
i.e., 2
geodesics
that at their point of closest approach can be joined by
a third unique geodesic
that is perpendicular
to both of the said 2
geodesics.
- But what of a directly noticeable curved space? How would that look if we were embedded in it. It's tricky, but some idea is given by the video Spherical Geometry Is Stranger Than Hyperbolic - Hyperbolica Devlog #2 | 4:00 below in Curved space videos (see the insert below local link / general link: curved_space_videos.html).
- EOF
-
Images:
- Credit/Permission: ©
David Jeffery,
2005 / Own work.
Image link: Itself.
- Credit/Permission: ©
David Jeffery,
2005 / Own work.
Image link: Itself.
- Credit/Permission: User:LucasVB,
2007 /
Public domain.
Image link: Wikipedia: File:Hyperbolic triangle.svg.
File: Mathematics file: space_curved.html.