Newtonian Cosmology

Sections:

Introduction
Newton's Newtonian Cosmology
Newtonian Cosmology from the 18th Century the 1930s
Relativistic Cosmology (1917--)
Modern Newtonian Cosmology (1934--)
Could the Friedmann Equation Have Been Discovered Before General Relativity?

Newtonian Cosmology:

Introduction:
In this insert, we discuss Newtonian cosmology from Isaac Newton (1643--1727) to modern Newtonian cosmology (1934--).
Newton's Newtonian Cosmology:
1. Isaac Newton (1643--1727) (see the figure below: local link / general link: newton_principia.html) certainly thought in terms of an infinite or quasi-infinite (i.e., apparently infinite) universe filled with stars (No-374--377). He had matured in astronomy very far advanced beyond that of Nicolaus Copernicus (1473--1543) (see IAL 4: History of Astronomy: Isaac Newton (1643--1727)).
2. In unpublished work, Newton tried to construct a physically consistent STATIC MODEL of such an infinite universe full of stars---using Newtonian physics, of course (No-374--377).
  A physically consistent model is one with NO violations of the assumed physical laws. The boundary conditions and initial conditions of a physically consistent model may or may NOT be required to be physically real. Of course, a physically consistent model may be completely WRONG with respect to reality. The best you can usually hope for is that it approximates reality to some degree.
3. In fact, Newton's law of universal gravitation suggested to Newton that stars initially at rest in Newtonian absolute space (the singular fundamental inertial frame of the original formulation of Newtonian physics) would all collapse into a single clump centered at the center of mass in any initially STATIC FINITE model (No-375). Newton himself actually preceded the ideas of energy and conservation of energy, and so he was probably vaguely assuming any bouncing of the clumping matter making up the stars would damp out somehow. But the conclusion that there would be a collapse seemed inescapable.
  The Newtonian physics single clump endpoint is a sort of analogue to the Big Crunch of some general relativistic Friedmann equation (FE) models illustrated in the figure below (local link / general link: big_crunch.html).
4. However, what if there was an STATIC INFINITE universe with the stars uniformly spread out on average. It seemed likely to Newton that such a system could be NOT be in stable equilibrium (i.e., at rest and always returning to being at rest given any perturbation) given Newtonian physics. Any balance of gravitational forces in such universe would give an unstable mechanical equilibrium---any perturbation would start it evolving into clumps. Newton's understanding of this clumping was based on the shell theorem which he had discovered though NOT using the name shell theorem (No-375--376). From a modern understanding, the clumping might end in something like a distribution of dark matter halos sustained against further collapse by rotational kinetic energy. Newton's own thinking was maybe there was a stable equilibrium of stars if you adjusted the initial positions just right, but he was NOT satisfied with this vague hypothesis and left off his researches on Newton's Newtonian Cosmology at this point (No-375--376).
5. Note, as aforesaid, Newton left Newton's Newtonian Cosmology unpublished, and so probably felt it was all half-baked and perhaps wrong. He liked ALL-BAKED publications that were all right. Newton may NOT have been interested enough in Newton's Newtonian Cosmology to come to a good conclusion about it. He may have assumed (and some of his contemporaries did assume) that God actively intervened to save the universe collapsing into clumps (No-375).
6. In fact, the essential problem in Newtonian cosmology was how to deal with infinite quantities: e.g., infinite space and infinite mass. Pure Newtonian physics does NOT give an answer. Extra hypotheses were needed to extend Newtonian physics
7. Image 1 Caption: statues of Isaac Newton (1643--1727) and Gottfried Wilhelm von Leibniz (1646--1716), Oxford University Museum of Natural History, University of Oxford, Oxford, England. The rivals.
8. Actually, when Newton was very old in 1721, he was informed of Olbers' paradox (though NOT by that name) which seems to rule out an STATIC eternal infinite universe with the stars uniformly spread out on average (see Cosmology file: olbers_paradox.html). However, the elderly Newton does NOT to have done any further significant work on Newtonian cosmology in light of Olbers' paradox.
Newtonian Cosmology from the 18th Century the 1930s:
1. In the 18th century, Thomas Wright (1711--1786), Immanuel Kant (1724--1804) and Johann Heinrich Lambert (1728--1777) all speculated on Newtonian cosmology (see Astronomer file: immanuel_kant.html).
2. Image 2 Caption: Johann Heinrich Lambert (1728--1777): astronomer mathematician, philosopher, physicist. One of the first to theorize that some of the nebulae (historical usage) were other galaxies and to do Newtonian cosmology.
3. Wright, Kant and Lambert all theorized correctly that the Milky Way was supported against gravitational collapse by rotation around the Milky Way center of mass.
  Remarkably, this theory was NOT widely accepted by astronomers from 18th century to circa 1920s. Many astronomers believed the Milky Way was the whole universe, finite or otherwise, and was STATIC on average (IAL 26: The Discovery of Galaxies: The Discovery of Galaxies: An Example of the Process of the Scientific Method; Bo-75). However, this STATIC universe was NEVER made into a consistent Newtonian cosmology (Bo-75).
4. A logically viable compromise theory between the various ideas just discussed was an infinite empty-space universe consisting only of Newton's absolute space, except for a finite Milky Way rotating about its center of mass. But this seems physically/philosophically unsatisfying. Why an infinite universe just for the Milky Way?
5. To return to Wright, Kant and Lambert: they all thought that at least some of the nebulae (historical usage) were other galaxies. What they thought of the size and stability and motion of their respective universes of galaxies would take more research into their thinking than yours truly feels it is worthwhile to pursue. However, Kant went beyond Newtonian physics and pictured a cyclic universe (finite or NOT) where there was a cycle of conflagrations and rebirths of the universe. It seems likely that Kant for his cyclic universe was reaching far back to the Stoic physics of Greco-Roman Antiquity (c.800 BCE--c.500 CE).
6. Remarkably, nothing worth mentioning seems to have been done Newtonian cosmology until the 1930s which was after the advent of general relativity (1915) and general relativistic cosmology (more precisely the Friedmann equation models,1917--).
Relativistic Cosmology (1917--):
1. Modern cosmology on the scale of the observable universe is treated using general relativity (1915) or some extension of that.
  The begining of general relativistic cosmology was with the Einstein universe discovered in 1917 by by Albert Einstein (1879--1955). But Einstein made the discovery the hard way WITHOUT the Friedmann equation (1922) which we discuss below.
2. However, below the scale of the observable universe, is the large scale structure and that is almost always treated using using Newtonian physics for gravity and large motions of matter.
3. Why? Newtonian physics gives almost the same answers as general relativity and is much less computationally demanding. The use of Newtonian physics is NOT the limiting error in structure formation computer simulations. Other physical inputs and numerical methods are the limiting errors. Of course, general relativistic structure formation computer simulations have been done to prove the that use of Newtonian physics is NOT the limiting error.
4. The upshot is that there is still a vast realm for Newtonian physics in modern cosmology.
5. What of on the scale of the observable universe and beyond that? General relativistic cosmology is needed.
  The key component of general relativistic cosmology is the Friedmann equation (1922) discovered by Alexander Friedmann (1888--1925) and independently by Georges Lemaitre (1894--1966) circa 1927.
6. Image 3 Caption: Alexander Friedmann (1888--1925) serving as an aviator in Imperial Russian Air Service, Imperial Russian Army, World War I (1914--1918), 1916 Aug01. A Russian-Soviet aviator, ballonist, mathematician, meteorologist, physicist, pioneering cosmologist, and discoverer of the eponymous Friedmann equation in 1922. See also Astronomer file: alexander_friedmann.html , Wikipedia: Alexander Friedmann, The MacTutor History of Mathematics archive: Aleksandr Aleksandrovich Friedmann.
7. For most research in modern cosmology, all that is needed from general relativity is the Friedmann equation (see Astronomer file: alexander_friedmann.html ).
8. The fundamentally correct derivation of the Friedmann equation is from general relativity plus the assumptions of the cosmological principle and the perfect fluid (see IAL 30: Cosmology: Einstein, General Relativity, and the Einstein Universe: Einstein's Simplifying Assumptions for the Einstein Universe).
9. The solution of Friedmann equation is the cosmic scale factor a(t) which gives the scaling up of the observable universe as a function of cosmic time t.
10. Of course, there are many solutions of the Friedmann equation. Exact analytic solutions give the behavior for relatively simple evolutions of a(t) and numerical solutions are needed otherwise. In fact, the Lambda-CDM model well after the radiation-matter equality time (t=51.7(8) kyr) (i.e., well after the (radiation era (inflation end 10**(-32) s ? -- 51.7(8) kyr)) is governed by an exact analytic solution (e.g., Jeffery 2026, p. 25???).
11. The Friedmann equation models all naturally predict the expansion of the universe or the contraction of the universe. A static universe only occurs for a fine-tuned cosmological constant (AKA Lambda, Λ). In fact, the Einstein universe (1917) is a static universe model (see IAL 30: Cosmology: Einstein, General Relativity, and the Einstein Universe).
12. Actually, the theoretical Hubble's law is a direct consequence of the Friedmann equation. Alexander Friedmann (1888--1925) must have known this, but did NOT explicitly show it in his published works. Georges Lemaitre (1894--1966) is justly credited with the explicit discovery of the theoretical Hubble's law in 1927 (see Astronomer file: georges_lemaitre_cartoon.html ).
13. So both the expansion of the universe and Hubble's law were theoretical predictions of Friedmann equation before their observational discovery by Edwin Hubble (1889--1953).
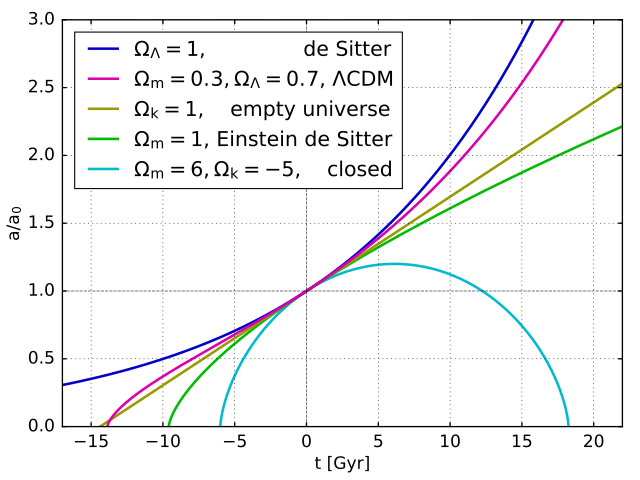
14. Image 4 Caption: Examples of interesting cosmic scale factor solutions a(t): the de Sitter universe (1917), the Λ-CDM model (the standard model of cosmology (SMC) since circa 1995: e.g., Scott 2018, p. 10), Einstein-de Sitter universe (1932) (which is NEITHER the Einstein universe (1917) NOR the de Sitter universe (1917)), a linear growth solution (e.g., the empty universe or Rh=ct universe (2011)), and the positive curvature universe (AKA closed universe).
Modern Newtonian Cosmology (1934--):
1. In fact, with reasonable extra hypotheses, the Friedmann equation (and the 2nd Friedmann equation too) can be derived from Newtonian physics plus the assumptions of the cosmological principle and the perfect fluid also used in the derivation from general relativity.
  We will NOT give NOR explicate this derivation.
  But there is a KEY FACT to note, the extra hypotheses do NOT yield a general theory from which Newtonian physics emerges in the classical limit. The extra hypotheses just imply there is such a general theory. The general theory is, in fact, general relativity.
  Thus, although you account for the overall evolution of the observable universe (via the Friedmann equation) and large-scale structure of the universe (which can be done to high accuracy/precision with Newtonian physics) in Newtonian cosmology, Newtonian cosmology (since it does NOT rely on a fully consistent physical theory which is general relativity) will always be judged unsatisfactory.
  The upshot is that for the hope of a satisfactory cosmology, we need to have that cosmology rely on general relativity or whatever improved theory of gravity that might replace it.
2. However, the Newtonian physics derivation of the Friedmann equation is extremely useful in understanding the Friedmann equation and in teaching it in cosmology courses, where, in fact, general relativity is mostly skirted since one CANNOT do everything.
3. Remarkably, the Newtonian physics derivation of the Friedmann equation was first done in 1934 by William McCrea (1904--1999) and E.A. Milne (1896--1950) which was 12 years after Alexander Friedmann (1888--1925) first derived it in 1922 from general relativity (Wikipedia: Friedmann equations; Wikipedia: Friedmann-Lemaitre-Robertson-Walker metric: Newtonian interpretation).
Could the Friedmann Equation Have Been Discovered Before General Relativity?:
1. Yes. The Friedmann equation could have been derived as early as the 18th century.
2. Johann Heinrich Lambert (1728--1777) could have done it if he had just followed the NOT-very-hard right mental path. However, he could NOT have understood that the integration constant that turns up in the derivation determines the curvature of space since understanding this integration constant needs general relativity. He would have thought of Euclidean space (i.e., flat space) universe.
3. Also, it was probably beyond Lambert's physical intuition to hypothesize that the Friedmann equation does allow for the non-conservation of mass. The hypothesis can just be introduced as wild speculation, but more physically motivated path to it uses thermodynamics, E=mc**2, and general relativity (or at least an extra hypothesis instead of), none of which were available to Lambert.
4. Actually, the chief problem 18th century and 19th century astronomers had in a derivation of Friedmann equation in Newtonian cosmology was probably that they had to replace the assumption of Newtonian absolute space (the singular fundamental inertial frame) by the assumption that all free-fall frames unrotating with respect to the observable universe constitute an infinite set of fundamental inertial frames (see Mechanics file: frame_basics.html ).
  In practice, when doing celestial mechanics those 18th century and 19th century astronomers effectively made this replacement all the time. But they did NOT make the mental leap that it should be done in principle. The mental leap was done by Albert Einstein (1879--1955) in deriving general relativity (1915).

Images:

Credit/Permission: Anonymous artist circa 1770 (uploaded to Wikimedia Commons Wikipedia by User:Mahlum, 2005) / Public domain.
Image link: Wikimedia Commons: File:JHLambert.jpg.
Local file: local link: .html.
Credit/Permission: © User:Andrew Gray, User: Alexey Gomankov, 2016 / Creative Commons CC BY-SA 3.0.
Image link: Wikimedia Commons: File:Statues of Isaac Newton and Gottfried Leibniz.jpg.
Credit/Permission: Anonymous photographer 1916 (uploaded to Wikimedia Commons Wikipedia by User:Ctac, 2015) / Public domain.
Image link: Wikimedia Commons: File:Fridman AA.jpg.
Credit/Permission: © User:Greek3, 2017 / CC BY-SA 4.0.
Image link: Wikimedia Commons: File:Mplwp universe scale evolution.svg.

local link: newtonian_cosmology.html

Cosmology file

newtonian_cosmology.html