In this insert, we introduce the basics of reference frames relevant to physics.
In particular, we cover inertial frames which are overwhelmingly the MOST relevant reference frames for physics.
Inertial frames are NOT hard to understand: in fact, they are reference frames you use and think about all the time in everyday life and use for Newtonian physics applied to everyday life situations.
But if you want to cover every finicky detail---as yours truly is doomed to do---then the explication goes on and on.
Correctness and clarity are possible, brevity NOT.
What are reference frames?
Just a set of coordinates
you lay down on
geometrical space
(e.g., the
(3-dimensional physical) space
which includes the
3-dimensional space
of outer space)
or, including time,
on spacetime
as we say in relativity speak.
See the figure below
(local link /
general link: frame_reference_spacetime.html)
for an example reference frame
which includes time
coordinates.
The key feature of
inertial frames is that
all physical laws in the
observable universe
are referenced to
inertial frames,
except
general relativity
which tells us what
inertial frames are.
You can quibble about whether there are
other physical laws
NOT referenced to
inertial frames, but
yours truly thinks the quibbling is a matter of perspective
or may amount
to saying you are NOT using
inertial frames in some
definitional sense when effectively you are using them.
Fortunately, except in calculations needing
general relativity,
you can always find an
inertial frame
to do your calculation in.
In fact, you can find an infinity of
inertial frames,
and so can choose one that is convenient for your calculation and understanding.
Note:
You do NOT need to find them.
Their properties emerge from
general relativity
where they are needed.
However, full
general relativity
calculations
are usually very computationally expensive and in many cases intractable.
So you do NOT use
general relativity,
except when you need to.
And if you are NOT using
general relativity,
you need to find
inertial frames
to do your calculations in.
The observable universe
as a whole CANNOT be mapped to a
single inertial frame.
In fact, treating the
observable universe
as whole requires
general relativity.
However---and there is always a however---Newtonian physics
with the definition of
inertial frames
given by
general relativity
(see the below sections
Ideal Inertial Frames
and
Center-of-Mass (CM) Inertial Frames)
can describe the
observable universe
as whole to good
approximation.
Isaac Newton (1643--1727)
actually posited a
theory
of a singular fundamental
inertial frame, but
the advent general relativity
required that
theory to be discarded.
For more on
Newton's absolute space,
see the below section
Newton's Absolute Space
(Not Required for the RHST).
Instructor: Just cover item 1 and explicate the others in brief with the cartoons below.
Instructor: Just cover the first three items and explicate the others in brief with the cartoons below.
You can then analyze the
motions of the system
relative to the
center of mass
(i.e., INTERNAL motions)
using both INTERNAL forces
(i.e., those generated inside
system)
and EXTERNAL
forces
(i.e., those generated outside
system).
It is usually best to choose the
systems for analysis
in such away that
the EXTERNAL
forces
are as small as possible.
If the system
of objects
is NOT in
acceleration relative the
EXTERNAL inertial frame,
it is already an
inertial frame.
If it is in acceleration,
you impose
inertial forces
to convert it to an
inertial frame.
You can always choose a different
reference frame
(often a larger reference frame)
that is an inertial frame
or
convert the
non-inertial frame
into an inertial frame
using inertial forces
and this done all the time when convenient (i.e., usually when the
acceleration is smooth enough).
The conversion to an
inertial frame
is explicated in the figure below
(local link /
general link: frame_rocket_room.html).
Actually, a qualification is needed from
general relativity
about
inertial frames
and rotation relative to the
observable universe.
There may be
reference frames
that are inertial frames
(in a sense)
rotating relative to the
observable universe
in very strong gravitational fields
such as near black holes.
But yours truly CANNOT find any reference that elucidates this
qualification.
It is hinted at by
Wikipedia:
Inertial frame of reference: General relativity.
Yours truly will usually NOT refer to the qualification again.
Note, the qualification is required by
general relativity
and is NOT present in
Newtonian physics as
inertial frames are now understood in
Newtonian physics.
Since the mid 1990s,
it has been known that the
expansion of the universe is an
accelerating expansion of the universe.
The fundamental explanation of the
accelerating universe is
NOT known.
However, the
cosmological constant
(given symbol
capital Greek Lambda = Λ,
and so often referred to as
Lambda or
Λ)
is the simplest explanation and one
that gives the
right behavior for
accelerating universe
and
structure formation (AKA large-scale structure formation)
to good approximation.
In general relativity,
the cosmological constant
just adds a term to
Einstein field equations,
and so is, in fact, a feature of
gravitation.
In a Newtonian physics sense,
the
cosmological constant effect
acts like as pushing
force
on matter
that grows linearly with distance from
any point which means it grows to infinity as you go to infinite distance.
However, the infinity aspect is NOT a concern for calculations
interior to a finite
system treated
with an inertial frame.
In such
systems, the
cosmological constant effect
(i.e., the
cosmological constant force)
just pushes outward from the
center of mass
on all
particles
and/or objects
In fact, the
cosmological constant force
is probably completely negligible for
systems
smaller than galaxies
and probably small even for
galaxies and
galaxy clusters.
Its importance mainly for the
comoving frames
and the observable universe
as whole.
One often hears that
accelerating expansion of the universe
is caused by
dark energy.
In fact,
the cosmological constant
and
dark energy
(i.e., constant dark energy)
are often conflated because they have the
same effect in astrophysical and cosmological
contexts.
So when someone says
the cosmological constant
or dark energy, they can mean
either one or the other or both.
Context decides
what they mean.
For simplicity in discussions, yours truly
just considers the
cosmological constant
the simplest form
of dark energy even though
it is NOT actually a form of
energy at all, but
an aspect of
gravitation as aforesaid.
The constant
dark energy
is the second simplest form of
dark energy (in
yours truly's discussions).
As aforementioned, dark energy
acts just like
the cosmological constant
in astrophysical and cosmological
contexts, but
has different properties in other
contexts.
There are more complicated theories
of dark energy
called
dynamical dark energy theories.
At present, we do NOT know which if any known
theory
of dark energy
(including the cosmological constant)
is right.
Dark energy is really a
word for our ignorance.
We see an effect
(i.e., accelerating expansion of the universe)
and we attribute it to a cause whose properties other than effect we do NOT know.
How inertial frames
turn up on the
Earth
in everyday life
is explicated in the
figure below
(local link /
general link: frame_inertial_free_fall.html).
Note, the discussion in the figure generalizes,
mutatis mutandis,
to almost all compact astro-bodies
(i.e., those NOT held up by kinetic energy,
except neutron stars
and black holes which
require relativistic physics)
since they are almost all subject to
tidal forces and,
since they are almost all in
rotation relative to the
observable universe, have
the rotating frame
inertial forces: i.e.,
the centrifugal force,
Coriolis force,
and Euler force.
We are merely using the
Earth as an important-to-us
concrete example case.
First, the tidal force is explicated in the
figure below
(local link /
general link: tidal_force.html).
Recall that by
rotating frames,
we mean those rotating relative to the
observable universe.
Rotating frames
are non-inertial frames,
but NOT simple ones.
Every small region in them over a short enough time scale is a simple
non-inertial frame
(i.e., a reference frame
accelerated relative to a local
inertial frame),
but overall they form a continuum of such simple
non-inertial frames.
Nevertheless, they can be converted to
inertial frames
easily in the
classical limit
by invoking 3
rotating frame
inertial forces:
the centrifugal force,
the Coriolis force,
and Euler force.
The Euler force is needed
for accelerated
rotating frames
and it is NOT needed for the
case of the Earth and we will
NOT discuss it further.
The centrifugal force
is that "force" that tries to throw you off
carnival centrifuges.
In the rotating frame,
it is an outward pointing
body force trying to throw every bit
of you outward and an ordinary
force has to be exerted on
you to hold you in position.
From the perspective of the
(approximate) inertial frame
of the ground,
you are just trying to move at a uniform
velocity
in a straight line per
Newton's 1st law of motion.
Both the centrifugal force
and the Coriolis force
are important in understanding the internal motions
of moons,
planets,
stars,
all other compact astro-bodies
(i.e., those NOT held up by kinetic energy)
since these are virtually always
rotating due to their
formation process.
More details on
rotating frames
are given below in the section
Rotating Frames Explicated.
For an important example of the
centrifugal force
at work, see the below section
The Centrifugal Force of the Earth's Rotation.
For important example of the
Coriolis force
at work, see the below section
The Coriolis Force of the Earth's Rotation.
An explication of the basics of
rotating frames
is given in the figure below
(local link /
general link: frame_rotating.html).
An explication of how the
figure of the Earth
is affected by the
centrifugal force
due to the Earth's rotation
is given in the figure below
(local link /
general link: earth_oblate_spheroid.html).
Almost all compact astro-bodies
(i.e., those NOT held up by kinetic energy,
including neutron stars
and black holes which
require relativistic physics)
are subject to the
the centrifugal force
(since they almost all are rotating
relative to the observable universe)
and
many to the tidal forces
(since many are located in relatively compact
systems
of astro-bodies).
These effects cause distortion from the perfect
spherical symmetry
of hydrostatic equilibrium
that the self-gravity
and pressure force
of an astro-body
try to create.
The centrifugal force
gives equatorial bulges
and the tidal force
to tidal bulges
which in general will be located in various complex ways.
If both centrifugal force
and tidal force are relatively
small compared to
astro-body's
self-gravity
and pressure force,
they can be treated as
perturbations
and their effects just added together.
If one or both are NOT relatively small, a more detailed treatment is needed.
For the Earth, both
centrifugal force
and tidal force are relatively small
although the centrifugal force
has a much bigger effect.
The equatorial bulge
(evidenced by the fact that the
Earth equatorial radius R_eq_⊕ = 6378.1370 km
and the Earth polar radius R_po_⊕= 6356.7523 km, and so there is a difference of 21.3847 km) is much larger than
the tidal bulges
(which for the water tide
in the open ocean have
a tidal range
∼ 1 m
and for the solid Earth tide
∼ 1 m also: see
Wikipedia: Tidal_range: Geography
Wikipedia: Earth tide:
Tidal constituents).
An explication of how
weather
is affected by the
Coriolis force
due to the Earth's rotation
is given in the figure below
(local link /
general link: coriolis_force.html).
The Foucault pendulum
and how it demonstrates the
Earth's rotation
relative to the
observable universe
is explicated the figure below
(local link /
general link: pendulum_foucault.html).
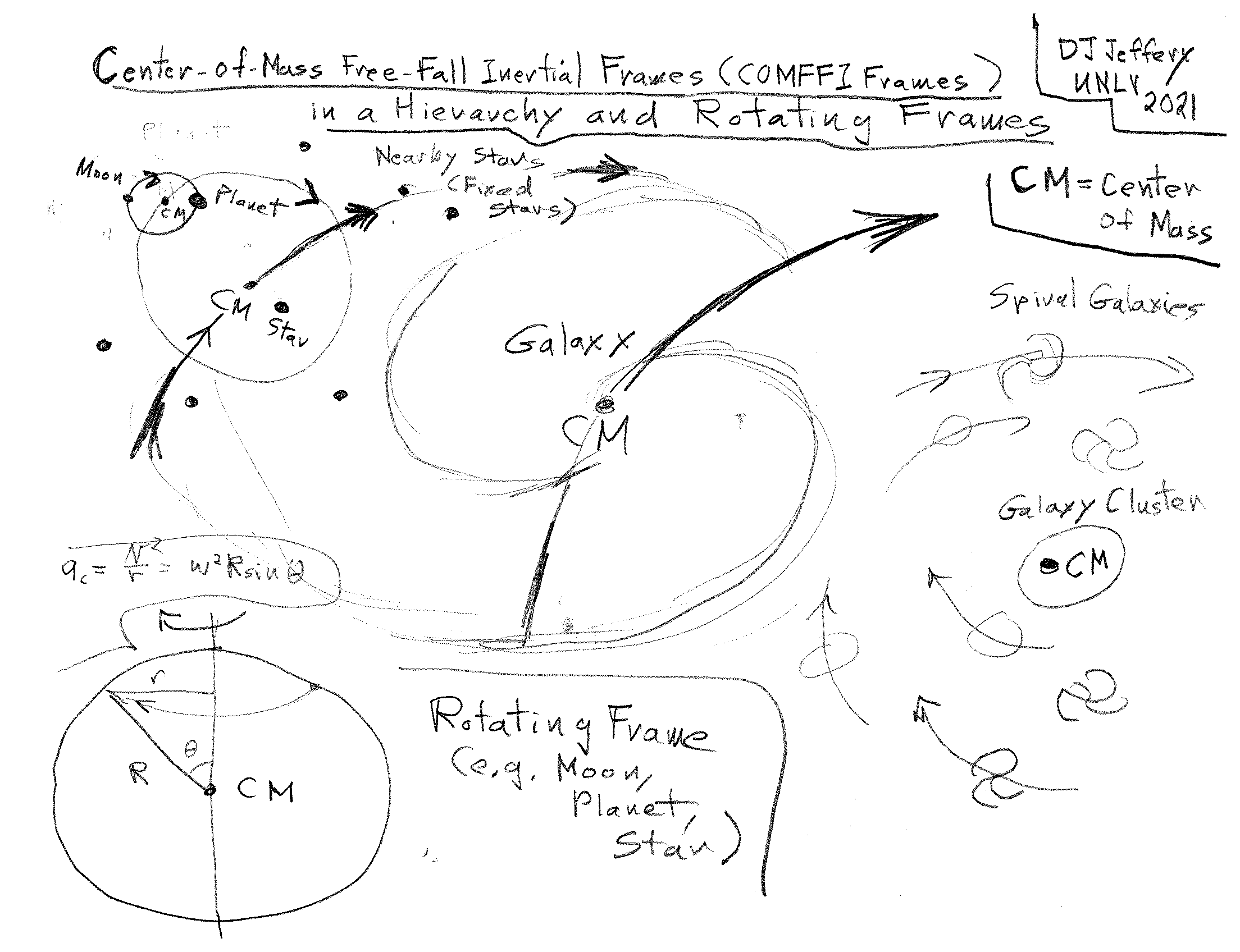
Astrophysical
center-of-mass frames
and their largest special case
comoving frames
are explicated in the the figure below
(local link /
general link: frame_hierarchy_astro.html.html).
All true theories
in physics are only exactly true
in ideal limits that can only be approached more or less closely in practice.
Reality just
has too many
degrees of freedom
to absolutely cleanly isolate
a theory from all complicating effects,
and, of course, NO
continuous quantity
can ever be measured exactly.
So inertial frames
(which follow from a theory in
physics) can NEVER be exact.
If an inertial frame is
exact enough for your purposes, then
you would just refer to it as
an inertial frame.
If it is NOT exact enough,
you could refer to it as an
approximate inertial frame.
For example any point on the
Earth's surface defines
a LOCAL inertial frame
that can be just called
an inertial frame
since it is an exact enough
inertial frame for most purposes.
It if is NOT quite exact enough for your purposes, you could call it
approximate inertial frame.
If you need a more exact
inertial frame,
you need to introduce appropriate
inertial forces.
We discuss the
inertial frames
and the Earth in the above section
Inertial Frames and the Earth.
CM inertial frames
(see above section
Center-of-Mass (CM) Inertial Frames)
are a good way to understand
reference frames
used in
astrophysics
in the classical limit.
To go beyond the
classical limit
requires
relativistic physics
(combined
special relativity (1905)
general relativity (1915)).
In the classical limit,
we use Newtonian physics
and certain restrictions apply:
The classical limit
sounds very restrictive, but, in fact, pretty much everything from
cosmic dust to
the
large scale structure
of the universe
can be analyzed as in the
classical limit to good to
excellent approximation
depending on the case.
Actually, the observable universe
as whole can be treated using
Newtonian physics
in that the
Friedmann equation
can be derived from
Newtonian physics
plus special hypotheses.
We will NOT go into that here.
The behavior of black holes and close to
black holes CANNOT
be dealt with by Newtonian physics,
but black holes from far enough
away from them can be treated as
point mass
sources of gravity
by Newtonian physics.
To conclude this section,
CM inertial frames
are very
general inertial frames
for celestial mechanics, but
they are NOT completely general.
Complete generality is beyond yours truly's scope of knowledge
and is probably unnecessary for understanding
most reference frames
used in astrophysics.
EOF
Newton's absolute space
was theorized by
Isaac Newton (1643--1727)
to be the singular fundamental
inertial frame
(and the one in which the
fixed stars
[which were all the
stars known in his age]
were at rest on average)
and only
reference frames
NOT accelerated relative to
Newton's absolute space
were
true inertial frames.
Now yours truly likes the perspective that
Newtonian physics
is a true emergent theory.
It is exactly true in the
classical limit.
But NOT
Newton's absolute space.
That was always a wrong theory.
However, old practitioners of
celestial mechanics
assuming
Newton's absolute space
from Newton
on until the advent of
general relativity
in 1915 and even a bit later (see below)
still got the right answers for calculations of celestial motions
of the systems
of astro-bodies they treated
(i.e., planet-moon systems,
the Solar System,
and multiple-star systems).
Why?
They treated
CM inertial frames
just the way we do, except they
could only use the
fixed stars
for measuring "absolute rotation" (as we discussed in
above section
Rotation Relative to the Observable Universe),
but that was adequate for their level of
accuracy/precision.
We still use the
fixed stars
for measuring "absolute rotation", except for the highest
level of accuracy/precision
for which we use
International Celestial Reference System
as we discussed in the
above section
Rotation Relative to the Observable Universe
to measure rotation relative to the
observable universe
(i.e., bulk mass
of the observable universe)
which is what yours truly means by "absolute rotation".
So all the calculations of the old practitioners of
celestial mechanics
got the same answers we do (except at the highest
level of
accuracy/precision)
for the
systems
of astro-bodies they treated.
Newton's absolute space
was an adequate
theory for their purposes.
However, the old practitioners could NOT have done modern
cosmology
without the modern understanding of
CM inertial frames
since they could NOT have understood the
expansion of the universe
with
Newton's absolute space.
Actually,
Newton himself
partially understood
that Newtonian physics
was inadequate for cosmology
(see No-374--377).
Now Newton and those
other old practitioners of
celestial mechanics
could equally well have anticipated
the general relativity
perspective of ideal
inertial frames
(see the above section
Ideal Inertial Frames)
which is the correct one for the
observable universe,
but they did NOT do so.
If they had, they might have been able to derive some of
modern cosmology.
The theory of
Newton's absolute space
continued to be held by some up to the
1920s it seems.
The observational discovery of the
expanding universe
in 1929
by Edwin Hubble (1889--1953)
and its theoretical understanding in terms of the
Friedmann-equation (FE) models
derived from
general relativity
caused
Newton's absolute space
to be thoroughly and most sincerely discarded.
Recall
the center of mass
of any body is its
mass-weighted
average position
(see Wikipedia:
Center of mass).
Second, the tidal force and
Earth are discussed
in the figure below
(local link /
general link: tide_earth.html).
For the thrill of it all, see the video
Alien Abduction gravitron ride
at Bluegrass Fair Lexington (June 19th, 2021) | 2:14.
The Coriolis force is a bit trickier
and arises when you have
velocity relative to
a rotating frame.