Caption: An animation dynamically illustrating a rotating frame (attached to a DISK) whose center is at rest relative to a simple EXTERNAL inertial frame (i.e., an EXTERNAL inertial frame NOT rotating relative to the observable universe).

The ball in the animation is sliding frictionlessly on the DISK and NO ORDINARY forces are acting on it at all, and so there is NO net ORDINARY force acting on it.

The left-hand panel gives the EXTERNAL inertial frame perspective and the right-hand panel gives the rotating frame perspective.

Below, we give an introduction to the basics of rotating frames. Our discussion mostly assumes the classical limit where Newtonian physics applies and relativistic effects are vanishingly small. Occasionally, relativistic effects are mentioned, but a full discussion of them is beyond our scope.

Features:

1. A simple non-inertial frame is one in uniform acceleration relative to an inertial frame.

   The non-inertial frame can be converted into an inertial frame by the introduction of the simple inertial force "-ma" where "m" is the mass of any object under consideration and "a" is the uniform acceleration of the simple non-inertial frame.

   Inertial forces are body forces that act equally per unit mass on all bits of a body.

   So if a body does NOT resist inertial forces, it suffers NO deformation/strain.

   In the classical limit, one can view the introduction of inertial forces as way of generalizing Newton's laws of motion to non-inertial frames.

   You do NOT introduce inertial forces at all if you are using an inertial frame right from the beginning of an analysis.

   However, the perspective of the conversion of non-inertial frames to inertial frames is extremely useful in many cases. For important example, rotating frame which we are consideriong in this figure.

   Note, the conversion of an non-inertial frames to an inertial frame is NOT just a trick. An axiom of general relativity is that almost all physical laws are referenced to inertial frames whether they are simple inertial frames or converted inertial frames. Thus, there is a fundamental likeness of all inertial frames.

   General relativity itself is NOT referenced to inertial frames and, in fact, tells us what they are.

   One can quibble about whether there are other physical laws NOT referenced to inertial frames, but yours truly thinks the quibbling is a matter of perspective or may amount to saying you are NOT using inertial frames in some definitional sense when effectively you are using them.

2. A rotating frame (in the sense we mean in this discussion) is one in absolute rotation (i.e., in rotation relative to the observable universe: i.e., to the bulk mass-energy of observable universe) (see Wikipedia: Inertial frame of reference: General relativity).

3. Now a rotating frame is an non-inertial frame, but NOT a simple non-inertial frame (see discussion above). In fact, it is a continuum of simple non-inertial frames each with time-varying acceleration relative to an EXTERNAL inertial frame.

   However, by convention, a rotating frame is considered one non-inertial frame. It certainly is one reference frame.

4. Now there is a formalism to convert a rotating frame into an inertial frame. Below, we explicate this formalism and the animation.

   But first note that to avoid tedious and unenlightening generality, we will limit our discussion to rotating frames where the rotation axis does NOT have axial precession relative to the observable universe and is at rest relative to an EXTERNAL inertial frame. We also limit ourselves mostly to rotating frames that have constant angular velocities. These limitations can all be relaxed if one needs to.

   The animation conforms to our limitations.

   A extreme example of the kind of rotating frame we are NOT discussing is one rotating relative to another rotating frame, but NOT rotating relative to the observable universe. Such tricky cases have their interest, but are finicky to discuss.

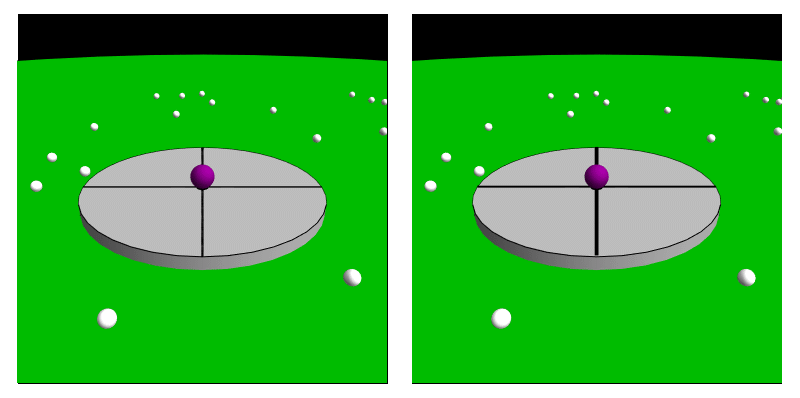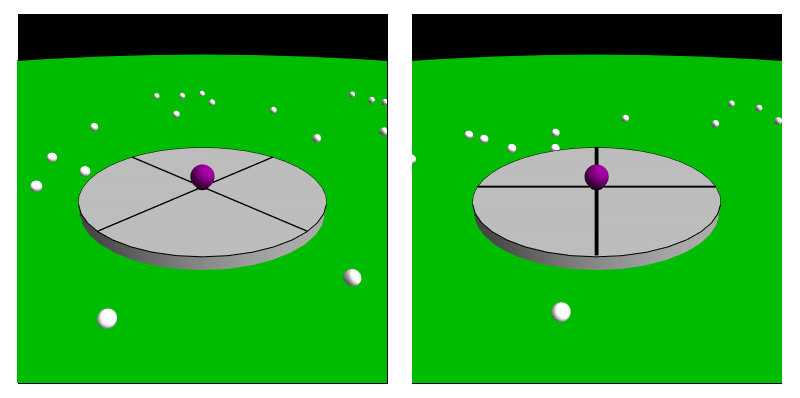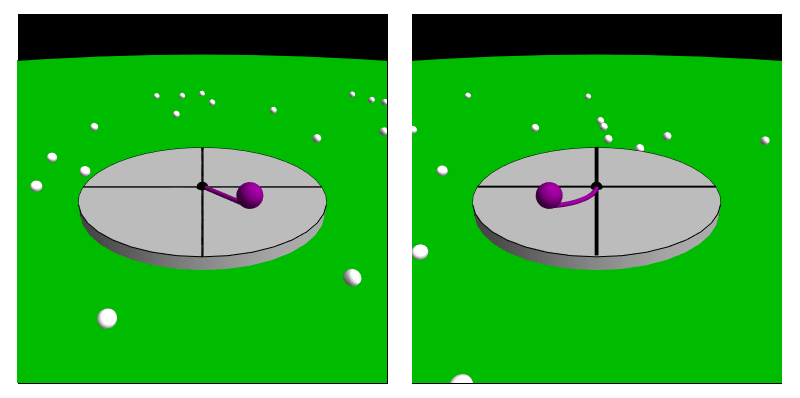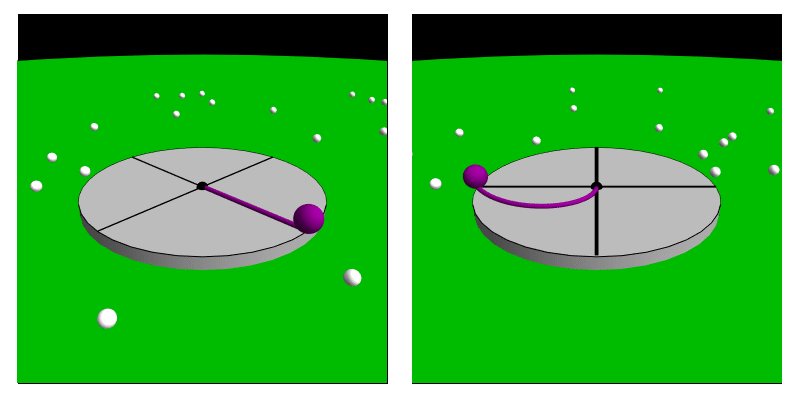
5. In the animation, the left-hand panel shows the ball's motion relative to the EXTERNAL inertial frame. It moves in a straight line at a constant speed, and so is unaccelerated---it's in uniform linear motion. By Newton's 2nd law of motion (AKA F=ma), there is NO ORDINARY net force on the ball as aforesaid.

   Recall Newton's laws of motion are referenced to inertial frames although this essential fact is often omitted in high-school presentations.

6. The right-hand panel shows the ball's motion as seen by an observer in the rotating frame. The ball has an accelerated motion since it follows a curved path despite have NO ORDINARY net force acting on it. But there is NO violation of the Newton's 2nd law since the rotating frame is a non-inertial frame.

   But, as aforesaid, we can convert non-inertial frames to inertial frame by introducing inertial forces.

7. The conversion of a rotating frame (whose center is at rest in an EXTERNAL inertial frame) to an inertial frame is effected by the introduction of 3 rotating frame inertial forces:
   1. The centrifugal force which is easy to understand. It's just the force that tries to throw you off carnival centrifuges. From the outside EXTERNAL inertial frame of the ground, you are just trying to move in a straight line at a constant speed in accordance to Newton's 1st law of motion and the force on your back by the carnival centrifuge is needed to accelerate you with the rotating frame of the carnival centrifuge. In general, if you try to stay in one place in the rotating frame, you have to exert real forces to hang on to the rotating frame and stay at rest relative to it.

      For the thrill of it all, see the video Alien Abduction gravitron ride at Bluegrass Fair Lexington (June 19th, 2021) | 2:14.

   2. The Coriolis force is trickier to understand. It is a velocity-relative-to-the-rotating frame-dependent force. It depends linearly on the relative relative velocity. If you are NOT moving relative to the rotating frame, the Coriolis force is zero. The Coriolis force is important in weather phenomena in the rotating frame of the Earth's rotation. It's the cause of the vortex motion of cyclones (see Wikipedia: Cyclone: Structure) and anticyclones (see Wikipedia: Anticyclone: Structure). See more explication of cyclones and anticyclones in Mechanics file: coriolis_force.html. The Coriolis force also affects long-range artillery ballistics. We do NOT ordinarily notice the Coriolis force of the Earth's rotation on smaller scales than weather and long-range artillery ballistics. However, on human size scale, Coriolis force causes the behavior of a Foucault pendulum. For an explication of the Foucault pendulum, see Mechanics file: pendulum_foucault.html.

   3. The Euler force which arises if the rotation of a rotating frame is accelerating.

8. The ball in the animation is affected by the centrifugal force and Coriolis force, but NOT by the Euler force since the rotation of the DISK is NOT accelerating.

   The main reason the ball follows a curved path in the animation is the Coriolis force since the ball has velocity relative to the rotating frame of the DISK.

9. All the rotating frame inertial forces arise in playground merry-go-rounds: see the figure below (local link / general link: merry_go_round.html).

   ---

10. For more illustrations of motions in inertial frames and non-inertial frames, see Inertial frames and non-inertial frames videos below (local link / general link: frame_videos.html).

    EOF