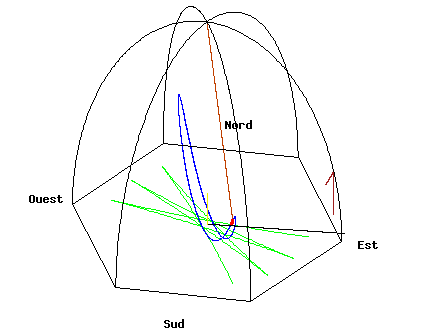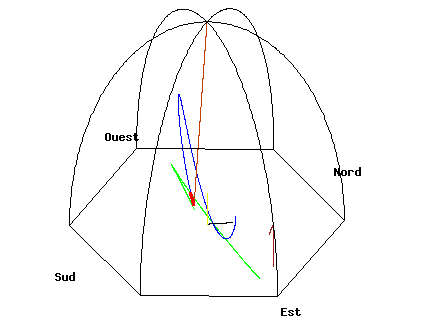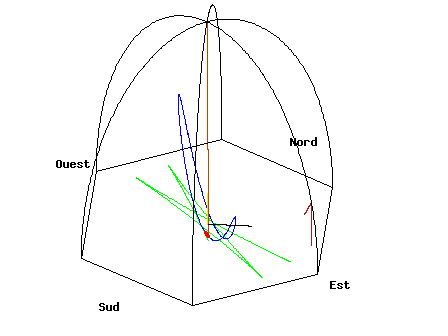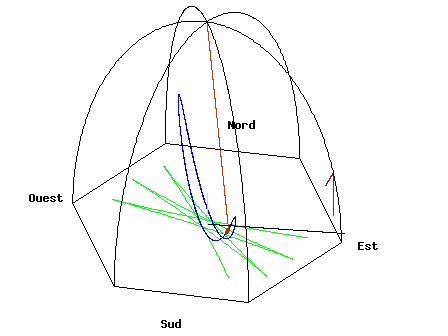
Image 1 Caption: An animation of a Foucault pendulum showing the counterclockwise rotation of its plane of oscillation (which effectively sweeps out a cone) in the Southern Hemisphere. The animation is time-lapsed: an actual rotation period is longer than a sidereal day = 86164.0905 s = 1 day - 4 m + 4.0905s (on average).

Features:

1. The non-rotation of all (or almost all) free-fall frames (which are exact inertial frames according to general relativity (GR) via the strong equivalence principle) relative to the in-theory non-rotating reference frame of the observable universe to very high accuracy/precision (or relative to the fixed stars to good approximate accuracy/precision) can be observed on Earth with a Foucault pendulum: a pendulum where the pivot can turn freely with negligible friction in any direction. Because of its free pivot, a Foucault pendulum CANNOT be torqued around its vertical axis by its pivot, and so CANNOT be torqued around its vertical axis by the Earth to which the pivot is attached.

   Note that very strong gravitational fields (like those very near black holes) may cause the rotation of free-fall frames relative to the reference frame of the observable universe, but this is a tricky point for which yours truly cannot find a clear explication. The best so far (and it does NOT say much) is Wikipedia: Inertial frame of reference: General relativity.

2. Foucault pendulum is, in fact, a way to demonstrate that Earth surface locations are NOT inertial frames on the small size scale.

   Large size scale non-inertial frame effects are evidenced by weather (particularly anticyclones and cyclones), long-range artillery ballistics, and the tides.

3. The simplest locations for a Foucault pendulum are at the poles. There a Foucault pendulum swings in a plane fixed relative to the observable universe (or fixed stars to good approximate accuracy/precision) which means a plane that rotates relative to the relative to the Earth once per sidereal day (to good approximate accuracy/precision).

4. The second simplest location is the equator where the plane of oscillation does NOT rotate at all relative to the Earth.

5. The general formula for the rotational period of a Foucault pendulum is

   P = (1 sidereal day) / sin(L) ,

   where L is latitude. Note that sin(L=90°) = 1 gives P = 1 sidereal day and sin(L=0°) = 0 gives P = ∞ which means NO rotation.

   In the Northern Hemisphere (Southern Hemisphere), the rotation is clockwise (counterclockwise): see Wikipedia: Foucault pendulum: Explanation of mechanics.

   The animation shows counterclockwise rotation because it is for the Southern Hemisphere.

6. An image of Leon Foucault (1819--1868) is in the background of the animation. Foucault used a Foucault pendulum (which he did NOT invent) to demonstrate the Earth's rotation relative to the fixed stars in 1851 (see Wikipedia: Leon Foucault: Middle years; Wikipedia: Pantheon: Under Louis Philippe I, the Second Republic and Napoleon III (1830-1871)). The Foucault pendulum was a huge one in the dome of the Pantheon in Paris.

   

7. Image 2 Caption: An animation of illustrating a Foucault pendulum located in the dome of the Pantheon in Paris. This Foucault pendulum (although maybe NOT Foucault's Foucault pendulum) has length 67 meters and is released at a distance of 50.25 meters (3/4 its length) in the east with a zero speed. The Earth's rotation is time-lapsed to 110 seconds. Alas, the original caption is rather incomplete.

Images:

1. Credit/Permission: Dominique Toussaint (AKA User:DemonDeLuxe), 2006 / CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:Foucault pendulum animated.gif.
   
2. Credit/Permission: User:Nbrouard, 2007 / CC BY-SA 3.0.
   Image link: Wikimedia Commons: File:Foucault-rotz.gif.