Image 1 Caption: Alexander Friedmann (1888--1925) serving as an aviator in Imperial Russian Air Service, Imperial Russian Army, World War I (1914--1918), 1916 Aug01. A Russian-Soviet aviator, ballonist, mathematician, meteorologist, physicist, pioneering cosmologist, and discoverer of the eponymous Friedmann equation in 1922. See also Wikipedia: Alexander Friedmann and The MacTutor History of Mathematics archive: Aleksandr Aleksandrovich Friedmann.

Features:

1. Starting from the Einstein field equations of Albert Einstein's (1879--1955) general relativity, Friedmann in 1922 derived 2 differential equations that describe the behavior of a homogeneous, isotropic universe consisting of a perfect fluid. Being homogeneous and isotropic means the universe obeys the cosmological principle.

2. The first of the differential equations is now called Friedmann equation and the second, the acceleration Friedmann equation (or just the other Friedmann equation).

   The Friedmann equation is

   [(da/dt)/a]**2 = (8πG/3)ρ - k/a**2 + Λ/3    ,

   where "a" is the cosmic scale factor a(t), "t" is cosmic time, "G" is gravitational constant G = 6.67430(15)*10**(-11) (MKS units), "k" is the curvature (k > 0 for positive curvature space, k < 0 for negative curvature space, k = 0 for Euclidean (i.e., flat) space), and "Λ" is the cosmological constant (AKA Lambda, AKA Λ).

   The cosmic scale factor a(t) is the solution of the Friedmann equation. But which solutions you obtain depend on the ingredients (including free parameters) you insert into the Friedmann equation.

   Solutions of the Friedmann equation for the cosmic scale factor a(t) that are historically interesting are often called universes: e.g., the Einstein universe (1917) and the de Sitter universe (1917).

   

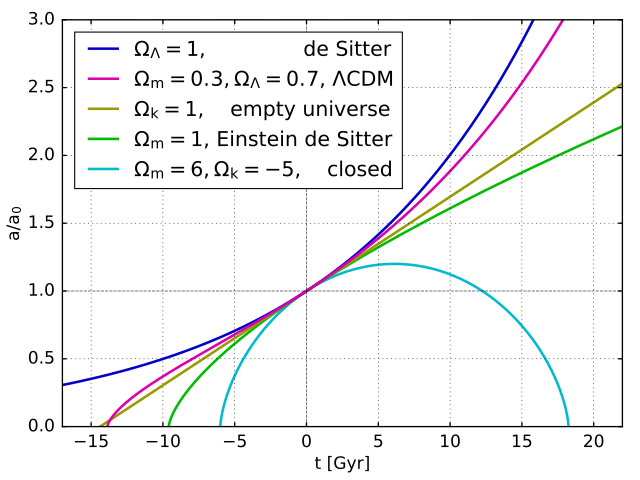
3. Image 2 Caption: Examples of interesting cosmic scale factor solutions a(t): the de Sitter universe (1917), the Λ-CDM model (the standard model of cosmology (SMC) since circa 1995: e.g., Scott 2018, p. 10), Einstein-de Sitter universe (1932) (which is NEITHER the Einstein universe (1917) NOR the de Sitter universe (1917)), a linear growth solution (e.g., the empty universe or Rh=ct universe (2011)), and the positive curvature universe (AKA closed universe).

4. The Friedmann equation is derived from general relativity along with 2 of Einstein's original assumptions which are discussed in section IAL 30: Einstein, General Relativity, and the Einstein Universe (see also No-524--527): i.e., the cosmological principle and the representation of the mass-energy of the universe by a homogeneous, isotropic, perfect fluid (in older astro jargon the cosmic substratum: Bo-75--76).

   A zero or non-zero cosmological constant Λ can be included in the Friedmann equation, and so in the FE models.

   However, a key point of the FE models is that in all cases they give NON-STATIC solutions---unless cosmological constant Λ to adjusted to exactly the right value to give the Einstein universe (and analogue cosmological models). Other than the Einstein universe case (and analogue cosmological models), the FE models must expand or contract---and they do this maintaining the cosmological principle.

5. The dynamics of the FE models is determined by the gravity and the inertia of the mass-energy and, if non-zero, the cosmological constant.

   

6. Image 3 Caption: Albert Einstein (1879--1955), master of the universe.

   Einstein is seen here, chalk in hand, lecturing in Vienna, Austria in 1921.

   In the days when he was the supreme master of physics.

7. Note Einstein derived the Einstein universe (1917) without having the Friedmann equation by a klutzy process which he described as "a road long and painful"---"eine weg langhaft und traurig" (see, e.g., O'Raifeartaigh et al. 2017, p. 18). Likewise Willem de Sitter (1872--1934) derived the de Sitter universe (1917) without having the Friedmann equation by a klutzy process.

   If either of them had discovered the Friedmann equation, it would have saved them a lot of work and would have clarified general relativistic cosmology several years earlier than in actual history.

8. In 1924, Friedmann developed some of the models based on the Friedmann equation that we call collectively the Friedmann-Lemaitre-Roberston-Walker (FLRW) models. However that name is so cumbersome that yours truly just abbreviates it to FE models for Friedmann equation models.

9. The FE models predict the expansion of the universe and Hubble's law---which Edwin Hubble (1889--1953) discovered observationally in 1929.

10. The Friedmann equation and the acceleration Friedmann equation are collectively one of the bases of the modern-day cosmology.

11. Big Bang cosmology includes the Friedmann equation models and the Λ-CDM model (our current standard model of cosmology (SMC, Λ-CDM model)) which is a Friedmann equation model.

    

12. Image 4 Caption: Georges Lemaitre (1894--1966) between Robert Millikan (1868--1953) and Albert Einstein (1879--1955) at Caltech, 1933 Jan10.

13. Actually, Friedmann's results were NOT well known outside of Russia in the 1920s---maybe NOT even in it. And, in fact, Georges Lemaitre (1894--1966) independently rediscovered Friedmann's results which he reported in 1927.

14. Lemaitre in his report of 1927 also explicitly discovered Hubble's law as theoretical prediction of the FE models (which Friedmann must have known, but never explicitly published). To emphasize, this is the discovery of Hubble's law as theoretical prediction, NOT a discovery that the observable universe obeyed Hubble's law:

      v=H_0*r  ,

    where "v" is recession velocity from the Milky Way, "H_0" is the Hubble constant H_0 = [(70 km/s)/Mpc]*h_70, h_70 = H_0/[(70 km/s)/Mpc], and "r" is proper distance (i.e., distance that can be measured with a ruler at one instant in cosmic time) from Milky Way. Note that in general "v" and "r" are NOT direct observables, but they become direct observables as asymptotically as r→0, and so "H_0" can be directly measured.

    Moreover, Lemaitre was able using published data on galaxies to find values for the Hubble constant (575 (km/s)/Mpc or 670 (km/s)/Mpc: Way 2013, p. 14) that were relatively close to what Hubble found in 1929 (500 (km/s)/Mpc: Hubble 1929, 3rd to last paragraph; Bo-39; Tamann 2005; Wikipedia: Timeline of Hubble constant values). In fact, both Lemaitre's and Hubble's Hubble constant values are too large by a large factor because of a large calibration error and other measurement uncertainties. Actually, Hubble constant = 70 (km/s)/Mpc (fiducial value accurate to within ∼ 10 %).

    To emphasize, Lemaitre did NOT discover that the observable universe obeyed Hubble's law with his Hubble constant, but that if the observable universe obeyed Hubble's law and one used the data he used (which had as aforesaid a large calibration error and other measurement uncertainties), then the Hubble constant had the values he found.

    Lemaitre did publish his results in 1927 as aforesaid, but they did NOT attract much interest and it seems likely that he did NOT wish to get into a piority dispute with Hubble, and so he did NOT emphasize to his pre Edwin Hubble (1889--1953) Hubble's law work.

    However, in 2018, the IAU decided to give Lemaitre some credit and formally changed the name of Hubble's law from Hubble's law to the Hubble-Lemaitre law. Yours truly does NOT think the longer name will be much used. We've always called Hubble's law Hubble's law and it's shorter to say and write.

Images:

1. Credit/Permission: Anonymous photographer 1916 (uploaded to Wikimedia Commons Wikipedia by User:Ctac, 2015) / Public domain.
   Image link: Wikimedia Commons: File:Fridman AA.jpg.
   
2. Credit/Permission: © User:Greek3, 2017 / CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Mplwp universe scale evolution.svg.
   
3. Credit/Permission: Ferdinand Schmutzer (1870--1928), 1921 (uploaded to Wikipedia by User:Hemulen, 2006) / Public domain.
   Image link: Wikipedia: File:Einstein_1921_by_F_Schmutzer.jpg.
   
4. Credit/Permission: Anonymous photographer, 1933 / Public domain very probably.
   Image link: Universite Catholique de Louvain: Georges Lemaitre Archives.