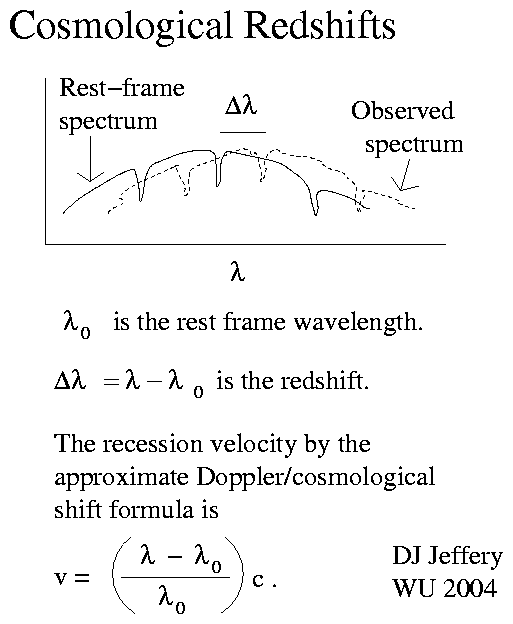
Cosmological Redshift Topics:
Note, the increase in
wavelength is NOT
a forced stretching.
Energy is NOT being
put into the EMR.
It's actually being taken out.
For an explication, see topic
Cosmological Redshift and Energy Conservation below.
The cosmic scale factor
for cosmic present t_0 (equal
to the age of the observable universe = 13.797(23) Gyr (Planck 2018))
is conventionally set to 1 and given symbol a_0.
Note, subscript 0 indicates
cosmic present by usual convention.
Thus, a(t=t_0) = a_0 = 1.
Cosmic time is measured from
Big Bang which
happened at
lookback time the
age of the observable universe = 13.797(23) Gyr (Planck 2018)
(see Planck 2018: Age of the observable universe = 13.797(23) Gyr).
Note, from our understanding of
general relativity (GR),
the scaling up with
cosmic scale factor a(t)
is a literal growth of
intergalactic space.
From our understanding of
the cosmic scale factor
(which we further explicate below in section
The Cosmic Scale Factor),
the wavelength of
EMR signal (or,
in the quantum mechanical perspective,
a photon)
propagating through
intergalactic space
just scales with a(t): i.e.,
Since cosmological redshift z
is a direct observable, the
relative cosmic scale factor a_0/a(t)
is a direct observable.
Just add 1 to z and we get it.
But we do NOT get cosmic time t!!!!!
The fact is that a(t)'s functional dependence on
cosmic time t is
NOT known observationally: it is a
function
dependent on the
cosmological model.
So the scaling-up formula does NOT
give us t or lookback time
which is t_0-t.
If we did have
cosmic time t,
we'd easily be able to determine the
cosmic scale factor a(t)
throughout most of
cosmic time and
cosmology would be a lot easier.
If only galaxies had
clock faces on them that told
cosmic time, but they do NOT.
In fact, solving for
cosmic scale factor a(t)
from the Friedmann equation
of cosmology
(which is derived from
general relativity
along with certain assumptions) is one of the main goals
of cosmology.
With the atom or
molecule identified,
one does know all the intrinsic
line wavelengths
(i.e., the λ's) and
then the cosmological redshift z
can easily be calculated from
the above formula
z = (λ_0 - λ)/λ using the
observed wavelengths
(i.e., the λ_0's).
They can only be known in general from
a cosmological model
fitted to the
observable universe.
Since circa 1998
to circa 2020????,
the standard model of cosmology (SMC)
has been the
Λ-CDM model
which fits all observations of
the observable universe
pretty well.
It may need revision or replacement in the near future,
but even so its predictions for
physical distance
and lookback time
will probably still be pretty accurate.
Thus, astronomers
would usually say
galaxy X is at
redshift z_X.
They are DIFFERENT, though closely related,
phenomena and their
general formulae
are DIFFERENT.
Doppler shift
is the shift in wavelength
due to relative velocity
in one inertial frame
or between two
inertial frames
in relative acceleration.
The situation is actually a bit complex in general for
EMR:
see
Wikipedia: relativistic Doppler effect.
Cosmological redshift,
on the other hand is a shift
wavelength due to
propagation through a
continuum
of inertial frames
that are separating due to the
expansion of the universe.
Note, the cosmological redshift
can be derived from the
Doppler shift
(see Li-38), but
in the opinion of yours truly that does
NOT make it
Doppler shift in any simple sense---to
repeat, the general formulae
are DIFFERENT.
However, many people are less finicky and call the
cosmological redshift a
Doppler shift.
The peculiar velocities
give real Doppler shifts
that have to be "subtracted off" the actually observed z to get the
cosmological redshift z.
For large cosmological redshifts,
the Doppler shifts are negligible, but
when you get very close to the
Milky Way, the
Doppler shifts dominate and
a correction is needed to get the
cosmological redshift z.
Inside the Milky Way,
it is usually pointless to consider the
cosmological redshifts
at all.
In intro astronomy courses, we do NOT worry about the complication of
Doppler shift
correction, but it is important.
In astro jargon,
the non-ordinary velocities
between
comoving frames
are called
recession velocities.
Recession velocities
do exceed the
vacuum light speed c = 2.99792458*10**8 m/s
(exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns
as you go to high
cosmological redshift z
(i.e., to cosmologicallly remote
proper distances).
But this is NOT a violation of
special relativity
since recession velocities
are between inertial frames
NOT relative to a local
inertial frame.
In fact, those who understood
Willem de Sitter's (1872--1934)
de Sitter universe (1917)
did understand the difference between
the cosmological redshift
and the Doppler effect.
Edwin Hubble (1889--1953) who made the
observation discovery of the
expansion of the universe
in 1929 was probably one of those who
did understand the difference.
Solving for it
from the Friedmann equation
of cosmology
(which is derived from
general relativity
along with certain assumptions) is one of the main goals
of cosmology.
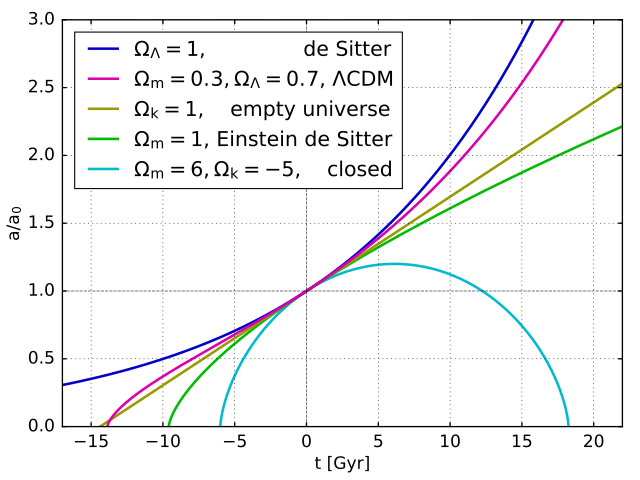
Image 4 below presents the
cosmic scale factor a(t)
for fiducial cosmological models.
But where does that lost energy go.
We believe in
energy conservation
(as exemplified by an ideal
Newton's cradle),
right?
This ideal Newton's cradle
exhibits exact
conservation
of mechanical energy since NO
mechanical energy
is dissipated
to waste heat
by friction,
air drag,
or any other process.
Mechanical energy
is the sum of kinetic energy
and
gravitational potential energy
in this case.
It just vanishes
(see Car-120).
It's somewhat distressing that
energy conservation
in the ordinary sense
does NOT hold necessarily according to
general relativity.
But all is NOT lost.
General relativity
gives us a generalization of
ordinary energy conservation:
the
general-relativity energy-momentum conservation equation
(see also Car-120).
Which equation we will NOT go into here.
We just have to note that in certain
contexts (which do NOT occur in
everyday life NOR
in most of astrophysics)
ordinary
energy conservation
does NOT hold.
The
cosmological redshift
is one of those cases.
Another case is
gravitational waves.
Gravitational waves
do convey energy
and momentum
across spacetime,
but there is NO general proof that
they conserve these quantities
as they propagate across spacetime
though there is a special case proof for
energy conservation and
momentum conservation
which gives what is called
the Bondi-Sachs energy-momentum conservation law
(see
Roger Penrose, The Road to Reality, 2004,
p. 467--468).
But what about
gravitational waves
in an expanding universe.
Surely, their
wavelength increases
as they propagate, but do they
lose energy thereby?
We need a great expert to tell us.
Another interesting point about
gravitational waves
is that they make NO contribution to the
energy-momentum tensor T_ij
of the Einstein field equations.
So though they convey
energy
and momentum
across spacetime,
there is NO way to assign so much
energy density
to any point in the
gravitational waves.
Somehow the
energy
is coded into the
gravitational waves
in a non-local way
(see
Roger Penrose, The Road to Reality, 2004,
p. 467--468).
For more on the
non-local gravitational field energy,
see Relativity file:
non_local_grav_field_energy.html.
The description here should be conflated with the description that file someday.
λ_0 = [a_0/a(t)]λ ,
where λ is the initial wavelength
of emission,
t is the cosmic time of emission,
and λ_0 is the wavelength
at cosmic present t_0
(equal to the age of the observable universe = 13.797(23) Gyr (Planck 2018)).
λ_0 - λ a_0
z = ------- = ---- - 1 .
λ a(t)
We see that the
cosmological redshift
is the relative change in
wavelength from emission to observation.
a_0/a(t) = z + 1 or inverting to get a(t) = a_0/(z+1) ,
where a_0 = a(t_0): i.e., the
cosmic scale factor
at cosmic present t_0
= to the age of the observable universe = 13.797(23) Gyr (Planck 2018)
which conventionally we set to 1.
z = Δλ/λ = v/c << 1 ,
where Δ = (λ_0-λ),
λ is either of λ_0 or λ since they are the same
to 1st-order,
and v is
relative velocity
along the
line of sight)
between emitter and observer.

Images:
Local file: local link: cosmological_redshift.html.
Image link: Itself.
Image link: Wikipedia:
File:Wave packet (no dispersion).gif.
Image link: Wikipedia:
File:Two redshifts.JPG.
Image link: Wikimedia Commons:
File:Mplwp universe scale evolution.svg.
Image link: Wikimedia Commons:
File:Newtons cradle animation book 2.gif.
File: Cosmology file:
cosmological_redshift.html.