- Introduction
-
In this IAL,
we vanish into the black hole.
For a preview, see the figure below
(local link /
general link: black_hole_accretion_disk.html).
However, before that catastrophe, we need a brief introduction to special relativity (see see Special Relativity) and general relativity (see section General Relativity). General relativity is also needed for cosmology in IAL 30: Cosmology.
- Special Relativity (Reading Only)
-
Special relativity
was presented by
Albert Einstein (1879--1955) in
1905.
For Himself,
see the figure below
(local link /
general link: einstein_clerk.html).
-
The Postulates of Special Relativity:
Special relativity was derived Einstein in a physicsy way, NOT a mathematically rigorous, way. In the physicsy way, one introduces extra minor extra postulates (AKA axioms) that seem reasonable as one goes along in the derivation.
There are, however, 2 main basic postulates of special relativity: the postulates of special relativity:
- The Relativity Postulate:
The relativity postulate states that the laws of physics should be the same in all inertial frames. To be a bit more explicit, in all local inertial frames (i.e., all inertial frames at the same point in space, but differing in velocity).
The above is the same as saying the formulae that express the laws of physics should be the same in all inertial frames: i.e., the formulae should be inertial-frame invariant.
-
Note, the values of the variables
that go into the formulae
change with inertial frames:
e.g., the value of velocity.
But the variables should NOT: e.g., if the variable
velocity is intrinsically in a
physical law formula, it should
be in that formula always in the
same way.
This understanding of inertial frames was NOT known, even to Einstein, until general relativity was fully discovered in 1915. However, the understanding people had in 1905 was adequate for understanding special relativity.
-
General relativity
itself falls into a special category since it gives us our modern understanding
of inertial frames,
and so itself NOT referenced or
inertial frames
or from another perspective tells us all
local reference frames are
local inertial frames
when one deals with them in the right way.????
-
No one was taking polls about the opinions of
physicists circa
1905, and so we can only make educated
guess about what they mostly thought.
- Transformation Between Frames:
Now how are formulae transformed between inertial frames?
With transformation formulae.
The Galilean transformations (which we will NOT detail here) are the classical way of changing from one inertial frame to another: they were accepted almost without question from the time of Isaac Newton (1643--1727).
For example, the Galilean transformations are used to transform velocity between reference frames: e.g., the velocity of bicycle relative to the ground to its velocity relative to a passing car.
Note, particular velocities are NOT physical laws, and so are NOT required to be invariant under transformations between inertial frames.
The figure below (local link / general link: frame_transformations.html) illustrates transformations between inertial frames.
- Galilean Transformations and Lorentz Transformations:
Now Newtonian physics (i.e., its formulae) is inertial-frame invariant under the Galilean transformations and obeys the relativity postulate if the Galilean transformations are right.
But classical electromagnetism did NOT seem to obey the relativity postulate (as aforementioned) and this was because it was NOT inertial-frame invariant under the Galilean transformations.
-
Classical electromagnetism
is just the ordinary
theory of electromagnetism
which has been found extremely
adequate for macroscopic electric and magnetic phenomena and applications:
e.g., circuitry,
radio,
etc.
It's a true emergent theory: i.e., a theory that is true in a certain limit or regime.
-
Classical electromagnetism is
the macroscopic scale limit
of quantum electrodynamics (QED)---which
is a story for another day.
By "wrong", we mean less fundamental (except in an emergence sense) than the rest of classical physics. All of classical physics gave right answers for most phenomena known in 1905. There were some increasingly embarrassing anomalies---which we will NOT go into those here.
Most people then guessed it was classical electromagnetism that was less fundamental.
Einstein reasoned---based on reasons we will NOT go into here---that it was the Galilean transformations and Newtonian physics that were less fundamental than classical electromagnetism---and he was right.
Now classical electromagnetism was already known to be inertial frame invariant under the Lorentz transformations.
So Einstein reasoned that the Lorentz transformations were correct despite their weirdnesses (e.g., of making rate of time flow inertial frame dependent).
To maintain both the relativity postulate and classical electromagnetism, Einstein adopted the Lorentz transformations as true and went on to discover to discover a new physics: i.e., special relativity. He also needed another postulate for special relativity---which we give just below in subsubsection Light Speed Invariance Postulate.
- Galilean Transformations and Lorentz Transformations:
- Light Speed Invariance Postulate:
The light speed invariance postulate states that the vacuum light speed c = 2.99792458*10**8 m/s ≅ 3*10**8 m/s =3*10**5 km/s ≅ 1 ft/ns is the same for all local inertial frame observers regardless of how they are moving.
-
The vacuum light speed
also is the fastest physical speed relative to a local
inertial frame: i.e.,
the fastest speed that information or any effect can propagate
relative to a local
inertial frame.
This fact was deduced as
special relativity
was being derived from extra minor
postulate that
time travel to the
past was impossible since it is never
seen and presents
paradoxes that only
scifi can solve.
Note, time travel to the
future does happen as exemplified
by the twins paradox
(see subsection The Twins Paradox below).
Now the light speed invariance postulate upsets our usual ideas of relative motion. See the figure below (local link / general link: relativity_light.html) for an explication of the upset.
In formulating the light speed invariance postulate, it is NOT clear how aware Einstein was of the Michelson-Morley experiment (1887) (see figure below: local link / general link: michelson_morley_aether.html) experimentally showing the invariance of vacuum light speed to within experimental error. He said different things at different times and perhaps did NOT exactly remember in his later years.
By the by, the light speed invariance postulate has continued to be verified by experiment to the present day.
- Transformation Between Frames:
Note, the two special relativity postulates are continually verified by the verification of all the consequences of the special relativity since they all depend on those postulates.
- Salient Features of Special Relativity:
We will NOT derive special relativity from the special relativity postulates and NOT detail it here. But we will just discuss a few of its salient features:
- Weirdnesses of Special
Relativity Relative to Everyday Life:
The weirdnesses of special relativity are pretty much unnoticeable at relative speeds much less than the vacuum light speed. They vanish asymptotically as relative velocities go to zero and you approach the classical limit. On the other hand, they increase in size as relative velocities increase.
So this is why we do NOT ordinarily notice SPECIAL RELATIVISTIC EFFECTS.
But they can be measured by precise measurements---and they have been.
-
Of course, we do notice in that
the vacuum light speed
and light speed in media
are seemling close to infinite
in everyday life.
But we are used to this, and so do NOT consider it weird.
- The Vacuum Light Speed:
The vacuum light speed is the fastest physical speed---but it is finite as illustrated in the figure below (local link / general link: light_speed_earth_moon.html).
Recall again that "fastest physical speed" is a shorthand for fastest speed relative to a local inertial frame.
-
In 2011, there was a report
of faster-than-light neutrinos.
The measurements are the
OPERA neutrino anomaly---the
name comes from parent experiment, the
OPERA experiment.
These pesky faster-than-light neutrinos went away (i.e., proved to be an experimental error)---but if they had NOT, they would have marked a new revolution in physics.
- The Classical Limit:
The Galilean transformations and Newtonian physics are emergent theories (or approximate theories if that is your perspective) valid at low speeds, weak gravity, and in the macroscopic realm.
The limit of these conditions is the classical limit---which is tricky to define precisely, but you know what I mean.
The Galilean transformations and Newtonian physics are believed to be exactly true in classical limit---which is a good reason for calling them true emergent theories.
The more general transformations are Lorentz transformations---see the figure below (local link / general link: frame_transformations.html) for frame transformations redux.
But Newtonian physics had to be generalized to be correct in the framework of special relativity and the generalization included being changed to being inertial-frame invariant under the Lorentz transformations. The generalized mechanics is, of course, relativistic mechanics.
In the classical limit, Newtonian physics emerges from relativistic mechanics.
- Spacetime:
Because special relativity shows that time and space are connected, we use the term spacetime when we want to discuss these 4 dimensions of reality at the same time.
Spacetime is a standard term in Relativityspeak.
By the way, the time and space dimensions are distinct in special relativity and general relativity---just connected.
- World Line and Light Cone:
The concepts of world line and light cone in spacetime are illustrated in the figure below (local link / general link: spacetime_light_cone.html).
- FitzGerald Contraction:
Length is frame-dependent.
The length of a moving object is shorter along the direction of motion than the length observed in a frame which moves with the object.
This effect is called the FitzGerald contraction.
The effect grows as the relative velocity grows. The length observed in the object's (rest) frame is called the proper length.
The FitzGerald contraction formula is
L(v)=L_0*sqrt(1-v**2/c**2) , where v is the observer's velocity relative an object, L(v) is the observer's observed length for the object along the direction of motion, and L_0 is the length along the direction of motion measured in rest frame of the object. L_0 is called the proper length in Relativityspeak.The FitzGerald contraction is an observational effect---it is NOT a contraction due to forces---but it is NOT an illusion.
After all, observed velocity depends on the motion of the observer and that is NOT an illusion.
What we mean by velocity means that velocity does change between moving reference frames.
Similarly, what we mean by length means that length does change between moving reference frames.
Both cases of frame-dependence are considered to be kinematical effects or, one could say, spacetime effects.
To explicate the FitzGerald contraction further consider the question "What do we mean by length?" Answer: A length is a spatial separation measurable at one instant in time.
So if simultaneity is reference frame dependent, so is length.
Let's illustrate by a considering a paradox.
There are are two observers in relatively moving frames each with his/her own meter stick at rest in his/her frame.
Say Observer A sees Observer B measure A's meter stick. B gets less than 1 meter for A's stick.
Observer A saw B's measurements of the ends of A's stick and agrees that B would get less than 1 meter for the difference in position, but in A's frame those measurements did NOT happen simultaneously.
And a length measurement is one where the ends of an object are located SIMULTANEOUSLY.
So A would say that B did NOT measure the length of A's stick as far as A's frame is concerned.
In B's frame, B's measurements were SIMULTANEOUS.
In special relativity, time flow is frame dependent, and therefore so is simultaneity (as discussed in the light cone figure above), and therefore so is length.
The same situation applies if A measures B's stick. A gets less than 1 meter for a measurement that is SIMULTANEOUS in his/her frame, but NOT in B's frame.
The paradox is resolved---sort of.
A full explanation is beyond our scope, but some understanding is gleaned.
For another example, consider the pole vaulter in the figure below (local link / general link: pole_vault_fitzgerald_contraction.html).
- Time Dilation:
Time dilation and why "Moving clocks run slow." are explicated in the figure below (local link / general link: time_dilation_moving_clocks.html).
- The Twins Paradox:
The twins paradox is one of the weirdnesses of special relativity that follows from time dilation.
Take a pair of twins. They are initially a rest with respect to each other. One stays on Earth and the other goes on a rocket trip at a relativistic speed and then returns and the twins are again at rest with respect to each other. See the illustration of the twins in the figure below local link / general link: time_dilation_twin_paradox.html).
When back together again, both twins observe that the tripping twin's clocks have run slow compared to the stay-at-home twin and he/she is less aged than the stay-at-home twin.
-
Question: In the rocket trip case,
there is a definite asymmetry in the
time intervals for the twins which is the
twins paradox itself, but
how can this be if all motion is relative?
- Special relativity is wrong.
- Actually, NOT all motion is completely relative. Accelerated and unaccelerated motions relative to inertial frames are NOT the same. The tripping twin had to have been accelerated relative inertial frames---at least when he/she started, turned around, and stopped. Thus, his/her motion was physically distinct from the stay-at-home twin.
Answer 2 is right.Special relativity, like Newtonian physics, does distinguish unaccelerated and accelerated motions relative to inertial frames.
A full explication is beyond our scope.
- E=mc**2:
The mass-energy equivalence formula E=mc**2 falls rather naturally out of the physicsy derivation of special relativity.
It actually means two things as explicated in the figure below (local link / general link: e_mc2.html).
- Relativistic Mechanics:
Now special relativity can, of course, deal with forces and accelerations using relativistic mechanics (e.g., Law-44) which we mentioned in subsection The Classical Limit, but Einstein for various reasons was unsatisfied with how gravity and accelerations under gravity were treated in special relativity, and so went on to develop a relativistic theory of gravity: i.e., general relativity (GR). We discuss general relativity in section General Relativity below.
- The Vacuum Light Speed:
- Relativity Videos:
See also Relativity videos below (local link / general link: relativity_videos.html):
- The Relativity Postulate:
Certain aspects of special relativity had already discussed for some years by various people (e.g., George Francis FitzGerald (1851--1901), Hendrik Lorentz (1853--1928), and Henri Poincare (1854--1912)), but everything was very misty-cloudy before Einstein's work. The earlier researchers did NOT put all the pieces together.
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 22 problems 5--12 on atomic nuclei and E=mc**2.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 22.
- General Relativity
-
General relativity (presented 1915)
was a generalization of
special relativity
that Einstein
developed to give a more satisfactory treatment of
gravity
and accelerations under
gravity
than provided by
Newtonian gravity
(i.e., Newton's law of universal gravitation)
used in
relativistic mechanics
as given by special relativity.
- Newtonian gravity
as usually
conceived before Einstein
had its effects transmitted instantly.
If you moved an object, its
gravitational field
(which is the cause of the gravitational force) moves
instantly no matter how from the source object.
This violated Einstein's result
that the
vacuum light speed c = 2.99792458*10**8 m/s ≅ 3*10**8 m/s
= 3*10**5 km/s ≅ 1 ft/ns
was the highest physical speed
(i.e., highest speed relative to a local
inertial frame).
So Einstein had to
believe there was something incorrect about
Newtonian gravity
and relativistic mechanics
as given by special relativity.
- Another reason was that the
gravitational field
has an associated
gravitational potential energy
as it is ordinarily treated in
Newtonian physics.
But if the
gravitational field
has its own energy then
by special relativity
(via E=mc**2),
it has mass, and therefore should exert its own
gravitational field
that then should exert another
gravitational field
which should exert yet another
gravitational field,
and so on
ad infinitum.
This ad infinitum effect
does NOT appear in pure
Newtonian physics
where there is NO
E=mc**2,
but it is unavoidable in
relativistic mechanics
as given by special relativity
with a gravitational field
with
gravitational potential energy.
But though unavoidable, the
ad infinitum effect
also seems impossibly complicated.
General relativity
eliminates the
ad infinitum effect
by making the
gravitational field
NOT an ordinary
force field
(as for, e.g.,
electromagnetic force),
but a manifestation of the
curvature of 3-dimensional space
in such a way that it does NOT self-gravitate.
In general relativity,
there is NO
gravitational potential energy
or any other kind of
gravitational field energy
in an ordinary sense to have its own
gravitational field.
However, in general relativity, there is a non-local gravitational field energy embedded in the curvature of space. For more explication of non-local gravitational field energy, see Relativity file: e_mc2.html: Non-Local Gravitational Field Energy.
- There were other puzzles with
Newtonian gravity,
of course, that led
Einstein on.
- What Does General Relativity Consist of?
After the long excursion into tensors, tensor calculus, and differential geometry, Einstein eventually touched down in 1915 general relativity (see Wikipedia: History of general relativity) which is a complete theory of gravitation and motion under gravitation.
General relativity consists of two main parts: the Einstein field equations which replace Newtonian gravity (i.e., Newton's law of universal gravitation) and the geodesic equation which replaces Newton's 2nd law of motion (AKA F=ma), but only for gravity---for other forces, there is the relativistic mechanics 2nd law.
To explicate in a shorthand how the two parts interact, there is a mnemonic: the Mass-Curve-Motion Mnemonic:
- EOF
- The Einstein Field Equations Explicated:
The Einstein field equations in general relativity are the replacement for Newtonian gravity (i.e., Newton's law of universal gravitation) in Newtonian physics (which dictates the gravitational field of Newtonian physics).
For the original form and cosmological constant form of the Einstein field equations, see the figure below (local link / general link: general_relativity_field_equations.html).
see the figure below (local link / general link: physical_law_solution.html).- The Geodesic Equation Explicated:
The second main part of general relativity is the geodesic equation which is the GR replacement for Newton's 2nd law of motion (AKA F=ma) but only for the case where the force being replaced is gravity.
-
As aforementioned, for other
forces,
the replacement is the
relativistic mechanics 2nd law.
The fact that the replacement for
gravity is different than
for other forces shows that
gravity is NOT
force in the same sense
as other forces.
It is a manifestation of the
curvature of space.
But it sure acts like the other
forces in the
classical limit:
i.e., asymptotic limit of
well above quantum mechanics size scale,
small relative velocities
compared to the
vacuum light speed c = 2.99792458*10**8 m/s
(exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns,
and small curvature of
curved space
(which means in the weak
gravitational field limit).
In general, they stationary paths in whatever mathematical space you are considering.
In general general relativity, they are stationary paths in spacetime.
A stationary path is path through a space where between any 2 infinitesimally close points it is the shortest path.
A stationary path is NOT necessarily the shortest path between 2 points a finite distance apart.
To explicate by examples:
- In Euclidean space (flat space), a
geodesic
is a straight line which
is, in fact, the always the shortest path between any
2 points
no matter how far apart.
- Outer space
is asymptotically
3-dimensional
Euclidean space (flat space)
in the weak
gravitational field.
So in that limit, the
shortest distance between any
2 points
is a straight line.
- On the surface of a sphere
which is 2-dimensional
curved space
(i.e., 2-spherical space),
a geodesic is a
great circle
which is any circle which cuts
the sphere in
half.
A small circle
is a circle which does NOT cut
the sphere in
half.
Now a great circle
is always the shortest path
between any
2 points
less than or equal to half
a circumference apart if
you go in the right direction between the
2 points.
If you go in the wrong direction, the
great circle is still a
geodesic, but it is NOT
the shortest path between them evidently.
We illustrate an everyday life use of great circles in the figure below (local link / general link: great_circle_path.html).
- The Geodesic Equation Explicated:
- The Two Parts of General Relativity in Solving Systems:
If you are just given a fixed energy-momentum tensor T_ij for a system, then you can solve analytically in some few cases and numerically in any case with enough computer power for the geometry of spacetime from the Einstein field equations.
Then the geodesic equation can be used to find the motion of any test particle in the system. In a few cases, analytically and in any case numerically.
Note, a test particle is an object of sufficiently small mass-energy (or more exactly small mass-energy and momentum) that it does NOT perturb the system.
However, if the system does NOT have a fixed energy-momentum tensor T_ij (i.e., it consists of parts that can move), then one needs a simultaneous self-consistent solution: i.e., one where one solves the Einstein field equations and the geodesic equations for all the parts consistently with each other.
There is a difficult circularity in solving such systems with general relativity.
-
The situation is mnemonicked
by saying "In general relativity,
mass-energy
tells space how to curve and
curved space tells
mass-energy how to move."
Because of the circularity, getting a self-consistent solution is hard in general relativity.
-
In Newtonian physics,
the simultaneous self-consistent solution requires using
the Newton's law of universal gravitation
for gravity and
Newton's 2nd law of motion
(AKA F=ma).
So Newtonian physics also has circularity, but it is not as hard as in general relativity usually and in some cases rather easy.
Rest of this Subsection UNDER RECONSTRUCTION
Now as mentioned above, the curvature of space tells mass-energy how to move under gravity. More exactly, curvature is how gravity manifests itself in general relativity.
Now in the weak gravity limit, the effect of curvature reduces to the gravitational field of Newtonian physics.
And the gravitational structure of spacetime gives the gravitational force on mass-energy, and thus tells mass-energy how to move when no other forces act.
-
When other forces are acting,
gravitational structure of
spacetime
only partially tells mass-energy
how to move, of course.
- Solutions for Systems in General Relativity:
As discussed above in subsection The Two Parts of General Relativity in Solving Systems, problems in general relativity are rather CIRCULAR: Recall mnemonic: the Mass-Curve-Motion Mnemonic:
- EOF
Systems with exact analytic solutions in general relativity (i.e., solutions that can be written down in formulae) are very rare. For further explication of exact analytic solutions in general relativity, see the figure below (local link / general link: general_relativity_exact_solutions.html).
Grinding out numerical solutions is the essential method for solving general relativity for any system which is at all complex.
-
Question: If
general relativity
is so hard to understand and use, why do we use it?
- We don't use it. Mathematicians just like to exercise their brains with it. For mathematicians, see the figure below (local link / general link: ramanujan_1919.html).
- We like pain.
- It gives physical predictions that are right where Newtonian physics gives wrong predictions.
That was an easy one. But you could make a case for all of the above.
- Salient Verified Predictions/Results of General Relativity:
In the early years after 1915, the evidence for the superiority of general relativity relative to Newtonian gravity was NOT all that strong, but over the decades since 1915, general relativity has passed ever more stringent tests---tests which Newtonian gravity fails.
So general relativity is now well established as our best available theory of gravity.
It's amazing actually that general relativity has been so successful given that Einstein winged it up with very little experimental guidance beyond well known results fully explained by Newtonian physics---except for the problem with the orbit of Mercury: see subsection The Perihelion Shift of Mercury below.
Let us just briefly review the most salient verified predictions/results of general relativity:
- General Relativity
and the Classical Limit:
General relativity asymptotically becomes ordinary Newtonian physics in the classical limit: i.e., the asymptotic limit of well above the quantum mechanics size scale, small relative velocities compared to the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns, and small curvature of curved space (which means in the weak gravitational field limit).
Also in the asymptotic limit of small relative velocities compared to the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns, general relativity becomes asymptotically special relativity.
That these asymptotic limits of general relativity were built into general relativity by Einstein from the beginning since Newtonian physics and special relativity work excellently well in their respective asymptotic realms.
In fact, Newtonian physics and special relativity are true emergent theories in their respective asymptotic realms in the way of thinking of yours truly.
- The Perihelion Shift of Mercury:
In the 19th century, there was a problem in understanding the orbit of Mercury.
This problem concerns the perihelion shift of Mercury and is explicated in the two figures below (local link / general link: mercury_perihelion_shift.html; local link / general link: apsidal_precession.html).
- Gravitational Lensing:
Gravity bends light beams.
The effect has become known as gravitational lensing.
It takes strong gravity to make a noticeable bending: e.g., the gravity near a star.
Gravitational lensing is NOT predicted by pure Newtonian physics although various extensions can make some predictions---NOT verified ones though.
The point to emphasize is that general relativity predicted gravitational lensing quantitatively and this was verified in 1919.
The figure below (local link / general link: gravity_light_bending.html) illustrates gravitational lensing for a light ray grazing the surface of the Sun.
For gravitational lensing by the Sun, the prediction originally could only be verified in the visible band during total solar eclipses.
The 1919 Solar Eclipse Expedition carried out an observation of stars near the Sun during a total solar eclipse and quantitatively VERIFIED the prediction of gravitational lensing (see the figure below: local link / general link: 1919_solar_eclipse_expedition.html).
The announcement of the verification in 1919 made Einstein world famous. Before his fame was mostly only among physicists.
Many galaxies and galaxy clusters act as sources for gravitational lensing (FK-600--601; CK-406--407,422--423; HI-432,450,451).
In gravitational lensing, light from distant objects is focused into BRIGHTENED IMAGES and/or ARCS (if the object is sufficiently point-like).
Gravitational lensing of a remote galaxy by a galaxy cluster and gravitational microlensing are illustrated in the figure below (local link / general link: gravitational_lensing.html).
Nowadays gravitational lensing is a very important tool in determining the masses of gravitational lensing galaxies and galaxy clusters and forlooking for star-size gravity sources (e.g., Massive Compact Halo Objects (MACHOs) which are discussed in IAL 27: The Milky Way). One sees the gravitational lensing and infers the mass of the lens.
Also, the brightening effect of gravitational lensing allows one to observe objects that are too remote to be seen otherwise. This effect is becoming an important tool in studying the evolution of the observable universe: i.e., in cosmology.
- Gravitational Time Dilation: Clocks Run Slow in Gravitational Wells:
More precisely, gravitational time dilation is the effect that the deeper in a gravitational well the slower clocks run (i.e., the slower time passes) relative to outside the gravitational well.
A gravitational well is any localized source of gravity: e.g., a planet, star, black hole, etc.
Gravitational time dilation has been experimentally verified with terrestrial clocks at different altitudes and, in fact, must be accounted for in order for the Global Positioning System (GPS) to work as accurately/precisely as it does (see Wikipedia: Gravitational time dilation: Experimental confirmation).
- Gravitational Redshift:
The gravitational redshift is explicated in the figure below (local link / general link: gravitational_redshift.html).
- Gravitational Waves:
General relativity predicts that there should be gravitational waves (AKA gravitational radiation) traveling at the vacuum light speed (in a vacuum) produced by accelerated mass-energy (except in certain cases: see Wikipedia: Gravitational wave: Sources) somewhat analogous to electromagnetic waves or radiation (see Wikipedia: Gravitational wave). The prediction is verified.
Verifications of gravitational waves:
- Direct Detection of Gravitatonal Waves:
Gravitational waves were first directly detected by LIGO 2015 Sep14. For an explication, see the figure below (local link / general link: black_hole_merger_video.html).
- Earlier Indirection Detection of Gravitational Waves:
Before the direct detection of gravitational waves from GW150914, there was strong indirect evidence for gravitational waves.
The binary pulsar PSR B1913+16, discovered in 1974 consisting of two neutron stars, one of them a pulsar, has slowly decaying orbit with the neutron stars spiraling inward toward each other (see Wikipedia: Binary pulsar PSR B1913+16).
Because the system does contain a pulsar very precise measurements can be made of the orbital decay.
The loss of energy (specifically gravitational potential energy) from the PSR B1913+16 agrees within very small error with the energy that should be radiated away in the form of gravitational waves. See the evidence for this energy loss in the figure below (local link / general link: binary_pulsar_psr_b1913_16.html).
- Direct Detection of Low Frequency Gravitatonal Waves:
Low frequency gravitational waves (frequency of order 30 nHz ≅ 1 cycle/year) were reported verified in 2023 to almost the conventional standard for decisive discovery. The decisive discovery to the conventional standard will probably come circa 2025 (see Wikipedia: Pulsar timing array Observations).
We will NOT discuss frequency gravitational waves further, but some information, see Relativity file: gravitational_waves_low_frequency.html
- Earlier Indirection Detection of Gravitational Waves:
- Expansion of the Universe:
General relativity along with certain assumptions (most notably the cosmological principle) predicted the expansion of the universe according to Hubble's law in the 1920s (see IAL 30: Cosmology: Who Discovered the Expansion of the Universe and Hubble's Law?) before this was discovered observationally in 1929 (see IAL 30: The Expansion of the Universe).
- Black Holes:
Black holes are a prediction of general relativity and, as we will see in the section Do Black Holes Exist?, there is strong evidence for their existence.
In the opinion of yours truly and others, the evidence is NOW sufficiently strong that one can just say black holes exist. However, there is the unspoken qualification that alternative explanations for the evidence from observed gravitational wave events and Event Horizon Telescope (EHT) may exist, but NONE seem plausible at the moment.
Almost all scientific verifications are subject to such qualifications and usually that just goes without saying.
- The Perihelion Shift of Mercury:
But, in fact, it is believed to emerge from a lower-in-the-hierarchy emergent theory.
This is because general relativity is NOT consistent with quantum mechanics which is an even better verified theory.
People do NOT expect general relativity to hold in the microscopic realm of quantum mechanics.
It is believed that there must be a quantum gravity theory that applies in microscopic and super-dense conditions and that has a limiting-case form that is or at least closely approximates general relativity in those realms where general relativity is well verified.
-
General relativity
would be an emergent theory
relative to the correct quantum gravity theory.
There are, in fact, many quantum gravity theories, but NONE are verified.
Besides the quantum mechanics problem with general relativity, it is possible that both general relativity and Newtonian gravity are wrong in the realm of very low accelerations: i.e., below 10**(-10) m/s**2.
The counter theory to the conventional gravity theories is called MOND. At present, MOND is a generally disfavored theory.
We discuss MOND briefly in IAL 28: Galaxies. See also file gravity_mond.html.
- General Relativity Videos:
To conclude this section, yours truly might elect to show one or more of the General relativity videos shown below (local link / general link: relativity_videos.html):
- The Einstein Field Equations Explicated:
Why was a more satisfactory treatment needed? Two main reasons and other reasons:
Einstein had to go on a long excursion into very difficult math: tensors, tensor calculus, and differential geometry. A bit of differential geometry is illustrated in the figure below (local link / general link: space_curved.html).
Tensors, tensor calculus, and differential geometry are awful, but we'll do them if you like---just kidding.
- EOF
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 22 problems 5--12 on atomic nuclei and E=mc**2.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 22.
- Geometry (Reading Only)
-
As we remarked above in the section
General Relativity in
general relativity,
mass-energy
determines the geometry of
spacetime
and the geometry of
spacetime
tells
mass-energy
how to move.
- Flat and Curved Spaces:
Flat space and curved space are discussed the figure below (local link / general link: space_curved.html).
- Mathematically Analyzing 3-Dimensioal Curved Spaces:
We have difficulty picturing 3-dimensional curved spaces, but they can be mathematically analyzed.
Consider a 4-dimensional sphere in 4-dimensional flat space. The general name for higher than 3-dimemsional "spheres" is hypersphere. We CANNOT picture a hypersphere easily, but its equation is
w**2 + x**2 + y**2 + z**2 = r**2 , where w, x, y, and z are the 4 coordinates and r is the radius.
The surface of this hypersphere is a 3-dimensional curved space: it is a finite, but unbounded 3-dimensional space.
-
Slightly confusingly, the
4-dimensional hypersphere
is called a 3-sphere
because its surface is 3-dimensional.
An ordinary sphere
is called a 2-sphere
because it has a 2-dimensional surface in the jargon
spheres of different
dimensionality.
The general name of such spheres
is n-sphere, where
the surfaces as n dimensions.
A given mass-energy distribution gives rise to some curved space. In the absence of any mass-energy, one has a 3-dimensional flat space and general relativity reduces to special relativity.
Since general relativity has been shown to be an accurate theory for many effects, we believe real space is curved in a complicated way due to the complicated mass-energy present in real space.
In most regions, the curvature is too small to notice---a microbe living on a beach ball thinks its space is flat---and over short distances it is correct.
The curved space of space is asymptotically flat space on small enough scales. It also seems to be asymptotically flat space on the cosmic scale as we discuss in IAL 30: Cosmology.
- Picturing Curved Spaces:
As aforesaid, we have difficulty picturing 3-dimensional curved spaces.
But do we really picture 3-dimensional Euclidean space (flat space). All we see is 2-dimensional flat space. This is what light coming to the human eye gives us. The 3-dimensional world is projected into our 2-dimensional images. Our experience/instinct/intuition tells us how to interpret the images we see, how they would look from different perspectives, how things are arranged in 3 dimensions and how to move around and manipulate things in the 3-dimensional world.
Maybe if we lived in a curved 3-dimensional space we would just get used to it similarly.
For example, we might notice the curved space of Earth's surface more easily if we were relatively bigger compared to the Earth, and thus like the Prince on his asteroid: see the figure below (local link / general link: little_prince.html).
In fact, because we live in a layer on the Earth's surface, we live in a world with 2 large dimensions and 1 thin one.
- EOF
- Visualizing Unusual Geometries:
Actually, there are many techniques helping to visualize unusual geometries. An example of these is illustrated in the figure below (local link / general link: tesseract.html).
- Mathematically Analyzing 3-Dimensioal Curved Spaces:
Another way of putting the second point is that the curvature of spacetime manifests itself as gravity.
In the limit of weak curvature (i.e., near flatness), Newtonian gravitation (i.e., Newton's law of universal gravitation with the ordinary gravitational force and gravitational field) are emergent manifestations of the curvature of spacetime.
We will NOT do a full exposition of what this means, but instead try to get a little insight into 4-dimensional Euclidean geometry, non-Euclidean geometry, geodesics, and GR geodesics
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 22 problems 5--12 on atomic nuclei and E=mc**2.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 22.
- History of the Idea of Black Holes
-
What is the history of black holes?
- Newtonian Black Holes:
In pure Newtonian physics, it is NOT absolutely clear how gravity affects light.
-
By saying "in pure
Newtonian physics"
we mean imagine that
Newtonian physics
was a fundamentally true theory in all limits, NOT
just the classical limit, and see what things that implies.
But on the other hand, Newton himself (see figure below (local link / general link: newton_principia.html) regarded light as made of particles---classical particles, NOT like modern photons---and this idea was current throughout the 18th century.
If so, then it was possible to imagine an object sufficiently massive and compact that light could NOT escape from its intense gravity in Newtonian physics.
-
Just to recapitulate on
escape velocity:
The equation for escape velocity in Newtonian physics is (without derivation)
v_escape = sqrt(2GM/r) , where G is the gravitational constant, M is the mass of a spherically symmetric gravity source that has radius =< r, and r is the radius from which the escaping test particle starts.The formula is only exact for test particle: i.e., objects of vanishingly small mass. However, if the object's mass is much less than M, formula is of high accuracy. The escape of the object is to infinity: the particle will NOT return. The direction of escape makes no difference provided only gravity acts: i.e., the test particle does NOT hit a planet or have to contend with an atmosphere.
For example the escape velocity from the Earth's surface is 11.2 km/s (see Wikipedia: List of Escape Velocities).
For more on escape velocity, see the figure below (local link / general link: newton_cannonball.html).
v_escape = sqrt{2GM/r} > c .For a classical particle (meaning one with some mass), there will be NO escape for the classical particle if it is moving at the vacuum light speed or less in Newtonian physics.
If we rearrange, the escape velocity formula, we get that for a spherically symmetric body of mass M compacted to a radius r ≤ R_sch=2GM/c**2, there will be NO escape even for a classical particle of light if it starts from radius less than or equal to r: i.e., from
r ≤ R_sch = 2GM/c**2 .
-
The case of r = R_sch is usually considered "no escape" for
light since
light would have zero energy when
it got infinitely far the start point.
A classical particle of
could have
zero kinetic energy.
But, from a modern perspective, we know light
of zero kinetic energy is nothing---well,
if it's NOT nothing, we don't know what it is.
-
From inside the event horizon,
nothing gets out even on a non-escape
trajectory.????
The "semi" is because the right quantities were going into the calculation, and so something like the right answer could be expected to emerge.
If you compact an object to within its Schwarzschild radius, it will have an event horizon and will be a black hole.
Having an event horizon is the defining characteristic of a black hole in whatever theory of gravity one uses.
Because light CANNOT escape from event horizon (and from within it, of course), black holes are very, very black: there is no light at all coming from within the event horizon.
- Newtonian Black Holes Are Called Dark Stars:
A Newtonian black hole is called a dark star. The term black hole was NOT in general use until about 1967---see below subsection Black Holes Gain Fame.
Dark stars (and maybe their name) were first thought of by John Michell (1724--1793) in 1783.
-
Note, it was known in 18th century
that the vacuum light speed
was finite and there was a value that was only ∼ 0.4 % larger than the
true value
(see Wikipedia: Speed of light:
History).
Pierre-Simon Laplace (1749--1827) (see figure below (local link / general link: pierre_simon_laplace.html) in 1796, apparently unaware of Michell's work, also considered dark stars.
Dark stars attracted little interest because even their existence as theoretical objects was NOT certain since one must treat light as obeying Newtonian physics which was an ad hoc hypothesis---and a wrong one too---and certainly NO real object seemed to correspond to them until the modern discovery of black hole candidates starting with Cygnus X-1 in 1971 (see Wikipedia: Cygnus X-1: Discovery and observation).
- The Schwarzschild Solution:
First note the explication of physical law and solutions below (local link / general link: physical_law_solution.html).
The Schwarzschild solution is very important because the behaviors of objects in the vicinity of spherically symmetric mass distributions is very important in astrophysics: e.g., planets around the Sun (ABS-194).
The Schwarzschild solution does NOT apply inside the spherically symmetric mass distributions: e.g., inside the Sun.
Schwarzschild noted that there was a special length scale in the Schwarzschild solution which we now call the Schwarzschild radius:
R_sch = 2GM/c**2 ,
which was first derived from Newtonian physics as noted above in subsection Newtonian Black Holes.Funny things would happen if a mass were compacted to within its Schwarzschild radius (i.e., within its event horizon as we now call it)---the object became what we now call a black hole.
Schwarzschild himself thought the black hole prediction of the Schwarzschild solution was physically meaningless.
- Black Holes Gain Fame:
J. Robert Oppenheimer (1904--1967) and Hartland Synder (1913--1962) in 1939 seem to be the first to seriously consider black holes (without using that term) and consider how a star-like object could collapse to one (ST-338).
There was NOT much interest in these new non-Newtonian black holes until the 1960s when the discovery of quasars and pulsars (which are radio-pulse emitting neutron stars) forced people to consider seriously the existence of exotic compact objects (ST-338).
The term black hole gained currency sometime in the 1960s. Who first coined it is NOT known.
The first recorded use of the term black hole occurred in a science news story by journalist Ann E. Ewing (1921--2010) in 1964: see figure below (local link / general link: ann_ewing.html).
- Black Holes Can Come Into Existence:
That black hole solutions of general relativity existed was known since J. Robert Oppenheimer (1904--1967) and Hartland Synder (1913--1962) if NOT before.
But that a solution exists does NOT prove that there are physical pathways to get to black holes from actual physical objects.
Proving that there were such physical pathways was done by Roger Penrose (1931--) in 1965. For more on Penrose and his proof, see the figure below (local link / general link: roger_penrose.html).
- A First Word on the Physics of Black Holes:
Black holes have been thought of as very simple objects until circa 2012.
There is a famous aphorism of John A. Wheeler (1911--2008): "black holes have no hair" which just means they are simple objects---in a certain sense---without a lot of features like hair, fingers, toes, etc.
The no-hair theorem itself: If one can ignore perturbations from other masses, then aside from its location in spacetime a black hole is fully specified by just three parameters: mass, angular momentum (a measure of rotation), and net electric charge.
In fact, the no-hair theorem even if NOT fundamentally true is probably a useful model of black holes for many purposes, but NOT those deep in the realm of fundamental physics.
We will NOT go deep in the realm of fundamental physics---except for a bit on Arcane Problems with Black Holes in the insert below (local link / general link: black_hole_arcane_problems.html).
- The Three Kinds of Ideal Black Holes:
There are three kinds of ideal black holes (i.e., ones where you can ignore perturbations and Arcane Problems with Black Holes: see Black Hole file: black_hole_arcane_problems.html):
-
Schwarzschild black holes:
These have zero angular momentum
(the key quantity of rotational motion) and zero net
electric charge.
The Schwarzschild black holes are the black hole that follow from the Schwarzschild solution.
Since most objects in the universe are rotating with respect to inertial frames, exact Schwarzschild black holes are unlikely to exist, but low-angular-momentum black holes probably approximate Schwarzschild black holes.
- Kerr black holes:
These have NON-ZERO angular momentum,
but zero net electric charge.
They are predicted to exist by the Kerr solution discovered by Roy Kerr (1934--): see the figure below (local link / general link: roy_kerr.html).
The Kerr black hole emerged as one of the results if the rotating mass was compacted to within the Kerr-Schwarzschild radius which is Kerr generalization of the Schwarzschild radius (ABS-265).
Kerr black holes are the most likely black holes to be realized in nature since almost all objects in space are rotating to some degree.
- Kerr-Newman black holes: These have NON-ZERO angular momentum and net electric charge (see Shapiro & Teukolsky 1983, p. 357).
Usually, macroscopic bodies in the universe are nearly neutral because any charge imbalance quickly attracts neutralizing charge.
Thus, black holes that show significant Kerr-Newman black hole behavior seemed unlikely to exist.
However, since circa 2015, it is hypothesized that Kerr-Newman black holes do exist and may have observable effects: e.g., as the sources of some fast radio bursts (FRBs) (see, e.g., Liu et al. 2016).
So there may be mechanisms to significantly charge black holes and keep them charged.
-
In fact, combined
electric fields and
magnetic fields
can maintain astrophysically important charge separations as
yours truly is informed by colleague Bing Zhang.
We should note that there are concerns that the Kerr-Newman black hole solution may NOT be a valid physical solution (see Wikipedia: Kerr-Newman metric: Some aspects of the solution). So some rethinking of the Kerr-Newman black hole solution may be needed.
We will NOT consider Kerr-Newman black holes further in IAL 25.
- Kerr-Newman black holes: These have NON-ZERO angular momentum and net electric charge (see Shapiro & Teukolsky 1983, p. 357).
- Newtonian Black Holes Are Called Dark Stars:
- Schwarzschild Black Holes
- Cartoons and Explication of Schwarzschild Black Holes:
Schwarzschild black holes (which recall have zero angular momentum and zero net electric charge) are explicated in the figure below (local link / general link: black_hole_schwarzschild_cartoon.html).
Their event horizon is a spherical surface with radius the Schwarzschild radius R_Sch=2GM/c**2.
Recall that because light CANNOT escape from event horizon, black holes are very, very black: there is no light at all coming from within the event horizon as the figure above (local link / general link: black_hole_schwarzschild_cartoon.html) and the figure below illustrate.
-
Actually, there probably can be escaping emissions from very near the
event horizon as
we will discuss below in section Hawking Radiation.

Caption: "Inside of the event horizon all paths bring the particle closer to the center of the Schwarzschild black holes. It is NO longer possible for the particle to escape."
Note, the plot horizontal axis is 1 dimension of space and note, the location of the Schwarzschild radius R_Sch=2GM/c**2.
The vertical axis is time.
The distortions of spacetime shown in the image by yellow curves are beyond current ability of yours truly's to elucidate.
Credit/Permission: © User:Vanessaezekowitz, User:Avsa / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia: File:BH-no-escape-3.svg.
- The Compression to a Black Hole:
If any object is compressed to within event horizon for its mass as set by its Schwarzschild radius, then the object according to general relativity must collapse to being black hole: e.g., the Sun compressed to with a 3-km-radius event horizon would become a black hole.
For reference, the Schwarzschild radius formulae are given below (local link / general link: black_hole_schwarzschild_radius_formulae.html):
- EOF
- An Artist's of a Stellar Mass Black Hole Seen Close Up:
An artist's conception of an isolated stellar mass black hole see close up is shown in the figure below (local link / general link: black_hole_isolated_up_close.html).
- The Singularity:
In Schwarzschild solution, there is NOTHING to stop the mass compressed to within its event horizon from collapsing to a point of infinite density: a gravitational singularity.
-
In mathematics, a point where a function goes to infinity is an example of
a mathematical singularity: e.g.,
1/x has a singularity at x = 0 .
No pressure force can stop the formation of a gravitational singularity once matter has been compressed to within the event horizon for that matter's mass.
The reason is that pressure itself has an associated mass-energy, and thus is gravitating (ST-335).
If pressure becomes too intense, its self-gravity actually exceeds its outward pushing force.
-
Question: Is the gravitational singularity real?
- Yes, it is a prediction of general relativity:
our best theory of gravity.
- Maybe.
- Probably NOT.
Whenever a physical theory gives an infinity, it usually means you have extrapolated it beyond its realm of validity.
In the case of general relativity, it is strongly believed it must fail when gravity becomes intense at the microscopic level (which is where the gravitational singularity as point must be) since general relativity is NOT a quantum gravity theory.
Answer 3 is probably right, but maybe an argument could be made for answer 2.Answer 1, I think, CANNOT be accepted: just because general relativity is our best theory of gravity does NOT prove it is right in all predictions.
But if there is no singularity, what is at the center of black holes?
Maybe some exotic compact form of matter, but we have no consensus idea of what that is.
- The Event Horizon:
The event horizon delimits a region that CANNOT communicate with the outside world.
Nothing from inside can get out.
-
Which reminds me of an old
Dave Allen (1936--2005) story about
two Irishpersons returning from a night at
the pub ...
The inside is disconnected from the rest of the universe.
The artist's misconception in the figure below (local link / general link: black_hole_artist_misconception.html) illustrates the disconnection.
- Into the Black Hole:
What happens to a test particle (i.e., a particle of vanishingly small mass-energy) approaching the event horizon?
-
Because it has vanishingly small
mass-energy,
the particle CANNOT perturb the
black hole.
By faraway clocks, it takes the particle infinite time to reach the event horizon.
The test particle by its own clock does pass through the event horizon in a finite time.
Remember in general relativity time slows down in a gravitational well from an OUTSIDE perspective.
-
Question:
Even though test particle
never gets in from an outside perspective,
the faraway observer must lose track the test particle eventually.
Why is this?
- Light signals from the
test particle
gravitationally redshift
and lose energy coming out of the
gravitational well
of the
black hole.
Recall photon energy is given by E = h*c/λ (see Wikipedia: Matter waves: de Broglie relations), and thus photons lose energy as wavelength λ increases (i.e., redshifts).
The signals from the infalling particle must get progressively weaker as it falls deeper into the gravitational well of the black hole.
In fact, the gravitationally redshift goes to infinity as the particle approaches the event horizon (i.e., λ→∞ as r→R_sch=(2GM/c**2) the Schwarzschild radius or R_event_horizon_general). See Wikipedia: Gravitational redshift: Exact solutions.
Thus, detector of finite sensitivity must eventually lose track of the test particle.
- No known reason.
Answer 1 is right.Easy question, eh?
-
Question: Does the fact that a
test particle never gets into the
event horizon
from an outside perspective
mean that black holes can never grow from an outside perspective?
- Yes, that is what it means.
- No. A test particle has vanishingly small
mass-energy,
and so
does NOT perturb the spherically-symmetric
Schwarzschild solution
at all.
Any particle of NON-ZERO mass-energy must perturb the Schwarzschild solution to some degree.
Somebody's analysis shows that infalling mass-energy does get into the event horizon eventually and that makes the black hole mass, and thus event horizon of a black hole grow.
Answer 2 is right.It's actually very hard to get a reference to spit out this factoid.
So I had to appeal to an actual expert person.
And she assured me that real matter with finite mass-energy gets into black holes and black holes and event horizon event horizons do grow.
But she didn't tell how long it takes for mass-energy to fall in. Maybe we don't want to know.
The somebody who gave the analysis may have been Roger Penrose (1931--) himself.
- Ripped Apart:
What happens to a finite-sized object as it falls toward a black hole?
The difference in gravity between the closer and farther parts of the object will eventually tear the object apart.
The differential gravity effect is common in many contexts and is called the tidal force---because it is the cause of the tides.
The tidal force will even tear the atoms apart some point (FK-547--548). But can it tear elementary particles apart? The answer probably requires having an established quantum gravity theory---which do NOT have. The elementary particles are shown in the blue of the figure below (local link / general link: particle.html).
The ripping apart is humorously referred to as spaghettification.
Nowadays there is a lot of interest in stars being ripped apart as they inspiral around supermassive black holes (see section Supermassive Black Holes).
These events are called tidal disruption events (TDEs) and are highly luminous because when the debris from the TDE hits the accretion disk (orbiting the supermassive black hole) turning kinetic energy into heat energy some which becomes emitted electromagnetic radiation (EMR)????.
More viscerally, when the ____ hits the ___ ...
TDEs are interesting intrinsically as a case of transient astronomical events and for providing information about the environment of supermassive black holes.
- Birkhoff's Theorem:
There is a theorem, called the shell theorem, in Newtonian physics (proven by Newton himself) that gravitation at any point outside a spherically-symmetric mass distribution depends only on the mass interior to that point, and NOT on the mass distribution itself as long as it is spherically-symmetric.
-
That two spherically-symmetric masses
interact like point masses is a
corollary of the shell theorem.
It illustrated in the figure below
(local link /
general link: gravity_two_spheres_animation.html).
What does this mean?
Say you were at a distance equal to the radius of the Sun from the center of spherically-symmetric object that was entirely interior to your location.
The gravitation you would feel would be the same no matter how compact the object was: it could be that the object was as big as the Sun or as compact as a black hole.
The upshot is that the powerful gravity and exotic effects of a black hole only occur when you are relatively close to its event horizon.
-
Question: If the
Sun suddenly and
without any other effect turned into a
black hole,
what would happen to the motion of the planets?
- Nothing.
- The planets would escape from the solar system.
- The planets would fall into the solar
black hole
because of its irresistable gravity.
Answer 1 is right.- Spacetime Around a Black Hole:
The geometry of spacetime around a Schwarzschild black hole is an extreme case of the geometry of spacetime around any spherically symmetric mass distribution.
This geometry follows from the the Schwarzschild solution (1916) to general relativity (1915). We explicate the geometry in the figure below (local link / general link: schwarzchild_solution_spacetime.html).
We discuss such events below in subsubsection Via Gravitational Microlensing Events.
One could go on and on about Schwarzschild black holes, but that's enough.
- The Compression to a Black Hole:
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 25 problems 2--7 on black holes, Schwarzschild solution, Kerr solution, event horizon, and the gravitational singularity.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 25.
- Kerr Black Holes
-
Recall Kerr black holes
have NON-ZERO angular momentum,
but zero net electric charge.
Kerr black holes are explicated the figure below (local link / general link: black_hole_kerr.html).
- Do Black Holes Exist?
-
Do unicorns exist?
See the figure below
(local link /
general link: unicorn_virgin.html).
- There are super compact massive objects of a few to a few tens of
solar masses
(stellar mass black holes)
and others in the range 10**5 to 20*10**9 M_☉
(supermassive black holes).
These objects are NOT neutron stars
or anything else less exotic than neutron stars.
In modern astronomy, these super compact objects fill roles as stellar-mass X-ray sources and the engines of active galactic nuclei.
- Black holes
are a prediction of general relativity
which has been verified in many respects.
This prediction includes the event horizon (the point of NO return) and this is the absolute defining feature of black holes.
However, the black hole singularity prediction of general relativity is NOT believed. But this is because we strongly believe quantum gravity must prevent collapse to a point mass. Quantum mechanics is an even better verified theory than general relativity.
- Direct observations of the
gravitational wave events
and ostensible black hole shadows
are super-strong evidence for
black holes.
- There are NO compelling alternative
theories at present.
And if there were, they would probably be of very exotic objects too.
- Super Massive Compact Objects Exist:
There are super compact massive objects of a few to a few tens of solar masses (stellar mass black holes) and others in the range 10**5 to 20*10**9 M_☉ (supermassive black holes). These objects are NOT neutron stars or anything else less exotic than neutron stars.
In modern astronomy, these super compact objects fill roles as stellar-mass X-ray sources and the engines of active galactic nuclei.
The super compact objects are conventionally called black holes.
So black holes exist in a conventional sense.
-
If black holes did NOT exist,
we would have to invent them since they are so useful in explaining (or explaining away)
some X-ray sources
and all active galactic nuclei (AGNs).
The event horizon is the absolute defining characteristic of black holes.
- Prediction of General Relativity:
Black holes are a prediction of general relativity. So they exist within the theoretical world of general relativity necessarily.
If general relativity is wrong about reality, black holes may NOT exist in reality.
But they still may exist anyway. The defining absolute characteristic of black holes is really the event horizon. If it exists, black holes exist.
But if general relativity is SUFFICIENTLY right black holes exist.
Why just SUFFICIENTLY right?
We know general relativity is very probably NOT exactly correct in the microscopic limit because it is NOT consistent with quantum mechanics.
We believe that the exactly correct theory of gravity in the microscopic limit will be a quantum gravity theory. General relativity, if it is exactly correct in the macroscopic limit, would be macroscopic limit of the correct quantum gravity theory.
Alas we have NO established quantum gravity theory yet.
One aspect of black holes predicted by general relativity that we do NOT believe is the black hole singularity---see the figure below (local link / general link: black_hole_schwarzschild_cartoon.html).
-
The formula for the Planck density is
ρ_Planck = c**5/(ħ*G**2) = 5.15500*10**96 kg/m**3 , where c is the vacuum light speed, G is the gravitational constant, and ħ (h with a stroke through it pronounced h-bar) is the Planck constant divided by 2π (CL-123).
So the prediction of mass-energy being compacted to a singularity of infinite density (see figure above: local link / general link: black_hole_schwarzschild_cartoon.html) is widely thought to be probably wrong.
We think some exotic quantum state of matter must exist in the deep interior of the event horizon, but without an established quantum gravity theory we do NOT have any established idea of what that is.
However, though NOT a quantum gravity theory, general relativity seems to be a correct emergent theory from quantum gravity in that is passes all observational tests sofar.
However, there are also the possible modifications to general relativity and Newtonian gravitation demanded by MOND (see section General Relativity above and file gravity_mond.html).
These modifications are NOT necessarily quantum gravity per se.
The majority of experts think MOND is NOT correct and who knows what implications it would have for black holes if it were correct.
- The Super-Strong Evidence for Black Holes:
It is as follows:
- The Gravitational Wave Test
for Black Holes:
The observation of gravitational wave events from black hole mergers (starting with the first observation of gravitational waves, AKA GW0150914) is a confirmation that gravitational waves exist, but it is also a confirmation of black hole physics since the gravitational wave events from black hole mergers match the predictions for inspiraling and coalescing stellar mass black holes
To be more specfic, they match predictions based on their macroscopic properties which include the general defining property of black holes the event horizon---that surface from which nothing, NOT even light can escape.
-
Note, as aforesaid,
if general relativity is
wrong about reality,
black holes
would still exist if
the event horizon existed
since that is general defining property of
black holes.
However, one can always say that some theoretical exotic astronomical objects other than black holes could generate the observed gravitational wave events.
True, but there are NO plausible theoretical exotic astronomical objects that could do so.
One can never be absolutely sure that there none, but quibbling that they might exist seems pointless now without more evidence.
Note, it is generally true in science that we accept a theory as true once it has passed enough hard tests---with it just being understood that what we mean is that it is adequate to all the evidence and we do NOT foresee it being falsified by new evidence.
The gravitational wave events have put black holes into that category in the opinion of most experts---probably NOT all---there are always quibblers---or as Charles Darwin (1809--1882) would say wrigglers (see Eiseley 1961, p. 115, 295; Loren Eiseley (1907--1977))---Darwin was fond of worms: see Wikipedia: Darwin from Insectivorous Plants to Worms.
- Direct Observation of a Black Hole Shadows:
The Event Horizon Telescope (EHT) announced 2019 Apr10 the imaging of the supermassive black hole (SMBH) which is near the center of mass of M87 (see Wikipedia: M87: Supermassive black hole), the giant elliptical galaxy near the center of the Virgo Cluster.
To be more precise, the EHT imaged the SMBH's black hole shadow and surroundings.
The figure below (local link / general link: m87_virgo.html) explicates how the EHT image verifies almost certainly the existence of the event horizon, and so the existence of black holes.
Note, this verification is somewhat independent of the validity of general relativity. As aforesaid, if the event horizon exists---that surface from which nothing, NOT even light, can escape---then black holes exist whether general relativity is true or NOT.
- More Evidence from the Milky Way and Sgr A*:
The EHT has reported that they have imaged the event horizon of Sgr A*, the supermassive black hole at (or, to be more precise, nearly at) the Milky Way center (AKA Galactic center of mass) (see Wikipedia: Sagittarius A*).
The EHT imaging is discussed in the figure below (local link / general link: sagittarius_a_star.html).
- More Evidence for Black Holes:
Beyond the current evidence for black holes, more indirect evidence can be found.
One must remember that are our understanding of black holes is currently plagued by the Arcane Problems with Black Holes that we briefly discuss in the insert above (local link / general link: black_hole_arcane_problems.html).
- Direct Observation of a Black Hole Shadows:
- No Compelling Alternative Theories to Black Holes:
Circa the 2020s, there are NO compelling alternative theories to black holes.
However, there less-than-compelling ones that have been discussed:
- In the first one, super compaction leads NOT to a
black hole, but
to a perhaps equally weird object, a
gravastar
(see, e.g.,
Mazur, P. O., & Mottal, E. 2001,
Gravitational Condensate Stars: an Alternative to Black
Holes, gr-qc/0109035).
- In the second one, super compaction leads NOT to a
black hole, but
to another perhaps equally weird object, a
black star.
- Yes with a Qualification Usually Unspoken:
Yes with a qualification usually unspoken because since 2015 strong evidence for black holes (i.e., objects conforming to the black holes of general relativity) has appeared.
So strong that most people now would just say black holes exist.
The usually unspoken qualification is that maybe there is some other way of explaining the evidence without black holes. But that explanation would be astonishing.
There is nothing unusual about the qualification. Most well established theories have the same qualification. It is just understood that there is that qualification which is too tedious to mention most of the time.
- Prediction of General Relativity:
Yes:
But this is subject to the qualification (usually left as understood) that maybe there is an alternative theory that is just as good or better than black holes for the evidence that we have. However, such an alternative theory would be astonishing.
In fact, many very well established theories are subject to the same unspoken understood qualification.
We will expand on all points above, in the subsections below:
- How Do Black Holes Come into Existence?
-
Given that
black holes
exist, another question is how could they actually come into existence.
-
Stellar Mass Black Holes from Core Collapse Supernovae:
The main channel for making stellar mass black holes is thought to be the more massive core collapse supernovae. Recall we discussed core collapse supernovae in IAL 23: Late Star Evolution and Star Death.
For core collapse supernovae with progenitors of initial stellar mass (i.e., initial main-sequence star mass) of over ∼ 20 M_☉ (see Wikipedia: Black hole: Gravitational collapse), the core collapse does NOT stop at a neutron star, but continues to a black hole.
Note, the critical initial stellar mass of 20 M_☉ is very uncertain. We understand core collapse supernovae qualitatively reasonably well, but quantitative understanding is still weak. Also, inital stellar mass may NOT be the only parameter determining whether core collapse supernovae yield black holes or neutron stars.
Stellar mass black holes from core collapse supernovae probably have masses in the range from the maximum neutron star mass ∼ 2.2 M_☉ to a ∼ 60 M_☉ (see Wikipedia: Stellar black hole: Upper mass gap) The gravitational wave event GW190521 (2019may21) caused by black hole merger had a primary black hole with mass 85(+21/-14) M_☉ (see Wikipedia: GW190521: Physical significance) which exceeds the ∼ 60 M_☉, and so maybe that limit needs revision.
- Stellar Mass Black Holes from Compact Star Mergers:
Compact stars (AKA compact remnants) are white dwarfs, neutron stars (see figure below (local link / general link: neutron_star_cutaway.html), and black holes (here meaning stellar mass black holes).
If you a compact binary (i.e., a binary system of compact stars), then loss of energy due to gravitational waves will over long periods of time (typically megayears to gigayears) will cause them to inspiral and merge. If the total mass is greater than the maximum neutron star mass ∼ 2.2 M_☉, then merge compact star will become a black hole.
This channel of black hole formation goes on all the time at some rate for all the various combinations of compact binary stars. However, white dwarf-white dwarfs mergers to form black holes are probably very rare and a negligible channel since two white dwarfs in a compact binary probably very rarely have total mass is greater than the maximum neutron star mass ∼ 2.2 M_☉.
For gravitational wave event detections, black hole mergers, neutron star mergers, and neutron star-black hole mergers are probably most common.
Mergers with at least one compact star being a black hole do NOT, of course, create a new black hole, just make a larger black hole.
The range of black hole masses created by this process range from the maximum neutron star mass ∼ 2.2 M_☉ to over 100 M_☉.
The gravitational wave event GW190521 (2019may21) caused by black hole merger gave new coalesced black hole of mass 142(+28/-16) M_☉ (see Wikipedia: GW190521: Physical significance). Circa 2020, 142(+28/-16) M_☉ seems to be the record mass for stellar mass black hole.

Caption: "Two-dimensional representation of gravitational waves generated by two neutron stars orbiting each other."
The caption isn't really adequate to explain this animation, but it's pretty to look at.
It imagine the ripples represent expansions and contractions of space which would expand and contract objects in space that they passed through---but no one's telling.
Credit/Permission: NASA, circa or before 2005 / Public domain.
Image link: Wikipedia: File:Wavy.gif.
- The Formation of Intermediate-Mass Black Holes:
Intermediate-mass black holes (masses of order 100 to 10**5 M_☉) are between the two cases of stellar mass black holes and supermassive black holes.
Only a few intermediate-mass black hole candidates are known (see Wikipedia: List of intermediate-mass black hole candidates).
However, there is NO certain detection yet it seems (see Wikipedia: Intermediate-mass black holes), except gravitational wave event GW190521 (2019may21) gave rise to an intermediate-mass black hole of 142(+28/-16) M_☉ (see Wikipedia: GW190521: Physical significance; Wikipedia: Intermediate-mass black hole: Observational evidence). Note, GW190521 (2019may21) intermediate-mass black hole is a small one and is only one by the precise lower limit definition of 100 M_☉ which is a bit arbitrary and it formed from a merger of stellar mass black holes. So it is marginal intermediate-mass black hole and perhaps rare kind of intermediate-mass black hole.
There is one probable intermediate-mass black hole (which is NOT just marginally a intermediate-mass black hole) according to evidence as of 2024. This probable intermediate-mass black hole is the Omega Centauri black hole candidate (mass ⪆ 8200 M_☉) which is near the center of Milky Way globular cluster Omega Centauri (see Daryl Haggard & Adrienne Cool, 2024 Jul10, Nature, "Speedy stars blow the cover of hidden black hole"; Wikipedia: Omega Centauri; Evidence of a central black hole). Evidence for/against the Omega Centauri black hole candidate (mass ⪆ 8200 M_☉) will probably take some years after 2024 to emerge.
Perhaps there are NO intermediate-mass black holes (other than small ones like GW190521 (2019may21)) since there is NO process to create them. Or they may be rare because their formation process is rare. On the other hand, they may be abundant, but just hard to detect.
If they exist, their formation process (or processes) may be the same as for the supermassive black holes. We discuss the possible processes for the formation of supermassive black holes below in subsection The Formation of Supermassive Black Holes.
We will NOT consider intermediate-mass black holes further in IAL 25.
- The Formation of Supermassive Black Holes:
Supermassive black holes have mass ≥ 10**5 M_☉ and typically have masses of millions to billions of solar masses. These are the ones that the Event Horizon Telescope (EHT) is directly imaging---one so far and maybe one more soon.
Where do they come from?
During the formation of galaxies, it is believed that supermassive black holes form in the galaxy centers.
Recall the "center" is probably the galaxy center of mass or nearly, but no reference seems to spit out this factoid.
In fact, the current hypothesis is that nearly all large galaxies have supermassive black hole near their centers (see Wikipedia: Supermassive black holes). Evidence for this has been growing since the 1970s.
There are several theories about the formation of the initial supermassive black holes (see Wikipedia: Supermassive black hole: Formation). We will just describe two:
- The favored current theory
of formation is that super-massive
Population III stars
provided the initial
supermassive black holes at the
center of the dark matter
gravitational wells
which formed the initial galaxies.
Recall the Population III stars were the first stars formed after the Big Bang. They became super-massive because they had nearly zero metallicity, and so exploded as super supernovae very rapidly, polluting the interstellar medium (ISM) with metals which prevented the formation of further super-massive stars.
- Another popular theory
is that the first
supermassive black holes
were primordial black holes.
See subsection Primordial Black Holes below.
Whatever their origin, the initial supermassive black holes grew larger through disk accretion and mergers with other supermassive black holes: i.e., supermassive black hole mergers. The supermassive black hole mergers followed galaxy mergers. When two galaxies merge, their respective central supermassive black holes eventually sink to the center of the new merged galaxy due to dynamical friction. However, when the pair of supermassive black holes get within a few parsecs of each other dynamical friction is expected to become ineffective at getting them closer and orbital energy loss due to gravitational waves is ineffective on the time scale of the age of the observable universe = 13.797(23) Gyr (Planck 2018) until they are separated by ∼ 0.001--0.01 pc. But supermassive black holes do seem to have merged. So theoretically explaining how the pair of supermassive black holes actually merge is the final parsec problem for which there are several theories (see Wikipedia: Binary black holes: Final parsec problem).
- Primordial Black Holes:
It has been hypothesized that primordial black holes may have been formed by density fluctuations in an early phase of the Big Bang.
Their hypthetical mass range is 10**(-8) kg to 1000s of solar masses.
One idea is that the black holes of black hole mergers that give rise to gravitational wave events or some of them anyway may be such primordial black holes since their formation by other means has been questioned.
We must emphasize that primordial black holes are an extra hypothesis of Big Bang theory.
We CANNOT predict if they exist or NOT with any certainty.
But they may be the solution to the question what is dark matter.
Maybe dark matter is NOT an exotic particle (which has long been the favored theory) and is primordial black holes.
This idea would explain why all attempts to find exotic dark matter particle in the laboratory have failed so far: it doesn't exist.
Another idea is that small primordial black holes with masses from about 10**(-8) kg to Earth mass M_⊕ = 5.9722(6)*10**24 kg could have been formed in the Big Bang.
Such small primordial black holes were introduced as a rth of the WebThe birth of the Webhypothesis by Stephen Hawking (1942--2018) in the early 1970s (FK-543--544). There is no evidence yet that small primordial black holes exist, but they are an interesting possibility because they could be detectable proving both that primordial black holes and that Hawking radiation exists.
We will discuss small primordial black holes again in the section Hawking Radiation.
There could also have been very massive primordial black holes.
If so, they may have been the seeds of the observed supermassive black hole. The very massive primordial black holes would have grown by accretion of ordinary matter and black hole mergers.
- Summary:
So there are ways of making black holes.
-
Question: Is there any observational evidence for
black holes.
- Yes, a lot.
- None at all.
Answer 1 is right.In fact, we have already discussed the evidence for stellar mass black holes from the gravitational wave events (see The Gravitational Wave Test for Black Holes above) and for supermassive black holes (SMBHs) from direct imaging (see subsection Almost Certainly Black Holes Exist Due to Direct Observation above).
But what of evidence for the general population of black holes?
We take up this evidence below in the sections Stellar-Mass Black Holes and Supermassive Black Holes.
- Stellar Mass Black Holes from Compact Star Mergers:
In principle, a black hole of any mass can exist.
If you compact an object to within its predicted event horizon for its mass as determined by the Schwarzschild radius formula or Kerr-Schwarzschild radius formula, then the object in theory must become a black hole. In fact, general relativity tells us that runaway gravitational collapse to the black hole singularity must occur which we do NOT think happens. Quantum gravity effects probably stop the runaway gravitational collapse at some point in some way that we do NOT know.
Such compaction requires tremendous force (before the runaway starts) and according to conventional thinking that force can only be supplied by the self-gravity of some massive objects that lose their pressure support somehow.
-
However, there is some unconventional thinking.
See section Micro Black Holes below.
So let's consider the ways to make the various types black holes as categorized by mass: stellar mass black holes (≤ 100 M_☉), intermediate-mass black holes (in range 100 to 10**5 M_☉), and supermassive black holes (≥ 10**5 M_☉).
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 25 problems 2--7 on black holes, Schwarzschild solution, Kerr solution, event horizon, and the gravitational singularity.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 25.
- Stellar-Mass Black Holes
-
Stellar-mass black holes
are black holes
are those of a few to a few tens of
solar masses.
These are the ones that give rise to the
gravitational wave events
from black hole mergers.
- Isolated Black Holes:
An isolated black hole is a pretty hard object to detect. But there are ways.
Ways isolated black holes can be detected:
- Via Up Close Observation:
If you were up close, you could see it as a black hole in the sky as in the figure below (local link / general link: black_hole_isolated_up_close.html).
- Via Gravitational Microlensing Events:
Isolated black holes can be detected by their gravitational effect via gravitational microlensing: the gravitational lensing by stars or smaller astronomical object.
What happens is you see a brightening of a background star due to an invisible foreground astronomical object that gravitationally focuses the background star's light in a event of unresolved gravitational microlensing. The situation is illustrated in the figure below (local link / general link: gravitational_lensing.html).
The animation in the figure below (local link / general link: black_hole_gravitational_lensing.html). shows an artist conception of gravitational lensing (but NOT gravitational microlensing) for a very nearby black hole passing in front of a background galaxy---something we are never likely to see.
- Via Hawking Radiation:
Isolated black holes would maybe emit Hawking radiation as we discuss the section Hawking Radiation.
But NO one has ever suggested that that would be observed any time soon in any direct observation. Indirect observations may be possible.
- Via Gravitational Microlensing Events:
- Black Holes in Binaries:
Stellar-mass black holes in binaries that accrete mass from the companion star can become observable since the accreta emits electromagnetic radiation.
-
Question: What is the accreta made of?
- mostly hydrogen and helium or just helium in some cases.
- mostly carbon and hydrogen.
- uranium and plutonium.
Answer 1 is right.About 98 % or so of the matter in stars is hydrogen and helium. So the mass transferred to the accretion disk is likely mainly hydrogen and helium.
Some stars have lost most of their hydrogen in strong stellar winds. From such stars, the transferred mass may be mostly helium.
The abundance of metals can range from 4 % (HI-414) down to 0.0003 % (using iron as a proxy for overall metallacity) for extremely metal-poor stars (e.g., HE 1327-2326). So only a trace of metals is likely to be in the accreta.
-
Question: Why does the accreta emit?
- It becomes hot and emits approximately blackbody radiation.
- It becomes cold and emits approximately blackbody radiation.
Answer 1 is right.The accreta compacts into an accretion disk as it swirls into the black hole. The compact turns some of its kinetic energy into heat energy and its temperature becomes of order 30*10**6 K (HZ-54).
Note, blackbody radiation is the special case of thermal radiation when the emitter is at uniform temperature and has a high enough density.
Accretion disks around black holes probably usually have rather strong continuum variation in temperature, and so emit mostly a continuum mixture of of blackbody radiation of varying temperature.
So their net thermal radiation has a complex average of blackbody spectra.
HOWEVER there is also non-thermal radiation in many cases and/or phases.
This non-thermal radiation is one or both of synchrotron radiation and inverse Compton scattering radiation.
It's all a rather complex story actually: see Remillard & McClintock 2006, p. 26--28.
The latter case might happen when the companion star has puffed up to be a red giant for example and exceeded its Roche limit. The Roche limit for an astro-body is the radius which if it extends beyond it can be gravitationally pulled apart.
See the figure below (local link / general link: black_hole_accretion_disk.html) for a black hole with an accretion disk.
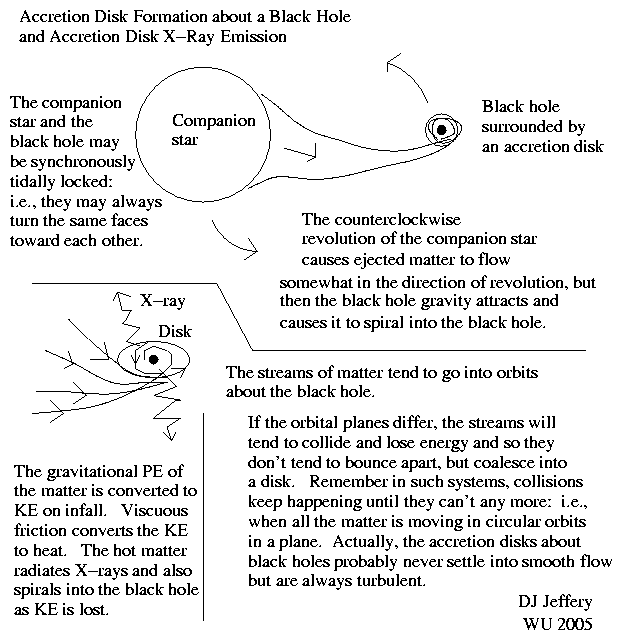
Caption: Accretion disk formation about a black hole and accretion disk X-ray emission.
Matter spirals into the black hole and energy changes from gravitational potential energy to kinetic energy of infall and rotation and then, by accretion disk viscosity, partially to heat energy which then gets emitted as X-ray emission. As we will discuss below in section Jets from Black Holes, some of the gravitational potential energy gets converted into the energy of the relativistic bipolar jets by means of magnetic fields.
Note in the visible band, an accretion disk probably looks blue since its approximate blackbody spectrum rises going blueward to peak in the X-ray band.
Credit/Permission: © David Jeffery, 2005 / Own work.
Image link: Itself.
See also the video Black hole destroying a star | 1:45 in Black hole videos below (local link / general link: black_hole_videos.html):
- EOF
As a crude approximation, we can estimate the average temperature of the accretion disk by applying the inverse Wien's law which is given in the figure below below (local link / general link: wien_law.html).
-
Note, Wien's law
is NOT adequate for
non-thermal radiation from
accretion disks: i.e.,
synchrotron radiation
and
inverse Compton scattering
radiation
(see Remillard & McClintock 2006, p. 26--28).
But let's NOT worry about those cases which are probably have temperatures that are of order those obtained for cases with thermal radiation anyway.
Given lambda_max = of order 1 Angstrom = 10**(-4) microns for X-rays from a black hole accretion disk (HZ-54), then by Wien's law
T = of order 30*10**6 K
which is of order the temperature of the center of the Sun: 16*10**6 K (Cox-54).At these temperatures, the accreta would be completely or almost completely ionized.
Note in the visible band, an accretion disk probably looks blue since its approximate blackbody spectrum rises going blueward to peak in the X-ray band.
- X-Ray Source Cygnus X-1:
Intense astrophysical X-ray sources can be caused by stellar mass black holes in binary systems as explained above in subsection Black Holes in Binaries.
But the Earth's atmosphere is largely opaque in the X-ray band (fiducial range 0.1--100 Å), and so discovery and observation of extrasolar astrophysical X-ray sources had to wait for first X-ray astronomy satellite the Uhuru satellite (1970--1973).
-
Question: Uhuru:
- means freedom in Swahili.
- was the communications officer on the original Star Trek (1966--1969).
Both answers are right.The Uhuru satellite was launched off the coast Kenya on 1970 Dec12 by NASA, and was named Uhuru to honor Kenya's independence (ST-371).
It's hard to believe the popularization of the word by Star Trek didn't play a role in the naming decision. OK, the character in Star Trek was Uhura, but it was a variation on Uhuru---so after 50 years, yours truly forgot.
-
Question: Cygnus X-1 is in the
constellation:
Answer 1 is right.X-1 means X-ray source 1, of course.
One of the main reasons for this was that the size of the hypothesized accretion disk (which is the direct source of the X-rays) could be estimated and the estimate of ∼ 3000 km is reasonable for an accretion disk orbiting a compact star of order a few tens of kilometers.
The estimate is based on the fact that Cygnus X-1 flickers on time scales as short as of order 0.01 seconds (FK-540). The figure below (local link / general link: size_time.html) shows how the flicker time scale gives a size scale of ∼ 3000 km for the accretion disk.
Cygnus X-1's companion is a O9.7 Iab (i.e., a post-main-sequence blue supergiant of luminosity class Iab). Stars that become blue supergiants typically have lifetimes of ⪅ 15 million years and masses of ⪆ 15 M_☉. (See A Table of Approximate Main Sequence Lifetimes or star_lifetimes.html, neither of which is an ideal reference.)
-
Question: Because the progenitor
of Cygnus X-1 was born
at the same time as the companion and in theory went
supernova
to create Cygnus X-1, the progenitor must have been:
- more massive than the companion originally.
- less massive than the companion originally.
- the same mass as the companion originally.
Answer 1 is right.Remember that in general, the more massive the star, the faster it goes through all its life phases (see star_main_sequence_rule.html).
But is Cygnus X-1 (meaning the compact star) a black hole or is it just a neutron star?
Early work suggested Cygnus X-1 had lower limit on its mass of ∼ 3 M_☉ (FK-541) and this overlapped with the older conventional upper limit on ∼ 3 M_☉. So being a neutron star was considered just barely possible.
However, nowadays the Cygnus X-1 has been determined to be 14.8(1.0) M_☉ (see Wikipedia: Cygnus X-1: Compact object) and the favored maximum neutron star mass ∼ 2.2 M_☉ (but with some uncertain uncertainty). So it is now clear Cygnus X-1 is a black hole beyond almost all doubt.
How big is the event horizon of Cygnus X-1? Recall the formula for the Schwarzschild radius:
R_sch = 2GM/c**2 = 2.95423 (M/M_☉) km ≅ 3 (M/M_☉) km .
Thus, if the Cygnus X-1 is a pure Schwarzschild black hole, its event horizon has a radius of about 45 km for a mass of 14.8(1.0) M_☉ (see Wikipedia: Cygnus X-1: Compact object). Actually, Cygnus X-1 must have some angular momentum, and so its event horizon radius is a bit smaller as dictated by the Kerr-Schwarzschild radius.- Stellar Mass Black Holes and Black Hole Candidates in General:
Circa 2025, there are 25 stellar mass black holes or stellar mass black hole candidates known from astrophysical X-ray sources or by other means (see Wikipedia: List of stellar mass black hole candidates; Wikipedia: Stellar black hole: Candidates). Note, the black hole candidates are those compact stars that could be either black holes or neutron stars.
Why so few?
We estimate that there must tens of thousand or more ??? black holes in the Milky Way, but most are unobservable. Only black holes in close binaries with a binary companion in a mass-losing phase will be astrophysical X-ray sources. We estimate that such objects are only a tiny fraction ??? of all black holes.
- Via Up Close Observation:
We discussed their formation in subsections Stellar Mass Black Holes from Core Collapse Supernovae and Stellar Mass Black Holes from Compact Star Mergers.
In this section, we will consider stellar mass black holes and their detection.
- Jets from Black Holes
-
Stellar mass black hole
accreting matter from a close
binary companion
will have relativistic bipolar jets
of glowing gas (hydrogen and
helium mainly,
of course) extending several parsecs from close to, but above, their
event horizons.
These jets initially move at close to the vacuum light speed (FK-542). They are relativistic bipolar jets.
See the cartoon of relativistic bipolar jets in the figure below.
Caption: A cartoon of the region surrounding a mass-accreting black hole.
Credit/Permission: © David Jeffery, 2005 / Own work.
Image link: Itself.
The jets stream out along the axis of rotation.
Electric and magnetic fields that form in the accretion disk cause the jets in some way---and that is all we will say about that.
What causes the electric and magnetic fields? The accreta is all ionized plasma. In the rotating turbulent plasma, electrical currents form in some complicated way and then they create complicated electric and magnetic fields in further complicated ways.
The energy for the jets ultimately comes from the gravitational potential energy of the material spiraling into the black holes.
Some of this gravitational potential energy becomes the heat energy of the accretion disk and gets radiated away as X-rays and some becomes the kinetic energy of the jets.
- Supermassive Black Holes
- Where Are the Supermassive Black Holes?:
During the formation of galaxies, it is believed that supermassive black holes (SMBHs) form in the galaxy centers as discussed in subsection The Formation of Supermassive Black Holes. Recall the "center" is probably the galaxy center of mass or nearly, but NO reference seems to spit out this factoid.
In fact, the current hypothesis is that nearly all large galaxies have supermassive black holes near their centers (see Wikipedia: Supermassive black holes). Evidence for this has been growing since the 1970s.
One major piece of evidence is vast radio-emitting radio lobes (beginning from relativistic bipolar jets) that emerge from the centers of some galaxies. The jets extend tens of kiloparsecs (FK-542). See the figure below.
The relativistic bipolar jets seem like scaled-up versions of the jets that emerge from stellar mass black holes.
The relativistic bipolar jets are powered by giant accretion disks that form from inflow to the centers of galaxies from within the galaxies and from the intergalactic medium (IGM).

Caption: "Color composite image of Centaurus A, revealing the radio lobes and relativistic bipolar jets emanating from the active galaxy's central supermassive black hole. This is a composite of images obtained with three instruments, operating at very different wavelengths. The 870-micron submillimeter data, from LABOCA on APEX, are shown in orange. X-ray data from the Chandra X-ray Observatory are shown in blue. Visible light data from the Wide Field Imager (WFI) on the MPG/ESO 2.2 m telescope located at La Silla Observatory, Chile, show the background stars and the galaxy's characteristic dust lane in close to "true colour." (Slightly edited.)
Credit/Permission: © ESO/WFI (optical); MPIfR/ESO/APEX/A.Weiss et al. (submillimeter); NASA/CXC/CfA)/R.Kraft et al. (X-ray), circa or before 2009 / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia: File:ESO Centaurus A LABOCA.jpg.
- Accretion Disks and Masses:
The Hubble Space Telescope (HST) has been able to resolve accretion disks of dust and gas around the central objects from which the jets seem to emerge (FK-542). The accretion disks can be of order hundreds of parsecs in size scale.
The disk rotation speeds can be determined from spectroscopy using the Doppler effect.
The determined speeds are of order hundreds of kilometers per second.
Recall v_orbital=sqrt(GM/r) is the Newtonian physics formula for the velocity of a circular orbit. Well away from the event horizon this formula is good for black holes. Inverting for mass we get v_orbital**2 * r M = __________________ G = 23.2*10**9 M_☉ (v_orbital/100 km/s)**2 * (r/100 pc) where the formula is rewritten in terms of fiducial quantities. So such central galaxy supermassive black holes can have masses up to of order 20*10**9 M_☉.In fact, the determined masses of central galaxy compact objects are determined to range from about 10**5 M_☉ to about 10**10 M_☉ (FK-542).
These masses are, however, probably much smaller than the total galaxy mass in most cases.
And supermassive black holes are still really tiny by comparison to interstellar distances. See the insert below (local link / general link: black_hole_schwarzschild_radius_formulae.html)
- EOF
- Supermassive Black Holes, AGNs, and Feedback:
But despite their relative small mass and size compared to galaxies, the supermassive black holes do have dramatic visual effects and it is thought probably have a large feedback effect on galaxy evolution.
To elaborate on their visual effects, just as stellar mass black hole can be emitters of electromagnetic radiation from their accretion disks, so can the supermassive black hole in visual and radio in particular from theirs. The supermassive black hole. are the engines of this emission. See figure below.
The stronger emitters cause their host galaxies to be classified as having AGNs (active galactic nuclei) which have strong electromagnetic radiation from their center region---the AGNs.
-
Note, the acronym
AGN
is now far more widely used than the full name
active galactic nuclei.
Matter spirals into the compact object and energy changes from gravitational potential energy to kinetic energy of infall and rotation and then, by accretion disk viscosity, partially to heat energy which then gets emitted as electromagnetic radiation. Some of the gravitational potential energy gets converted into the energy of the relativistic bipolar jets by means of magnetic fields.
See the illustrative figure below.

Caption: "This artist's conception depicts a supermassive black hole at the center of a galaxy. NASA's GALEX spacecraft found evidence that supermassive black holes---once they grow to a critical size---stifle the formation of new stars in elliptical galaxies. supermassive black holes are thought to do this by heating up and blasting away the gas that fuels star formation. The blue color here represents radiation pouring out from material very close to the supermassive black hole (i.e., from the accretion disk). The grayish structure surrounding the supermassive black hole, called a torus, is made up of gas and dust. Beyond the torus, only the old red-colored stars that make up the elliptical galaxy can be seen. There are no new stars in the elliptical galaxy."
Note, the relativistic bipolar jets of which one is hidden by the accretion disk and torus.
Credit/Permission: NASA/Jet Propulsion Laboratory (JPL)-Caltech, circa or before 2007 / Public domain.
Image link: Wikipedia: File:Supermassiveblackhole nasajpl.jpg.
- Quasars:
The most extreme of the AGNs are quasars which look like point sources, but have cosmological redshifts that put them at distances of thousands of megaparsecs (i.e., at billions of light-years), and therefore in an earlier stage of the observable universe billions of years ago.
-
Cosmological redshifts
and their relation to distance will be taken up in
IAL 30: Cosmology.
-
Because quasars are
point sources, we do NOT observationally detect their
host galaxies in most cases.
However, the high resolution images
from the
Hubble Space Telescope (HST, 1990--2040?, d = 2.4 m, Cassegrain reflector)
and other instruments show they have
host galaxies as was always thought.
(Wikipedia: Quasars).
Quasars look star-like because their emission regions (i.e., their accretion disks) are small relative to that of galaxies.
Quasars and their accretion disks are illustrated in the two figures below ( (local link / general link: agn_quasar_3C_273.html; unlinked).

Caption: "A growing black hole, called a quasar, can be seen at the center of a faraway galaxy in this artist's concept. Astronomers using NASA's Spitzer and Chandra space telescopes discovered swarms of similar quasars hiding in dusty galaxies in the distant universe. The quasar is the orange object at the center of the large, irregular-shaped galaxy. It consists of a dusty, doughnut-shaped cloud of gas and dust that feeds a central supermassive black holes. As the black hole feeds, the gas and dust heat up and spray out X-rays, as illustrated by the white rays. Beyond the quasar, stars can be seen forming in clumps throughout the galaxy. Other similar galaxies hosting quasars are visible in the background."
Credit/Permission: NASA, 2007 (uploaded to Wikipedia by User:TheDJ, 2008) / Public domain.
Download site: PIA10093: Bursting with Stars and Black Holes (Artist Concept).
Image link: Wikipedia: File:Black hole quasar NASA.jpg.
For more insight in quasar behavior see Quasar videos below:
- Quasar | 0:26: A quasar with relativistic bipolar jets. You have to scroll down for it. Good for the classroom.
- Quasar in a Primeval Galaxy (or Protogalaxy) | 3:20: Too long for the classroom.
-
Quasar videos
(i.e., Quasar
videos):
Quasar luminosity ranges from 10**38 to 10**42 W (FK-613). Recall the Sun has L_☉ = 3.845*10**26 W (Cox-340). The total luminosity of the Milky Way is about 10**37 W (FK-613).The brightest quasars may have to consume up to 500 M_☉/year of mass in order to shine (FK-613; HI-456).Quasars it seems were most abundant about 12 Gyr ago and became rare about 7 Gyr ago. They are found in the cosmological redshift z range 0.056--7.54 corresponding to comoving distances (i.e., physical distance measured at our current cosmic time) ∼ 200 Mpc ≅ 600 Mly to ∼ 10 Gpc ≅ 30 Gly and lookback times ∼ 0.5 Gyr to 13 Gyr (see Wikipedia: Quasar: Properties; Ned Wright's cosmic calculator).
Note, there are NO quasars in the very local observable universe (i.e., z ⪅ 0.06, r ⪅ 200 Mpc, lookback time ⪅ 0.5 Gyr ). So they are extinct in the current/modern observable universe. But, of course, we see them since we can see the past---the farther you look out, the farther back in cosmic time you see.
-
Question: Why are there no
quasars
in the
local observable universe
(i.e., in the modern universe)
as out to z ≅ 0.06 (r ≅ 200 Mpc).
- They used up most of the gas and stars in their immediate vicinity that they were fueled by, and so went out. For some reason, this fuel was NEVER sufficiently replenished by infall from the intergalactic medium (IGM).
- They used up their nuclear burning fuel.
Answer 1 is right.The supermassive black holes at the center of the quasar galaxies still exist, but they are NO longer fed well enough to be quasars.
The Milky Way itself has a central supermassive black hole which we discussed in subsection More Evidence from the Milky Way and Sgr A* above and we will discuss more fully in IAL 27: The Milky Way.
Here we will say that Galactic central black hole is in the radio source Sagittarius A* (Sgr A*) (the asterisk being pronounced "star") near the dynamic center of the Milky Way, and so is sometimes just called Sagittarius A*
The Sagittarius A* is 7.860(180) kpc away (Wikipedia: Sagittarius A*).
The measured mass of the Sagittarius A* is about 4*10**6 M_☉ and its Schwarzschild radius is ∼ 0.1 AU.
Supermassive black holes in the centers of galaxies actually have a profound effect on the evolution of the observable universe as discussed in the figure below (local link / general link: m_sigma_relation.html).
- Accretion Disks and Masses:
- Hawking Radiation
-
In the 1970s,
Stephen Hawking (1942--2018)
(see figure below:
local link /
general link: stephen_hawking.html)
discovered a process by which
black holes
could emit particles from outside the
event horizon---and so lose
mass-energy---which
was NOT thought possible before.
- The Process of Hawking Radiation:
The escape process is now called Hawking radiation (FK-549; CK-361; HI-362).
From quantum mechanics, we know that the vacuum is active: it is NOT just inactive nothingness.
What are called virtual particles are coming into "existence" and vanishing without out a directly observable trace all the time everywhere: the vacuum is seething with them.
The virtual particles come into "existence" in pairs: e.g., proton and antiproton, electron and antielectron (i.e., positron), photon and photon (the photon is its own antiparticle) (FK-549). A pair consists of a particle and its antiparticle in order to conserve various properties: e.g., electric charge.
The virtual particles "exist" for of order 10**(-21) s (CK-361). Then they mutually annihilate as matter and antimatter are supposed to do.
-
"Existence" above is in quotation marks because the
virtual particles
CANNOT be directly detected in principle, but they have indirect effects that
can be observed and those effects are well verified.
-
As usual, we don't go into details and just say things may happen if
their is enough energy.
When they do so "appear" there, sometimes the pairs just annihilate.
Sometimes they will both fall into the event horizon: their gravitational potential energy is converted into enough energy to make them "real", but they are lost in the black hole anyway.
But sometimes one of the pair will fall in and the conversion of some of the black hole's gravitational field energy is used to make the other one of the pair "real" and give it escape velocity.
The particles are actually pulled apart and made "real" by the tidal force of the black hole.
See the cartoon Hawking radiation figure below.
Caption: A cartoon of Hawking radiation from a black hole.
Credit/Permission: © David Jeffery, 2005 / Own work.
Image link: Itself.
So one of the pair of virtual particles becomes "real" and escapes to infinity. It is a particle of Hawking radiation.
The mass-energy of the escaping particle comes at the expense of the mass-energy of the black hole.
So the black hole loses mass-energy by Hawking radiation---but from outside the event horizon---nothing gets out through the event horizon.
-
Hawking radiation videos
(i.e., Hawking radiation
videos):
- Hawking Radiation | 0:32: I won't attest to its authoritativeness, but it looks OK. One sees the binary companion, the accretion disk, the relativistic jet, the hot spot where the accreta hits the accretion disk, the black hole, and schematic Hawking radiation. Short enough for the classroom.
- BBC documentary explaining Hawking radiation | 6:31: Maybe authoritative. Too long for the classroom.
- The Paradox of Hawking Radiation:
It's sounds paradoxical, but it seems true: mass-energy can escape from inside the event horizon, but NOT by going through the event horizon. This escape process does NOT occur in general relativity---it is strictly a result of quantum mechanics.
In fact, Hawking radiation is strange in that it relies on two theories which are NOT formally consistent: general relativity and quantum mechanics.
However, we believe that such strange mixtures can be (but NOT necessarily are) correct, if both theories are on the right path. We hope that quantum gravity will someday verify the mixture---or disprove it and show what is right.
But for the time being, Hawking radiation seems an unescapable consequence of what we think are true theories---general relativity being an emergent theory.
No one can think of plausible reason why Hawking radiation should NOT happen.
- Observing Hawking Radiation:
Hawking radiation is potentially observable.
The photon emission is probably completely unobservable until a very late phase: see below.
However, antiprotons of a specific range of energy from Hawking radiation should contribute to the cosmic rays that constantly bombard the Earth.
-
Cosmic rays
are been known since 1912 are probably
protons,
alpha particles (He-4 nuclei),
heavier nuclei, electrons, and a small fraction of
positrons
and
antiprotons
(Wikipedia: Cosmic Rays: Composition;
Gr-424--425).
They permeate intra-galactic space.
They are probably mostly produced somehow by supernovae.
Cosmic rays travel at near the vacuum light speed.
When they impact the Earth's atmosphere, they create a cascade of other particles by nuclear and ionization reactions: these other particles include proton, electrons, neutrons, mesons and gamma rays. See the illustrative figure below.

Caption: "When cosmic rays enter the Earth's atmosphere, they collide with molecules, mainly oxygen (O_2) and nitrogen (N_2), to produce a cascade of billions of lighter particles, a so-called air shower. All of the produced particles stay within about one degree of the primary particle's path. Typical particles produced in such collisions are charged mesons, e.g., positive and negative pions and kaons. These subsequently decay into muons that are easily detected by many types of particle detectors."
So a single primary, high-energy cosmic rays can create a shower of other particles at the Earth's surface and it is those other particles that are observed.
Credit/Permission: © User:SyntaxError55 / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia: File:Atmospheric Collision.svg.
However, if Hawking radiation exists and contributes to cosmic rays, there are other sources for cosmic rays and we CANNOT so far distinguish the hypothetical Hawking radiation cosmic rays from other cosmic rays. So at present, cosmic rays do NOT provide evidence for Hawking radiation.
- Black Hole Evaporation:
If black holes can lose mass by Hawking radiation, can they evaporate entirely?
In principle, yes.
It turns out that the main component of Hawking radiation is blackbody radiation (see John Baez, Hawking Radiation).
This means the emitted photons have a blackbody spectrum and that there is a black hole temperature.
The black hole temperature is inversely proportional to the mass:
6*10**(-8) K T = approximately ----------------- . M / M_☉So black holes of stellar mass are very cold and have very low emission rates.
In fact, black hole luminosity in Hawking radiation decreases with mass:
L_black_hole proportional to 1/M**2
(see Wikipedia: Hawking radiation: Black hole evaporation).The upshot is that black holes lose mass-energy slowly at first and then more and more rapidly until they evaporate altogether.
-
There is a controversial theory that
black holes do NOT
evaporate entirely
(Ellis, G. F. R. 2013, arXiv:1310.4771 [gr-qc],
Ellis, G. F. R. 2013, arXiv:1311.0595 [gr-qc]).
There will always be a remnant black hole.
At the moment, the theory has won few converts. Time will tell if it gains any traction.
__________________________________________________________________________ Table: Black Hole Mass, Temperature, and Evaporation Time __________________________________________________________________________ Initial Mass Initial Temperature Order of Time to Evaporation __________________________________________________________________________ 5*10**6 M_☉ 10**(-13) K 10**80 years 5 M_☉ ≅ 10**31 kg 10**(-7) K 10**62 years 10**15 kg 10**9 K 10**33 years 10**10 kg 10**14 K 15 Gyr (of order of the Mount Everest mass) ___________________________________________________________________________ Reference: FK-549--550. ___________________________________________________________________________
The acceleration of the rate of Hawking radiation as the mass of the black holes approaches zero is expected to give rise to an explosive event with an energy release of order 10**9 Megatons TNT (FK-550).Some of this energy would be in the form of electromagnetic radiation (maybe primarily gamma rays???), and so the final demise should be observable in principle.
Recall that Hawking also suggested that small primordial black holes with masses from about 5*10**(-8) kg to Earth mass could have been formed in the Big Bang which occurred of order 14 Gyr ago (FK-544).
Some of these primordial black holes should be ending their existence right now in explosions if they exist.
In fact, Hawking probably originally thought of the idea of small primordial black holes because if they exist, they are available to prove Hawking radiation observationally.
There is NO evidence yet for such explosions from small primordial black holes. They may NOT exist or we may NOT yet have the right methods to detect them.
The idea that evaporating small primordial black holes could be one source of gamma ray bursts seems to be highly DISFAVORED (see Wikipedia: Primordial black holes: Implications).
- The Black Hole Firewall Paradox:
For the black hole firewall paradox, see the insert above (local link / general link: black_hole_arcane_problems.html) on Arcane Problems with Black Holes.
Note, the mass-energy does NOT escape through the event horizon---nothing does we think.
- Appendix: Micro Black Holes (Not Required for the RHST)
-
There are some
quantum gravity theories
that predict that
gravity should actually become very strong on very small
size scales (up to maybe 10**(-4) m), but size scales much bigger than the
Planck length
(Gr-400,407,424--426).
- Detecting Micro Black Holes
with the LHC:
The Large Hadron Collider (LHC), which is currently in operation and straddles the Swiss-French border west of Geneva, may be able to produce micro black holes in a controlled and therefore noticeable way.
Micro black holes created by LHC would decay almost immediately by Hawking radiation, but presumably they would give detectable signatures in their decay particles (Gr-403).
-
The
LHC
is operated by the European agency CERN
(an acronym for Conseil Europeen pour la Recherche Nucleaire
the original name is almost forgotten).
A hadron is a particle that experiences the strong nuclear force: the commonest examples are the proton and neutron.
The figure below displays one of the key instruments of the LHC.

Caption: "Construction of one detector (called CMS) of the Large Hadron Collider (LHC) at CERN (2003)."
Credit/Permission: © User:Freerk, 2003 (uploaded to Wikipedia by User:Square87~commonswiki, 2005) / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia: File:Construction of LHC at CERN.jpg.
-
Large Hadron Collider (LHC) videos:
- LHC Collides At Record Speeds, 2010 | 1:57: Out of date news now, but it gives a quick look at the way things look at the LHC and shows beamline collisions in artist's conception. With scrolling to good bits, OK for the classroom. The curved paths of some of the outgoing particles is because they are charged particles and charged particles follow curved paths in magnetic fields and there is a magnetic field in the beamline. Short enough with cuts for the classroom.
- The LHC - The Large Hadron Collider (LHC), 2008, | 6:15: How it works. Too long for classroom.
- Tim Berners-Lee:
The World Wide Web: who is responsible? See the figure below (local link / general link: tim_berners_lee.html).
- Detecting Micro Black Holes from Cosmic Rays:
The strongest cosmic rays would similarly produce micro black holes that would be detected by the showers of particles they would create.
The Pierre Auger Observatory (a cosmic ray observatory covering about 3000 km**2 in Argentina) may detect such showers.
-
A cosmic ray observatory is just an array of particle detectors
spread over an area. The detector captures some portion of the
air shower of
particles that cascade from a single
cosmic ray
and allows the original
cosmic ray
to be characterized.
-
The
Planck length
(which is a fundamental length in
quantum mechanics)
is given by
Planck length = sqrt(G*ħ/c**3) = (1.616255(18))*10**(-35) m , where c is the vacuum light speed, G is the gravitational constant, and ħ (h with a stroke through it vocalized h-bar) is the Planck constant divided by 2*π (CL-123).
If these theories are right---and they are probably NOT----then it is possible that micro black holes (of mass of order 1000 proton masses) could be produced in current/future giant accelerators and are being produced all the time by the strongest cosmic rays that impact on the Earth's atmosphere.If micro black holes exist and are produced by the strongest cosmic rays, they CANNOT be dangerous since we do NOT notice them.
If they were detected, we have another strong evidence that black holes exist in general, that that Hawking radiation exists, and that we are on some kind of right path to a quantum gravity theory.
We should expect NO such revelation---but you never know, maybe it will happen.
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 25 problems 8--13 on black holes, stellar mass black holes, bipolar jets, supermassive black hole, and Hawking radiation.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 25.
- Special Relativity (Reading Only)

