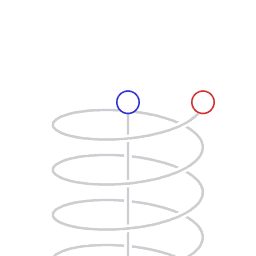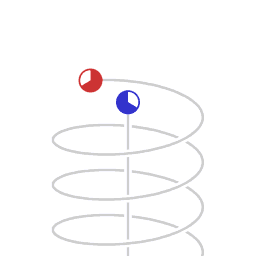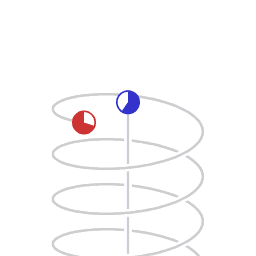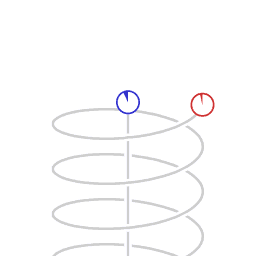
Caption: An animation illustrating time dilation (more precisely, special relativistic time dilation) and the asymmetry in time dilation between inertial frame motion and non-inertial frame motion (i.e., a motion with an acceleration relative to an inertial frame). Note time dilation is mnemonicked by saying "Moving clocks run slow."

Features:

1. The animation shows the a 2-clock system in a Minkowski diagram (AKA spacetime diagram).

2. The horizontal is a plane in physical space and the vertical is the time dimension.

3. The Minkowski diagram is for the reference frame of the stationary clock (which is the blue clock).

   This reference frame is an inertial frame.

   The reference frame of the moving clock (which is the red clock) is a non-inertial frame because it is an accelerated frame relative to an inertial frame: in this case, the inertial frame of the stationary clock.

4. The upward motion of both clocks is a motion forward in time.

   The spiraling of the moving clock is actually a circling in physical space.

   The paths of the clocks are their world lines in Relativityspeak.

5. With a bit of staring you see that the moving clock runs slow compared to the stationary clock. As aforesaid, time dilation is, in fact, mnemonicked by saying "Moving clocks run slow."

6. All clocks moving with the moving clock run slow: mechanical clocks, atomic clocks, biological clocks, all clocks.

   Time itself runs slow in the moving clock's reference frame relative to the reference frame of the stationary clock.

7. But there is a seeming paradox: should NOT the stationary clock run slow compared to the moving clock if motion is all relative?

   Actually, all motion is NOT relative in special relativity.

   Acceleration relative to an inertial frame is distinct from constant velocity motion relative to an inertial frame.

   The moving clock is accelerated continuously since its direction of the motion is continuously changing even though its speed is constant.

   The asymmetry between accelerated and non-accelerated motion is the origin in this case of the time dilation difference between the two clocks.

8. The situation of the two clocks is an example of the twin paradox.

   The clocks are twins: the traveling twin ages less than the unmoving twin.

9. The twin paradox has been verified many times using two atomic clocks: one is kept at one place on Earth and the other is sent around the Earth on a jet. Less time passes for the atomic clock on the jet.

   However, there is a gravitational time dilation that must be accounted for as well for the atomic clock-jet.

10. Time dilation and gravitational time dilation are NOT just of scientific interest.

    They are very small effects in most of everyday life, but the Global Positioning System (GPS) would NOT work nearly as accurately as it does without accounting for both time dilation and gravitational time dilation.

11. There is, of course, time dilation between clocks both moving at constant velocity relative to an inertial frame.

    To understand this, define an inertial frame as the rest frame and cover it with synchronized stationary clocks. They stay synchronized as time passes, but do NOT move in space relative to each other or the inertial frame.

    Now consider a clock moving at constant velocity relative to the rest frame.

    The moving clock, though at rest in its own reference frame, is moving in space as well as time relative to the stationary clocks.

    In special relativity, space and time motions interact and the formalism of special relativity predicts that the moving clock runs slow compared to the stationary clocks.

    A second set of clocks covering the reference frame of the moving clock (which is an inertial frame too) would show that any one of the stationary clocks runs slow compared to the second set.

    So the situation is symmetrical between the defined rest and moving frame. The motion between them is indeed relative.

    No contradictions arise from this symmetry, but we have NOT shown that which takes some effort---which yours truly has never done.

12. The special relativistic time dilation formula for constant velocity relative to an inertial frame defined as the rest frame is

        Δt' = Δt*sqrt(1-β**2) ,

    where Δt' is the time interval for the moving clock between 2 spacetime points, Δt is the time interval in the defined rest frame between the same 2 spacetime points, and β = v/c, where v is the speed of the constant velocity.

    The time intervals Δt' and Δt are just what clocks in the moving frame and rest frame would measure: all clocks: mechanical clocks, atomic clocks, biological clocks, all clocks.

    Even for very high everyday life speeds (e.g., the low-Earth orbital speed ∼ 8 km/s), β is tiny and β**2 super tiny (e.g., ∼ [8/(3*10**5)]**2 ≅ 10**(-9) for low-Earth orbital speed), and so we NEVER notice time dilation in everyday life sans (AKA without) measurements of super accuracy/precision---which can be done in some cases and those cases verify special relativity to within uncertainty.