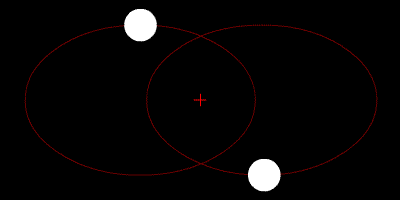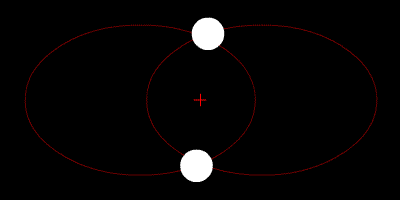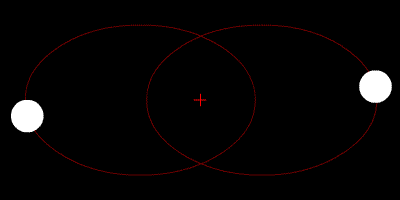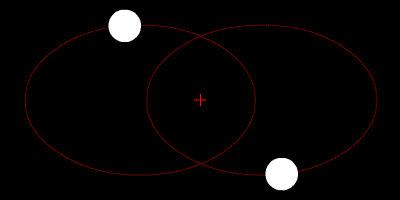
Image 1 Caption: An animation of a (gravitationally-bound) gavitational two-body system with two spherically symmetric, equal-mass astro-bodies orbiting in elliptical orbits around their common center of mass which marked by a red cross.

The star sizes are vastly exaggerated relative to the inter-star distances for most binaries---but NOT all---there are some very close binary systems.

Features of general gravitational two-body systems:

1. The center of mass is a focus for both elliptical orbits. The other focuses are just empty points in physical space with NO significant meaning.

2. The elliptical orbits of all gravitational two-body systems are determined by Newtonian physics (what is universal about the physical system) and initial conditions (what is peculiar or individual about the physical system).

3. Gravity is, of course, the force that pulls the astro-bodies into orbits.

4. The periapsis (AKA pericenter) is the arrangement of closest separation and the term is also used for the closest separation distance.

5. The apoapsis (AKA apocenter) is the arrangement of farthest separation and the term is also used for the farthest separation distance.

6. The apse line (AKA line of apsides) is drawn through the periapsis and apoapsis.

7. The relative mean orbital radius (AKA relative semi-major axis) is given by

           a=(1/2)*( r_periapsis +r_apoapsis ) , 

   where r_periapsis is the periapsis separation and r_apoapsis is the apoapsis separation.

8. In most real orbits, astronomical perturbations cause noticeable deviations from exact two-body system behavior.

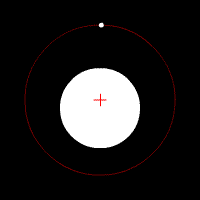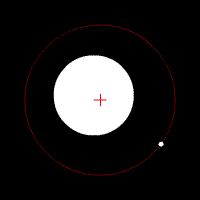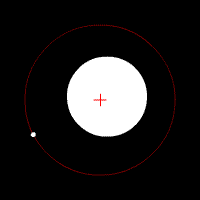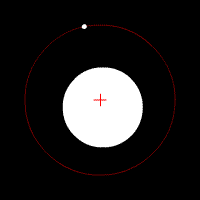
Image 2 Caption: A gravitationally-bound gavitational two-body system with a large difference in mass between the two spherically-symmetric astro-bodies orbiting in circular orbits their common center of mass which marked by a red cross.

1. If the mass of smaller body were negligible compared to that of the larger body, the more massive body would NOT be seen by the eye to be moving.

   In this case, the more massive body center would effectively be the center of mass of the gavitational two-body system.

2. For circular orbits, there is only one focus which in math jargon is to say the two focuses are mathematically degenerate.

3. The periapsis and apoapsis are also mathematically degenerate: i.e., they have been squeezed to the same value and the relative orbital radius is a contant.

4. This two-body system could be, e.g., a close binary star system a close star and planet system, or a close planet and moon system.

Images:

1. Credit/Permission: User:Zhatt, before or circa 2005 (uploaded to Wikipedia by User:Julo, 2005) / Public domain.
   Image link: Wikipedia: File:Orbit5.gif.
   
2. Credit/Permission: User:Zhatt, before or circa 2005 (uploaded to Wikipedia by User:Julo, 2005) / Public domain.
   Image link: Wikipedia: File:Orbit4.gif.