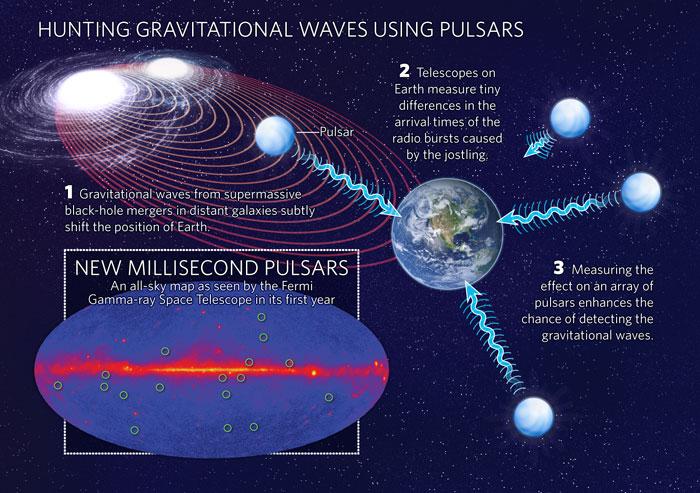
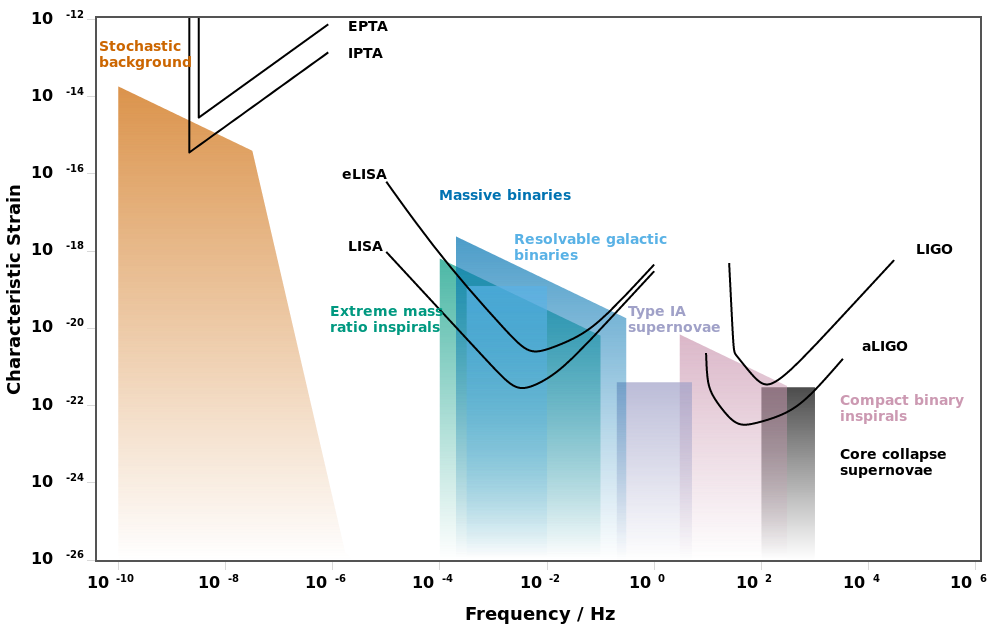
Image 4 Caption:
"An animation
of the effect of a plus-polarized
gravitational wave
on a ring of test particles."
A cross-polarized
gravitational wave
would give the same behavoir rotated by 45°.
The test particles
are in a plane
perpendicular
to the propagation direction
infinite
plane wave
gravitational waves.

Gravitational waves
as can be seen in the
animation
are
quadrupole waves
(in lowest
order to be exact).
As infinite
plane wave
gravitational waves
pass through,
space is expanded and contracted alternatively in two
perpendicular directions.
To extend the picture,
every line of test particles
aligned with one direction would expand and contract alternating with the
expansion and contraction in the other direction of
every line of test particles
aligned with the that other direction.
For ideal test particles,
the gravitational waves
lose/gain NO energy
passing through.
However, if the
test particles
interact with each other, then
energy might be
(lost to)/(gained from) some form in the
system
of the test particles.
In most actual astrophysical cases, one would expect
large gravitational waves
propagating through the
observable universe
to lose energy
in expanding non-elastic systems.
However, systems
of mutually gravitating
stars,
planets,
etc.
are probably to
1st order
elastic systems.
So such large gravitational waves
probably do NOT lose
much energy
by interacting with
local astronomical objects
as they propagate.
This makes the large
gravitational waves
very useful observables for the nature of their sources.
Note, the
energy available
to deposit in any location must go down as the
gravitational waves
expand from their sources.
There is remarkable feature about
gravitational waves.
They travel through space
making NO contribution
to energy-momentum tensor T_ij
(i.e., the right-hand side)
of Einstein field equations.
If there were NO
local mass-energy
(i.e., galaxies,
dark energy,
etc.)
as the gravitational waves
propagate, the
energy-momentum tensor T_ij
would be being zero.
Somehow gravitational waves
carry energy
and momentum NOT
in a density form (i.e., so much here, so much there), but in a nonlocal form:
i.e., the energy
and momentum are coded
into the gravitational waves
in a non-density form.
See
Roger Penrose, The Road to Reality
(2004, p. 467--468).
Another remarkable emarkable feature about
gravitational waves
is that they do NOT necessarily obey
the conservation of energy principle.
There is NO absolute proof that the
gravitational potential energy
they remove from their source
will be deposited elsewhere: it might be less or more in total.
There is a proof that gravitational waves
do obey
conservation of energy principle
in a sense in an important special case (see
Roger Penrose, The Road to Reality, 2004,
p. 467--468).
The last feature brings up an issue also related to the
first feature.
Gravitational potential energy
is NOT
actually an energy
of the gravitational field
in an ordinary sense.
Note the gravitational field
is our classical limit
way of thinking of the
curvature of spacetime
which is how gravity
is manifested in general relativity.
So the gravitational field
is NOT a field
in the sense of
the electromagnetic field
which has an associated
energy density: i.e., there
is so much energy here,
so much energy there.
If gravitational field
had an energy density,
then the gravitational field
would become self-gravitating
which would be extremely paradoxical since it is NOT
self-gravitating
in the classical limit.
Also, the simplest approach to
gravitational field
energy density leads to it having
negative mass which is really hard
to make sense of.
General relativity
avoids the paradox
by coding energy
stored in the structures of
spacetime
(e.g., gravitational waves)
nonlocally, and so it does NOT appear in
the
energy-momentum tensor T_ij
of the Einstein field equations
NOR anywhere explicitly.
You can put energy
into the structures of
spacetime
and get it out, but while in those structures
it is NOT exactly known where it is.
It can be approximately known (see
Roger Penrose, The Road to Reality, 2004,
p. 465).