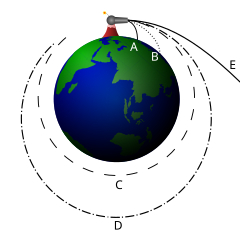
Caption: An illustration of Newton's cannonball thought experiment (or Gedanken experiment) for a projectile (e.g., a cannonball) launched from a giant mountain on the Earth. The projectile has negligible mass and size compared to the Earth (i.e., it is a test particle) and we neglect air drag.

Features:

1. The projectile is as aforesaid a test particle: i.e., an object of negligible mass compared to the Earth, and so it does NOT affect the Earth's motion at all.

2. As the image implies, as launch velocity increases (v↑), the projectile orbit is as follows:
   1. A: a parabolic trajectory crashing into the Earth.
   2. B: like A, but with a longer trajectory.
   3. C: a circular orbit,
   4. D: an elliptical orbit,
   5. E: an escape orbit which may be just at escape velocity leading to a parabolic orbit or may be above escape velocity leading to a hyperbolic orbit.

   See the mathematical description of Newton's cannonball thought experiment (or Gedanken experiment) below.

3. The image shows that being in orbit is actually being perpetually in free fall, but always NOT hitting the orbited astro-body. The literal truth.

   You keep missing because you have velocity component NOT aimed at the center of force or, in physics jargon, you have an angular momentum about the center of force. The central force by itself has NO way of removing this angular momentum: i.e., there is conservation of angular momentum in a central force system.

4. Note gravity is NOT turned off in space. It's often quite strong: e.g., in low Earth orbit, it's nearly as strong as on the Earth's surface. But if NO forces resist gravity, an astronaut and his spacecraft are in free fall: falling together under gravity and being weightless.

5. Isaac Newton (1643--1727) himself thought up Newton's cannonball and a diagram of it appeared in his book the Principia (1687) (see Wikipedia: Newton's cannonball: Other appearances).

   Note that a thought experiment (or Gedanken experiment) is an experiment that can be performed in principle and that illustrates a physical point of interest. The experiment may or may NOT be possible in practice, but usually when one calls something explicitly a thought experiment (or Gedanken experiment), one means an experiment NOT or NOT easily done in practice.

   Of course, Newton's cannonball was a pure thought experiment (or Gedanken experiment) in Newton's time, but nowadays it is done all the time with rockets, mutatis mutandis: i.e., no cannon, no cannonball, no mountain.

6. Newton's cannonball videos (i.e., Newton's cannonball videos):
   
   1. Projectiles launched horizontally into orbit (Newton's cannonball) | 0:16: With continuous variation of launch speed. Short enough for classroom.
   2. Newton's Cannon in action | 0:28: Good. Short enough for classroom.
   3. Newton's cannon animation | 0:30: With background music. Short enough for classroom.

7. Mathematical discription of Newton's cannonball thought experiment (or Gedanken experiment) with projectile launch velocity v:
   1. For v less than the low-Earth-orbit velocity v_circular ≅ 7.9 km/s, the projectile follows approximately a parabolic trajectory and crashes into Earth.
   2. For v = v_circular, the projectile goes into a circular low Earth orbit.
   3. For v_circular < v < v_escape ≅ 11.2 km/s (i.e., the escape velocity) the projectile goes into a elliptical orbit.
   4. For v = v_escape, the projectile goes into an open orbit (or an escape orbit) and escapes to infinity. It will reach infinite distance with zero velocity in infinite time if nothing else affects it. The open orbit is a parabolic orbit.
   5. For v > v_escape, the projectile goes into an open orbit (or an escape orbit) and escapes to infinity. It will reach infinite distance with greater than zero velocity in infinite time if nothing else affects it. The open orbit is a hyperbolic orbit.

8. For a reference on orbital velocity and escape velocity formulae, see file Orbit file: orbit_velocity_circular_escape.html which may be given just below if the Newton's cannonball figure has NOT been repeated:
   EOF