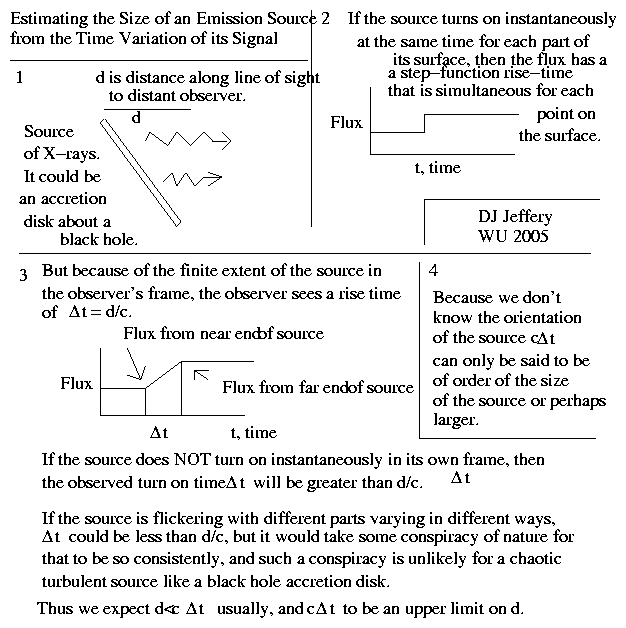
Caption: Estimating the size scale of disk emission source from the time variation of its signal. There are some glitches in figure and it seem a bit too complex.

Features:

1. The basic idea is that if the whole disk emission various synchronously in its own reference frame, the observed emission shows continuously varying time delays due to the continuously varying light travel time.

2. For example, say the disk instantly brightens in its own reference frame.

   A distant observer will observe NOT an instantaneous brightening, but a rising brightening over a time period Δt = d/c, where d is the distance along the line-of-sight between near and far ends of the disk.

   Since one measures Δt, calculates d = c*Δt.

   If one knew (and usually one does NOT know) the inclination θ of the disk (i.e., the angle between the rotation axis and the line-of-sight, one can calculate the diameter D of the disk from D = d/sin(θ).

   If θ = 90°, then D = d. If θ = 0°, then D = ∞---which is an extreme, impossible limit.

3. Usually, the disk will NOT vary in emission in any simple way and it's shape may NOT be a perfect disk. Furthermore (as indicated above), one usually does NOT know the inclination.

   In consequence, the calculated d based on a characteristic variation time for the light signal from a disk will only be a characteristic size scale.

   This means the disk diameter will be maybe d to with an order of magnitude or so.

4. Disk size scale estimation by characteristic variation time is done for accretion disk about black holes.

5. For example, X-ray source Cygnus X-1 (believed to be due due to an accretion disk about black holes) flickers on time scales as short as of order 0.01 seconds (FK-540).

   Thus, the size of the Cygnus X-1 is d = c * Δt = 3*10**5 km/s * 0.01 s = 3000 km .

   A sophisticated analysis shows that the accretion disk diameter is actually ∼ 30,000 km or 10 times as large as our crude estimate.