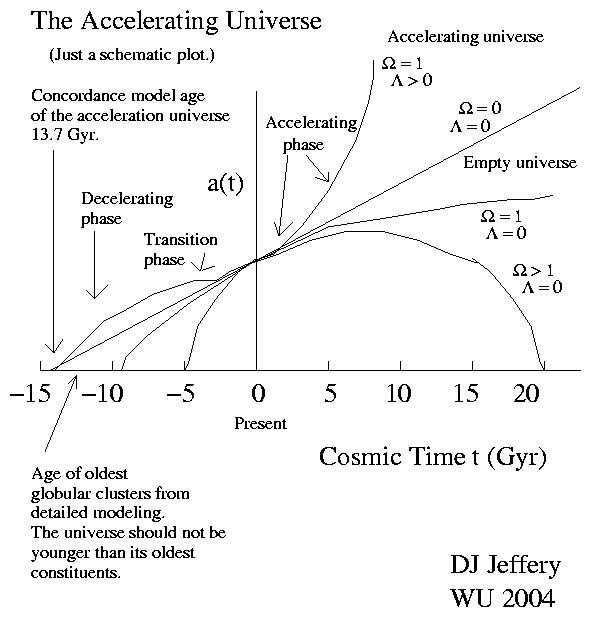
Caption: The evolution of the cosmic scale factor a(t) for 4 qualitatively distinct Friedmann equation models. One model is an accelerating universe model i.e., the Friedmann equation model with positive Lambda (i.e., Λ > 0). The other Friedmann equation models are NOT accelerating.

Features:

1. The image is just a cartoon plot that yours truly drew free hand to illustrate the 4 cosmological models.

2. The cosmic scale factor a(t) is the function of cosmic time that describes the scaling of the observable universe.

3. All (cosmological) proper distances (i.e., real physical distances that could be measured at one instant in time) scale with a(t):

         r_proper = a(t) * r_comoving ,

   where r_comoving is comovoing distance which is a time-independent set of distances.

   The cosmic present t_0 (equal to the age of the observable universe = 13.797(23) Gyr (Planck 2018)) is by convention symbolized by the subscript 0. By convention, a_0 (i.e., the present scale factor) = a(t_0) = 1, and so proper distances and comovoing distances are equal at cosmic present t_0 (equal to the age of the observable universe = 13.797(23) Gyr (Planck 2018)).

   At time-zero of the Friedmann equation models, we have a(t=0) = 0 which is the big bang singularity.

   In fact, no one (or almost no one) believes we can run the clock on the Friedmann equation models back to time zero.

   But we believe that we may be able to run the clock back to with in a tiny fraction of second of time zero (see Wikipedia: Graphical timeline of the Big Bang).

4. Recall density parameter Ω is the ratio of current universe density to the critical density of the Friedmann equation models.

   Observations circa 2025, Ω ≅ 1 which means the spatial geometry of the observable universe is nearly Euclidean geometry (AKA flat geometry) (see Wikipedia: Λ-CDM model: Parameters).

5. The cosmological constant Lambda (AKA Λ) is the extra general relativity parameter that Albert Einstein (1879--1955) invented to get his static Einstein universe.

   It was dismissed for its original use, but was resurrected to give the accelerating universe.

6. The (Ω=1,Λ=0) model was the favored model before 1998 when the acceleration of the universal expansion was discovered.

   Before circa 1995 (e.g., Scott 2018, p. 10), most people thought the universal expansion must be decelerating (i.e., negatively accelerating) since there was NO reason to think there was a cause for acceleration.

   The (Ω=1,Λ=0) model is the Einstein-de Sitter universe (1932, standard model of cosmology c.1960s--c.1990s) which is NEITHER the Einstein universe (1917) NOR the de Sitter universe (1917).

7. The (Ω=0,Λ=0) model is a zero acceleration model: neither accelerating nor decelerating. This model is usually considered just unrealistic limiting case. However, a version of it does have some have some advocates (see Melia 2014).

8. The (Ω=1,Λ>0) model is an accelerating universe.

   The model originally decelerates and then accelerates.

   The acceleration is starts when a(t) starts curving up rather than down.

   The cosmic time of transition between decelerating and accelerating phases according to the current Λ-CDM model is currently thought to be cosmic time = 7.66(9) Gyr (e.g., Hergt & Scott 2024, p. 6).

   The Λ-CDM model which is the currently favored cosmological model.

   It is fitted to the observations by adjusting 6 independent parameters and gives a good fit to most observations (see Wikipedia: Λ-CDM model: Parameters). However, the Λ-CDM model may need significant revision or even replacement because of the Hubble tension---which we will NOT discuss here---an other tensions.

9. An important test of any viable cosmological model is that it should have an age greater than that of the oldest star.

   Currently, the oldest stars may have ages ∼ 13.6 Gyr (see Wikipedia: List of oldest stars, Roederer et al. 2024; Valcin et al. 2025; Wikipedia: Chronology of the universe: Earliest structures and stars emerge).

   The current Λ-CDM model fitted age of the observable universe = 13.797(23) Gyr (Planck 2018) (see Planck 2018: Age of the observable universe = 13.797(23) Gyr) (see Wikipedia: Age of the universe) which is comfortably older than known oldest stars.