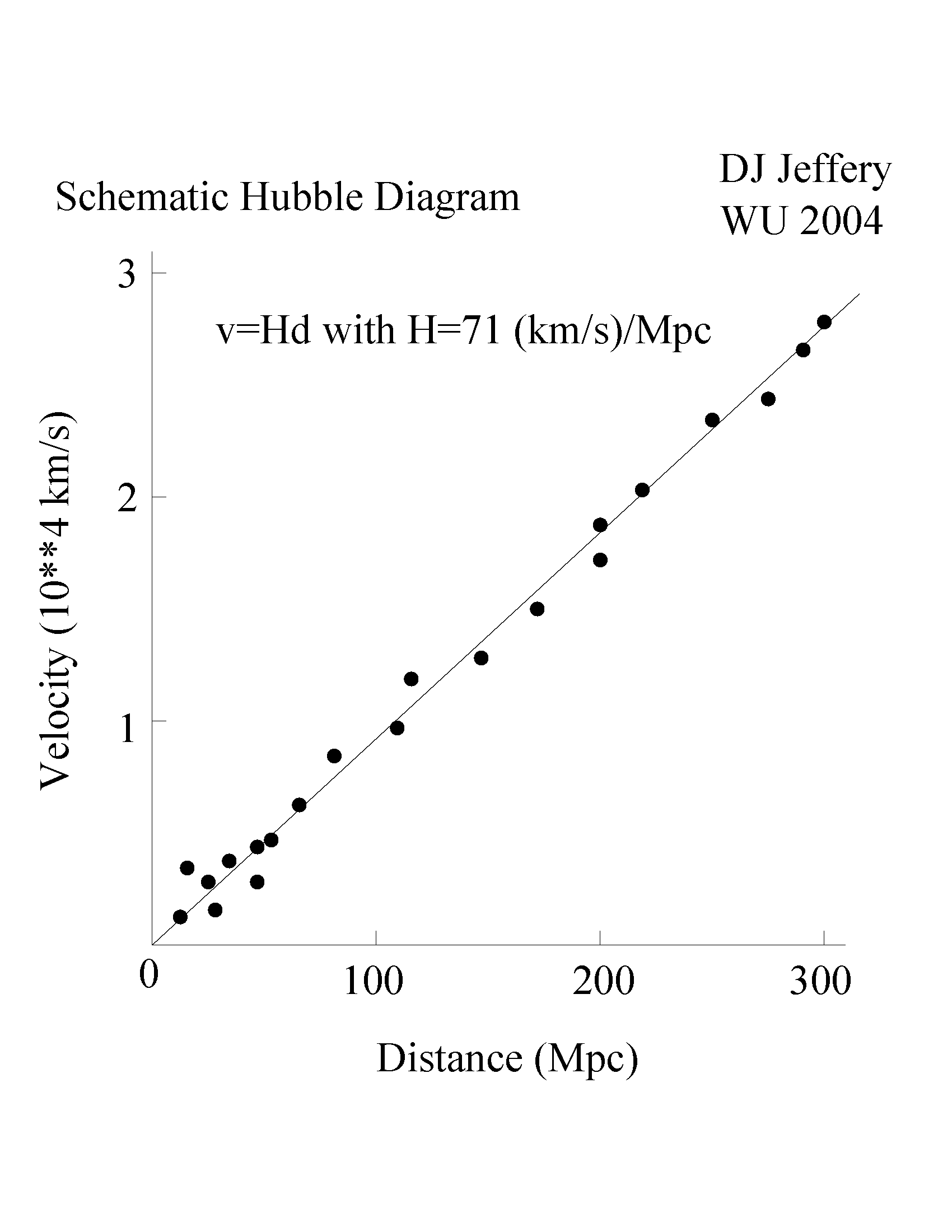
---



Caption: A cartoon Hubble diagram extending out to ∼ 300 Mpc.

For an explication of the Hubble's law, the Hubble constant, and Hubble diagrams, see Cosmology file: hubble_diagram.html.

The theoretical Hubble's law of the FE models is exact for exact recession velocities and cosmological proper distances measured at one instant in cosmic time. The theoretical Hubble's law was derived and first published by Georges Lemaitre (1894--1966) in 1927. It must have been known to Alexander Friedmann (1888--1925) since the early 1920s, but he NEVER explicitly presented it. For more on the discovery of the theoretical Hubble's law, see Astronomer file: georges_lemaitre_cartoon.html.

Now an observational Hubble's law can be determined observationally in a simple way from a Hubble diagram Edwin Hubble (1889--1953) did.

But is that observational Hubble's law actually predicted for the local observable universe? Our physical intuition says yes, but is there a definite proof?

by the theoretical Hubble's law That Hubble's law can be determined empirically is proven using expanding universe models.

The argument is a bit tricky, but here goes.

Luminosity distances (which we discuss below) and angular diameter distances (which we do NOT discuss) are direct observables.

It can be proven that these "distances" asymptotically approach the cosmological physical distance as cosmological redshift z goes to zero. This is illustrated in the cosmological distance measure graphs shown below (where "luminosity is luminosity distance and "angular diameter" is angular diameter distance).

The 1st order recession velocity, given by v_1st=zc, asymptotically approaches the exact recession velocity as cosmological redshift z goes to zero. This is illustrated in the cosmological distance measure graphs shown below since the "naive Hubble" divided by H is the 1st order recession velocity and the cosmological physical distance divided by H is the exact recession velocity.

Since the direct observable "distances" and the 1st order recession velocity approach, respectively, the cosmological physical distance and the exact recession velocity asymptotically as cosmological redshift z goes to zero, they must asymptotically satisfy Hubble's law (which holds exactly for cosmological physical distance and the exact recession velocity) as cosmological redshift z goes to zero.

Thus, as long as one observes cosmological objects at sufficiently small cosmological redshift z, one can find Hubble's law and the Hubble constant empirically from a Hubble diagram.

For the Λ-CDM model as seen in the cosmological distance measure graphs shown below, z must be less than about 0.5 to be sufficiently small.

Credit/Permission: © David Jeffery, 2004 / Own work.
Image link: Itself.
Local file: local link: hubble_diagram_observational.html.
File : Cosmology file: hubble_diagram_observational.html.