General Caption: Big Bang nucleosynthesis (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) is a key element of Big Bang cosmology. The fact that calculated Big Bang nucleosynthesis is in agreement with observation (except to a degree for the cosmological lithium problem) is a key verification of said Big Bang cosmology (see below Image 6 Caption).

The situation is also reciprocal in that other verified elements of Big Bang cosmology lead us to believe calculated Big Bang nucleosynthesis is right. In fact, all well established grand theories or paradigms (as Big Bang cosmology is) are based on a network of mutually supporting verifications which gives them strong credibility.

General Features:
1. The Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) began at ∼ 10 s after the fiducial cosmic time zero (i.e., t=0, lookback time 13.797(23) Gyr (Planck 2018))) of the Friedmann equation (FE) models. At cosmic time ∼ 10 s, the cosmic temperature had fallen sufficiently low that protons and neutrons were NO longer being created by pair creation by photons (since the photons NO have the energy as the required photon energy E=hν as cosmic temperature falls to create such massive particles) and nuclei were NO longer being destroyed by photodisintegration (since the photons NO longer have the photon energy E=hν as the cosmic temperature falls to destroy nuclei). Also by some asymmetry in the early part of early universe (cosmic time (10**(-12) s -- 377700(3200) y), the bulk antimatter had vanished (Wikipedia: Antimatter: Origin and asymmetry; Wikipedia: Baryogenesis). So there was NO longer antimatter to complicate Big Bang nucleosynthesis at cosmic time ∼ 10 s.
2. Big Bang nucleosynthesis is the nucleosynthesis (i.e., creation) of the light elements and isotopes thereof (i.e., hydrogen (H), deuterium (D, H-2), helium-3 (He-3), Helium-4 (He-4), lithium-6 (Li-6) (very little of this), lithium-7 (Li-7)) of the primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7) (which to a large degree is the cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018) composition of the intergalactic medium (IGM) of the observable universe. To be more precise, Big Bang nucleosynthesis produced overwhelmingly most of the modern cosmic abundances of hydrogen, deuterium (of which the nuclei are called deuterons), and helium, and some significant part or maybe almost all of the cosmic abundance of lithium.
  Big Bang nucleosynthesis (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) occurred ∼ 13.8 Gyr ago (see Wikipedia: Age of the universe; age of the observable universe = 13.797(23) Gyr (Planck 2018) (see Planck 2018: Age of the observable universe = 13.797(23) Gyr) as measured from the probably unreal Big Bang singularity which is the fiducial cosmic time zero (i.e., t=0, lookback time 13.797(23) Gyr (Planck 2018))) and, of course, the fiducial time zero of the Λ-CDM model (the current standard model of cosmology (SMC, i.e., the Λ-CDM model)).
3. Just to re-emphasize, Big Bang nucleosynthesis produced overwhelmingly most of the cosmic abundances of hydrogen, deuterons, and helium, and some significant part of the cosmic abundance of lithium-7 and lithium-6. Image 6 below illustrated the yield of these elements.
Image 1 Caption: The nuclear reaction network of Big Bang nucleosynthesis.
For a somewhat more detailed image of the nuclear reaction network of Big Bang nucleosynthesis, see Hyperphysics: Big Bang Nucleosynthesis.
Image 1 Features:
1. For Big Bang nucleosynthesis, the relevant elements, nuclei, isotopes, and particles are the:
  1. gamma ray (γ): a high-energy photon.
  2. neutron (n: free n decays to p, half-life = 610(10)s with uncertainty annoyingly large): a radioactive nuclide (i.e., unstable to spontaeous radioactive decay) when a free particle with half-life 610.(10) seconds = 10.17 minutes. The free neutron decay process is
```
       n → p + e**(-) + ν_(e-bar)  , 
```
    where e**(-) = electron (AKA negative beta particle) and ν**(e-bar) = antielectron neutrino.
  3. proton (p, H): A hydrogen ion (H**(+)): (stable isotope).
  4. deuteron (D or H-2): A stable isotope) which is the atomic nucleus of the species deuterium.
  5. triton (T or H-3: decays to He-3 by beta-minus decay, half-life = 4500(8) days = 12.32(2) Jyr): The atomic nucleus of the species tritium. It is a radioactive isotope with half-life 4500(8) days = 12.32(2) Julian years and radioactive decay product Helium (He-3) (see Wikipedia: Tritium: Decay). The half-life is so long compared to the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) that the triton is effectively a stable isotope relative to the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m). However, all the primordial tritrium obviously decayed away rapidly in cosmic time and it made ∼ 10 % contribution to primoridial Helium (He-3) abundance (see Image 5 below) which is nearly the modern abundance.
  6. helium-3 (He-3): A stable isotope.
  7. helium-4 (He-4): A stable isotope which is much stabler than helium-3 (He-3) which is essentially why it is much more abundant than helium-3 (He-3).
  8. lithium-6 (Li-6): A stable isotope. Li-6 is very minor product of Big Bang nucleosynthesis, and so its reactions are NOT shown in the nuclear reaction network in Image 1. Big Bang nucleosynthesis predicts only ∼ 2/10**5 of lithium (Li) atoms should be Li-6 atoms (see Johnson 2014, "Big Bang ruled out as origin of lithium-6").
  9. lithium-7 (Li-7): A stable isotope.
  10. beryllium-7 (Be-7: decays to Li-7 by electron capture, half-life = 53.22(6) days): A radioactive isotope with half-life 53.22(6) days when it is in UNIONIZED FORM and has radioactive decay product Li-7 (see Wikipedia: Isotopes of Beryllium: Table). In fact, Be-7 radioactively decays by electron capture (p+e(-)→n+μ_e) and this RARELY happens for bare Be-7 nuclei (positive charge +4e). So primordial Be-7 must acquire bound electrons to radioactively decay. Calculations show that the primordial Be-7 radioactively decays to Li-7 (and then adds to the original primordial Li-7 abundance increasing that by a factor of ∼ 10 to the effective primordial Li-7 abundance: see Image 5 below) over cosmic time ∼ 600--1000 years (Cooke 2024, p. 7). The decay time is so long compared to the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) that Be-7 is effectively a stable isotope relative to the Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m).
2. The arrows indicate the nuclear reaction connecting ONE boxed reactant to ONE boxed product with the other reactant/product being the first/second quantity in the brackets: e.g., p(n,γ)D is the same as p + n → D + γ. The n → p is actually n → p + e**(-) + ν_(e-bar). The e**(-) (electron) and ν_(e-bar) (electron antineutrino) are omitted since they just occur as products and do NOT directly affect nuclear reaction network again.
3. There is a key difference between the nuclear reaction network of Big Bang nucleosynthesis and that of stellar nucleosynthesis: in Big Bang nucleosynthesis, there are free neutrons participating in the nuclear reactions.
  Since neutrons are neutral, they have NO Coulomb barrier (i.e., electrostatic force) to overcome to get close enough to other nuclei (which are all electrically charged) in order to undergo a nuclear reaction. The upshot is much faster nucleosynthesis is possible than otherwise such as in hydrogen burning in main-sequence stars. Of course, fast, runaway nuclear burning can happen without free neutrons (e.g., in supernovae), but other special conditions are involved.
4. Based on the website Thespectrum: Big Bang Nucleosynthesis (since yours truly can't find a better source to spit it out right now), the main nucleosynthesis path in the nuclear reaction network (shown in Image 1) is probably
```
          p + n → D        no Coulomb barrier, but D is only weakly stable and so photodisintegration
                                 creates the deuterium bottleneck.
                                 Temperature has to fall low enough to allow deuterium (D, H-2) to
                                 survive long enough for further nuclear reactions.
          D + n → H-3      no Coulomb barrier.
          T + D → He-4     Coulomb barrier,
                                 but the smallest one possible:  just 2 positive
                                 elementary charges
                                 repelling:  i.e., p and p.  
```
  Further nucleosynthesis beyond He-4 CANNOT go by just adding neutrons since the He-4 + n → products and Li-5 + n → products CANNOT survive for further nuclear reactions since He-5 (half-life = 700(30)*10**(-24) s) and Li-5 (half-life = 370(30)*10**(-24) s) are very unstable.
  This bottleneck (beyond the deuterium bottleneck) brings nucleosynthesis to heavier nuclei almost to a stop.
  Just a little lithium-7 (Li-7), lithium-6 (Li-6), and beryllium-7 (Be-7) get synthesized---and the latter radioactively decays away relatively rapidly as discussed above in Image 1 Features.
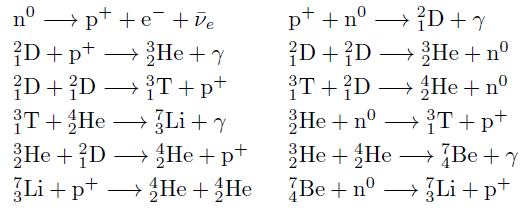
Image 2 Caption: A table of the nuclear reactions important in Big Bang nucleosynthesis. The table is somewhat more complete than the nuclear reaction network displayed in Image 1.
Image 2 Features:
1. A key feature of this table is the reaction that is ABSENT: the proton-proton (p-p) reaction:
```
  p**(+) + p**(+) 
    → D + e**(+) + ν_e + 1.442 MeV  , 
```
  where ν_e is electron neutrino (see Wikipedia: Proton-proton chain reaction: The proton-proton chain reaction). This reaction is many orders of magnitude slower??? than any of the shown nuclear reactions and is negligible in Big Bang nucleosynthesis. The essential reason is that an intermediate step is the formation of He-2 (diproton) which is extremely unstable and causes the overall nuclear reaction to have an extremely small cross section. When He-2 (diproton) does form successfully???, it almost immediately??? undergoes beta plus decay to complete the proton-proton (p-p) reaction. In fact, the weak nuclear force is needed to initiate the reaction and that interaction is much weaker than the strong nuclear force. (Note, the above discussion needs improvement, but that requires an improved reference.???)
2. In the Sun, the time-scale for the proton-proton (p-p) reaction is 7.9*10**9 yr, whereas the p + D → He-3 reaction has time scale 1.4 s (see, e.g., Ian Howarth, 2010, Astrophysical Processes: From Nebulae to Stars, Part 5, Stars II, p. 122). However, proton-proton (p-p) reaction is the initial step---and therefore the rate-determining step---in all 3 branches of the proton-proton chain (PP chain) (i.e., the pp I branch, the pp II branch, and the pp III branch) for energy generation in the Sun. All of stellar evolution is heavily dependent on the proton-proton (p-p) reaction, whereas Big Bang nucleosynthesis NOT at all.
3. Note, the deuterons (D,H-2) in the Sun's core are all produced in the PP chain since primordial deuterons (D,H-2) in the Sun's core were all destroyed very early in the Sun's main sequence lifetime or before by the p + D → He-3 reaction.
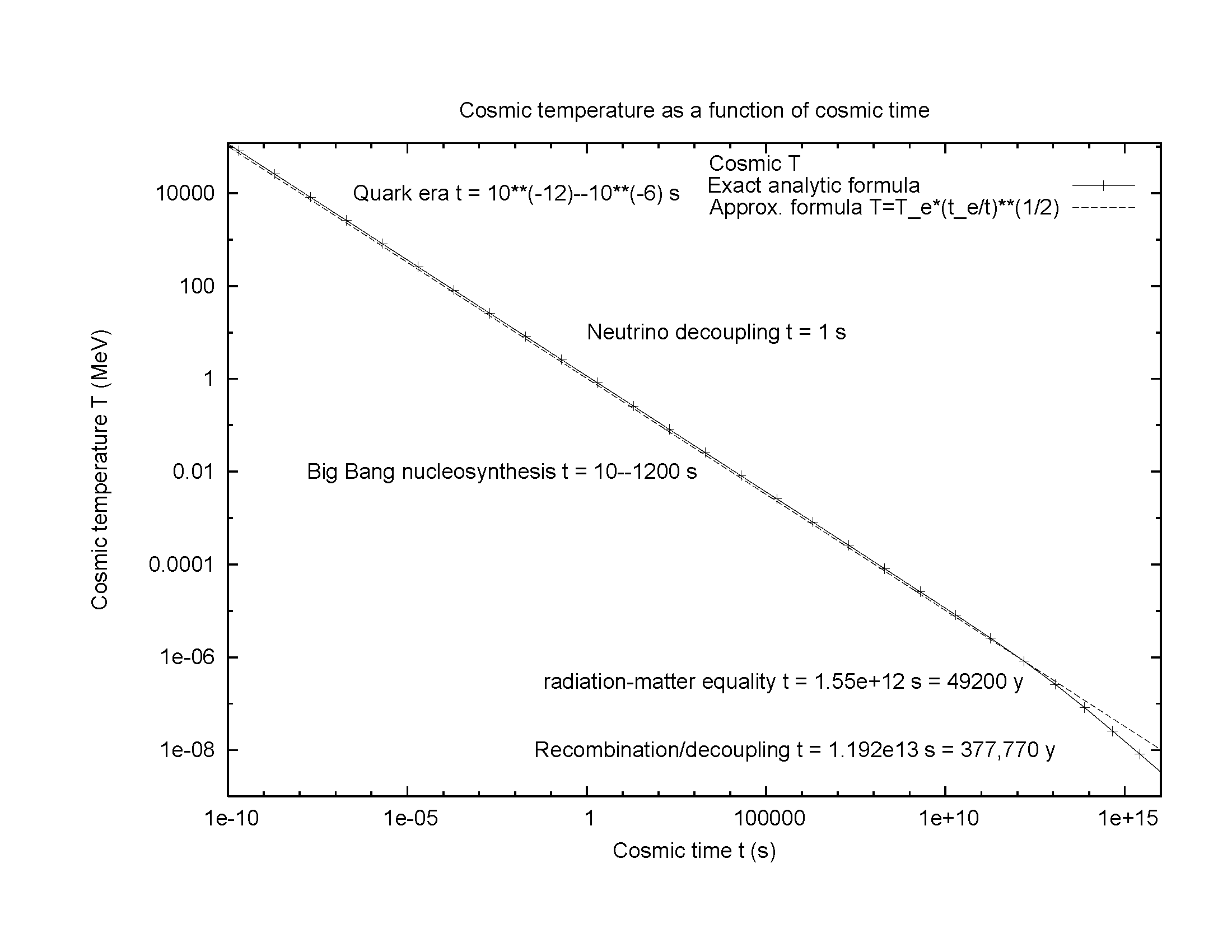
Image 3 Caption: A log-log plot cosmic temperature (in MeV ≅ 10**10 K) versus cosmic time including the time from the quark era (cosmic time t∼ 10**(-12) -- 10**(-6) s) to the recombination era t = 377,770(3200) y ∼ 1.2*10**13 s (when the primordial photons stopped interacting strongly with matter).
Image 3 Features:
1. The fiducial cosmic time zero (i.e., t=0, lookback time 13.797(23) Gyr (Planck 2018))) is the time of the Big Bang singularity which probably did NOT happen. Our best theory is that the inflation era (10**(-36) -- 10**(-32) s) happened in the very early universe (t < 10**(-12) s) and then the observable universe tracked into a standard Friedmann-equation model thereafter.
2. The cosmic temperature is the general temperature of the observable universe. Before the matter decoupling era (cosmic time ∼ 12 Myr ∼ 4*10**14 s) (when matter stopped interacting strongly with the primordial photons) (see Hergt & Scott 2024, p. 6), it was the temperature of all mass-energy of all baryonic matter and primordial photons (i.e., conventionally the CMB even when NOT redshifted to the microwave band: fiducial range 0.1--100 cm) and after that just of the primordial photons. The primordial photons cooled (via the cosmological redshift and the decreasing density of photons both due to the expanding universe) to create the cosmic microwave background (CMB) (in the microwave band (fiducial range 0.1--100 cm, 0.01--10 cm**(-1)) of cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018)
3. The primordial photons have undergone cooling since the quark era at least. Before that we can only extrapolate its behavior.
4. The cosmic temperature is completely dominated by relativistic particles (as far as we know) which means that T ∝ 1/a(t), where a(t) is the cosmic scale factor. The cosmic scale factor scales as t**(1/2) before the radiation-matter equality (cosmic time t∼ 50,000). The radiation-matter equality is the transition time from the radiation era (where the observable universe's mass-energy is dominated by primordial photons) to the matter era (where the observable universe's mass-energy is dominated by matter which includes both baryonic matter and dark matter). After the radiation-matter equality, the cosmic scale factor scales as t**(2/3) thereafter. Thus, T ∼∝ 1/t**(1/2) before the radiation-matter equality (t≅ 50,000) and T ∼∝ 1/t**(2/3). The two behaviors give straight lines on the log-log plot with slopes of, respectively, -1/2 and -2/3.
5. The displayed or present in cosmic eras in Image 3:
  Note again, the fiducial cosmic time zero (i.e., t=0, lookback time 13.797(23) Gyr (Planck 2018))) is the time of the probably unreal Big Bang singularity of the Friedmann equation models. Λ-CDM model. But though probably unreal, it is a fiducial time zero when running backward the clock of cosmic time.
Image 4 Caption: A log-log plot of the cosmic time evolution of Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m).
Image 4 Features:
1. The horizontal axis is logarithmic number density relative to the number density of baryons. Note, the number of baryons is nearly exactly conserved from about baryogenesis era (cosmic time ∼ 10**(-1) s) (see also Wikipedia: Baryogenesis) onward in Big Bang cosmology until the far future maybe.
2. The upper vertical axis is cosmic time measured from the fiducial cosmic time zero (i.e., t=0, lookback time 13.797(23) Gyr (Planck 2018)). The lower vertical axis is cosmic temperature in MeV ≅ 10**10 K for each cosmic time.
3. Keywords for Image 4: baryons, baryon-to-photon ratio η = 6.12(5)*10**(-10) = 273.78(18)*10**(-10)*Ω_b*h**2 (Planck-2018, p. 15, Plik[1]) (see Planck-2018, p. 15, Cooke 2024, p. 7; Wikipedia: Big Bang nucleosynthesis: Characteristics: baryon-to-photon ratio η ≅ 6*10**(-10); Stackexchange: baryon-to-photon ratio), beryllium-7 (Be-7: decays to Li-7, half-life = 53.22(6) days when it is in UNIONIZED FORM) (see Image 1 Features for the ionized lifetime), cosmic temperature, cosmic time (upper axis), deuteron (D or d, H-2), helium-3 (He-3), helium-4 (He-4), hydrogen (H or p), lithium-6 (Li-6), lithium-7 (Li-7), mass fraction (related to number abundance), neutron (n: free n decays to p, half-life = 610(10)s with uncertainty annoyingly large) (see Wikipedia: Free neutron decay: Neutron lifetime puzzle), proton (p, H), triton (T or t,H-3: decays to He-3, half-life = 12.32 Jyr).
4. As illustrated in the Image 4, Big Bang nucleosynthesis essentially spanned cosmic time ∼ 10--1200 s ≅ 0.17--20 m. Then it was all over.
5. The primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7) is the result of Big Bang nucleosynthesis. It consists of just light elements.
  Note, the primordial tritium (T, H-3) and beryllium-7 (Be-7) radioactively decayed away relatively rapidly and conbributed to the modern abundances of, respectively, helium-3 (He-3) and lithium-7 (Li-7). See Image 1 Features for a discussion of these radioactive decays.
6. Note, post-main-sequence stars only contribute a small amount of helium-4 (He-4) to the modern cosmic composition compared to Big Bang nucleosynthesis (BBN).
Image 5 Caption: The key differences between Big Bang nucleosynthesis from stellar nucleosynthesis illustrated.

Image 5 Features:
1. Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m): This is much shorter than the millions of years to billions of years of stellar nucleosynthesis.
2. There is an enormous distinction in that Big Bang nucleosynthesis has free neutrons (as discussed above in Image 4 Features) and stellar nucleosynthesis does NOT.
3. The Big Bang nucleosynthesis temperature is ∼ 10**9 ≅ 0.1 MeV whereas stellar nucleosynthesis has a temperature range ∼ 10**7 to 10**10 K (Google AI question: Stellar nucleosynthesis temperature range?; Wikipedia: Stellar nucleosynthesis).
4. Another difference of Big Bang nucleosynthesis from stellar nucleosynthesis (omitted in Image 5) is that heat energy feedback from the nuclear reactions in Big Bang nucleosynthesis is NOT important in Big Bang nucleosynthesis. The universal expansion of the cosmic photon gas (AKA cosmic background radiation) controls the cosmic background radiation temperature. In stellar nucleosynthesis, the heat energy from nuclear burning is a key ingredient in setting temperature.
Image 6 Caption: "This Schramm diagram depicts the predicted primordial cosmic composition of helium-4 (He-4) (purple line), deuterium (D, H-2) (blue line), helium-3 (He-3) (red line), and lithium-7 (Li-7) (green line), as a function of baryon-to-photon ratio η = 6.12(5)*10**(-10) = 273.78(18)*10**(-10)*Ω_b*h**2 (Planck-2018, p. 15, Plik[1]) (see Planck-2018, p. 15, Cooke 2024, p. 7; Wikipedia: Big Bang nucleosynthesis: Characteristics: baryon-to-photon ratio η ≅ 6*10**(-10); Stackexchange: baryon-to-photon ratio) on the lower horizontal axis and equivalently baryon density parameter Ω_b*h**2 on the upper horizontal axis." (Slightly edited.)
Image 6 Features:
1. The expression Schramm diagram is in honor of David Schramm (1945--1997), one of the pioneers of Big Bang nucleosynthesis (BBN). Yours truly met Dave Schramm long ago.
2. The width of the curves give the 1 standard deviation (1 σ) uncertainty of the Big Bang nucleosynthesis calculation.
3. The heights of yellow rectangles show the observational constraints on the abundances of the primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7). The widths of yellow rectangles just show where the observations are consistent with the calculated curves (including their widths).
4. Note, there is NO constraint for helium-3 (He-3) because it CANNOT be distinguished observationally circa 2025 from the much more abundant helium-4 (He-4) (see Cooke 2024, p. 16). The nuclei of these two species are very different in behavior, but their behavior as atoms in chemistry and spectroscopy are almost identical. And remember, we know what the observable universe is made of principally from spectroscopy.
  But what you say about hydrogen (H) and deuterium (D, H-2) which are also distinct nuclei but nearly identical in their behavior as atoms? It turns out that they are distinct enough as atoms for spectroscopy to tell them apart.
5. The baryon-to-photon ratio η is a free parameter of Big Bang nucleosynthesis (BBN) calculations.
  But the baryon-to-photon ratio η = 6.12(5)*10**(-10) = 273.78(18)*10**(-10)*Ω_b*h**2 (Planck-2018, p. 15, Plik[1]) (see Planck-2018, p. 15, Cooke 2024, p. 7; Wikipedia: Big Bang nucleosynthesis: Characteristics: baryon-to-photon ratio η ≅ 6*10**(-10); Stackexchange: baryon-to-photon ratio) is fixed by observations of cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009)) (see (Spergel 2003, p. 11).
  Thus, Λ-CDM model and all the observations that are used to fit it, Big Bang nucleosynthesis (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) has NO free parameters.
6. The photon abundance in Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) since that is almost constant from that time to cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018). The photons in question are NOT all photons, but just those in the cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009)) whose abundance we can directly measure. Why is the CMB photon abundance conserved to high accuracy? The short answer is the conditions of the observable universe and thermodynamics require it.
  However, we do NOT know the baryon abundance to high accuracy/precision from measurements of the local observable universe.
  The upshot is that the high accuracy/precision determination of baryon-to-photon ratio must depend on the cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009)) (see (Spergel 2003, p. 11).
7. The fit to observations of free parameter free Big Bang nucleosynthesis (BBN) is considered excellent overall as seen in Image 6
  1. The Helium-4 (He-4) fit is good.
  2. The deuterium (D,H-2) fit is amazingly good.
  3. There is NO fit for helium-3 (He-3) as of circa 2025 for reasons as discussed above.
  4. The lithium-7 (Li-7) observed in certain low metallicity main-sequence stars has been considered the best observational abundance for primordial Li-7. However, as Image 6 shows, this observational abundance is ∼ 1/3 of the prediciton of BBN (Wikipedia: Cosmological lithium problem: Observed abundance of lithium). The discrepancy, called the cosmological lithium problem, is a significant concern for BBN. However, circa 2025 is thought likely that unaccounted-for lithium burning in stellar nucleosynthesis occurs in the observed low metallicity main-sequence stars is the cause of the discrepancy and NOT BBN (Cooke 2024, p. 20). A key point is that despite the discrepancy, the agreement is between observation and prediction is still order of magnitude good.
  Overall conclusion for primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7) is that there is excellent agreement over 8 orders of magnitude between observations and BBN. Thus, there is strong evidence that we understand BBN and thus, BBN is very strong evidence for Big Bang cosmology. The evidence also supports the conclusion that Λ-CDM model (which is the usual assumption of BBN) is at least a good overall description of the observable universe even if it turns out to NOT be the true version of Big Bang cosmology.
8. Now the strong evidence for BBN gives strong faith in the determined baryon abundance.
  However, this means that dark matter CANNOT be baryonic matter. In fact, the baryon fraction (ratio of baryonic matter to baryonic matter plus dark matter) is ∼ 1/6 = 16 % for observable universe (Ci-27) as we know from galaxy rotation curves and other evidence (see Galaxies file: galaxy_rotation.html; Galaxies file: galaxy_rotation_curve_cartoon.html).
  Besides being ruled out as baryonic matter by BBN, dark matter is also ruled out nearly by being very, very dark. It is believed that if dark matter was baryonic matter AND as abundant as it is, then it would emit electromagnetic radiation (EMR) that is obviously coming from baryonic matter. Many theories predict dark matter does produce some EMR, but NOT nearly as much as the same amount of baryonic matter.
9. To complement Image 6, the predictions of primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7) from Big Bang nucleosynthesis are compared to observations below in Table: Big Bang Nucleosynthesis (BBN) Predictions and Observed Primordial Cosmic Composition.
```
Table:  Big Bang Nucleosynthesis (BBN) Predictions and Observed Primordial Cosmic Composition
_____________________________________________________________________________

Element        BBN           Observed           Quantity
_____________________________________________________________________________
He-4           0.2485(20)    0.2453(34)         mass fraction
D (H-2)        2.692(177)    2.527(3)           D/H, x*10**(-5)
He-3           9.441(511)    ≥ 11(2)            He-3/H, x*10**(-6)
Li-7           4.283(335)    1.58(35)           Li-7/H, x*10**(-10)
_____________________________________________________________________________ 
```
  Notes:
  1. The values are from Bertulani et al. 2022, p. 5. Note, these values are representative. Different research groups are always producing slightly updated, slightly different values.
  2. The "elements" (i.e., species) in the table are deuterium (D, H-2), Helium (He-3), helium-4 (He-4), and lithium-7 (Li-7).
  3. Helium (He-3) and helium-4 (He-4) CANNOT easily be distinguished observationally as they are chemically and spectroscopically nearly identical since they are both isotopes of helium (He). So the lower limit on the cosmic He-3 abundance given in the table is probably very uncertain.
The Anthropic Principle Aspect:
There is an anthropic principle aspect of Big Bang nucleosynthesis (BBN).
If the strong nuclear force were just a bit stronger than it is, the Big Bang would have nuclearly burned all the hydrogen into helium (see Wikipedia: Anthropic principle: Anthropic observations: scroll to the 3rd paragraph).
Without hydrogen, there would be NO water and NO hydrocarbons, and therefore would be NO life as we know it.
Life as we know it uses liquid water as the medium for all its chemical reactions and there is NO substitute that we think likely.
Also long-lived stars are probably needed for life as we know it and probably could NOT exist without forming as mainly hydrogen.
The upshot is that the existence of hydrogen constrains the strong nuclear force to be NOT much stronger than it is.
This upshot leads to an anthropic principle argument for the multiverse paradigm since there is NO known fundamental (and human-independent) reason making the strong nuclear force just as strong as it is. With NO known fundamental (and human-independent) reason, it seems plausible that the strong nuclear force strength is somehow randomly chosen. But if the strength is randomly chosen, there is some distribution of strengths and all of these strengths could be chosen elsewhere. Elsewhere could be different pocket universes in a multiverse (which may be an eternal inflation universe) and its strength in our pocket universe is below the upper bound needed for hydrogen to exist since entities needing hydrogen are in our pocket universe. So a multiverse is somewhat plausible. However, remember that all anthropic principle arguments it seems lead to endless disputes about their validity.

Images:

Credit/Permission: © User:Pamputt, 2019 / CC BY-SA 4.0.
Image link: Wikimedia Commons: File:Main_nuclear_reaction_chains_for_Big_Bang_nucleosynthesis.svg.
Credit/Permission: User:Cmbant, 2011 / Public domain.
Image link: Wikimedia Commons: File:Primordial_nucleosynthesis2.png.
Credit/Permission: © David Jeffery, 2019 / Own work.
Image link: Itself.
Credit/Permission: © Chris Mihos, before or circa 2016 / None.
Image link: nucleosynth_fig.jpg.
Image link: Placeholder image alien_click_to_see_image.html.
The Li-6 in nucleosynth_fig.jpg looks way too high since accurate Big Bang nucleosynthesis predicts only ∼ 2/10**5 of lithium (Li) atoms should be Li-6 atoms (see Johnson 2014, " Big Bang ruled out as origin of lithium-6"). Creators of this particular Big Bang nucleosynthesis plot may have articifially increased the cross section of Li-6 to match the observed abundance in modern observable universe. The discrepancy between the Li-6 abundance from (accurate) Big Bang nucleosynthesis of observed abundance is part of the cosmological lithium problem which we discussed above.
Credit/Permission: © Tsung-Han Yeh, Keith A. Olive (1956--), Brian D. Fields 2023 (uploaded to Wikimedia Commons by User:Pamputt, 2023) / Creative Commons CC BY-SA 4.0.
Image link: Wikimedia Commons: File:Universe-09-00183-g004.png.
See also Credit/Permission: © Chris Mihos, before or circa 2016 / None.
Image link: nucleosynth_fig.jpg.
Credit/Permission: © David Jeffery, 2023 / Own work.
Image link: Itself.
Former image: Credit/Permission: © Ann Zabludoff???, before or circa 2012 / None. The now dead link Atropos: Primordial Nucleosynthesis versus Stellar Nucleosynthesis is very enlightening, but it completely omits the enormous distinction that Big Bang nucleosynthesis has free neutrons (as discussed above) and stellar nucleosynthesis does NOT.
Credit/Permission: © User:Paleo2, 2020 / CC BY-SA 4.0.
Image link: Wikimedia Commons: File:Schramm plot BBN review 2019.png.

local link: big_bang_nucleosynthesis.html

Cosmology file

big_bang_nucleosynthesis.html