- Introduction
-
This lecture
(IAL 2: The Sky)
and the next 2 lectures
(IAL 3: The Moon: Orbit, Phases, Eclipses
and IAL 4: The History of Astronomy to Newton)
consist mostly of old astronomy.
So astronomy mostly from before 1900 and some of it from long before going back millennia.
Old astronomy is mostly the astronomy of what we see in the sky---the astronomical sky which is mostly above the Earth's atmosphere---the exceptions are objects in low Earth orbits which are NOT entirely above the Earth's atmosphere.
Old astronomy does NOT concern itself with the internal structure of the astronomical objects.
Old astronomy is still needed for modern astronomy---and so we still need to know it---but the astrology bits are just for fun: see the zodiac figure above and the figure possibly of Cleopatra (69--30 BCE) below (local link / general link: cleopatra.html).
Modern astronomy as the main focus starts from IAL 5: Physics, Gravity, Orbits, Thermodynamics, Tides and goes on and on.

Caption: "The 1st century BCE Denderah Zodiac (19th-century engraving)".
The zodiac was probably been formulated in the first half of the 1st millennium BCE by Babylonian astronomers.
Yours truly is NOT sure he can recognize any zodiac constellations unambiguously. The artists may have been more interested in decoration than astronomy. Well, maybe Pisces and Taurus are there. Holding up the zodiac seems to be Egyptian gods Horus (with the falcon head) and maybe Isis.
Cleopatra could have explained it all to us.
Credit/Permisson: ancient Egyptian artist, 50 BCE as known from the embedded astronomical positions, and thus actually from the late Ptolemaic Kingdom---the reign of Cleopatra (69--30 BCE), in fact---(uploaded to by User:Jic, 2005) / Public domain.
Image link: Wikipedia: File:Dendera.jpg.
- Parallax
-
When we look up at the SKY---beyond the clouds that is---it is
all very REMOTE.
- What Is Parallax?
-
Question: What is
parallax?
- A quick zigzag motion of astro-bodies.
- The change in the angular positions of objects as the observer moves.
- An over-the-counter medication for constipation.
Answer 2 is right.Answer 3? You're thinking of ex-lax.
Ergo, the astro-bodies are very remote compared to the size of the Earth.
Recall that the Sun and planets are of order a few or a few tens of astronomical units away.
The Moon is much closer at about 60 Earth radii away, but to crude measurements it show NO parallax either.
The nearest stars are of order a few parsecs away. One needs really precise measurements to detect their parallaxes.
- Parallax Measurements:
Parallax measurements can be used to determine distance by simple geometry: to be specific trigonometry.
You need to measure the baseline between two angular measurements that are used to determine parallax.
The larger the baseline, the larger the parallax and, usually, the more accurate the measurement.
If the baseline is too small, parallax, and therefore distance, CANNOT be measured at all.
How baseline and parallax are used to obtain distances is illustrated in the figure below (local link / general link: right_triangle.html).
- The Earth Equatorial Radius Baseline and the Fixed Stars:
The rotation of the Earth on the Earth's axis gives a largish baseline by moving an observer by a distance up to 2 Earth equatorial radii (with R_eq_⊕ = 6378.1370 km).
But that baseline is still too small to see the parallax of Solar System objects relative to the observable universe (or, too good approximation usually, the fixed stars) without fairly advanced techniques.
See the explication of the fixed stars in the figure below (local link / general link: ptolemy_muse.html).
- Stellar Parallax and the Parsec:
The revolution of the Earth around the Sun gives a much larger baseline for parallax measurements than any baseline just on the Earth: up to 2 Earth orbit radii: i.e., up to 2 astronomical units.
However, it is the baseline of 1 astronomical unit that leads to the distance unit the parsec (pc).
The figure below (local link / general link: parallax_stellar.html) shows how stellar parallax is determined and how the parsec is defined.
- EOF
- Distance Measurements Are Tough, Especially for the Ancients:
A 2-AU baseline is NOT a large enough baseline for simple methods to detect parallax of even the nearest stars against the background of remote stars.
-
A stellar parallax
determination (by advanced for the day methods) was first made in
1838 by
Friedrich Bessel (1784--1846)
(see file
friedrich_bessel.html).
However, Isaac Newton (1643--1727)
himself had made the first
order-of-magnitude
accurate distance measurement to
a star
(Sirius)
in 1685, but the result was
NOT published until 1728
(see No-374).
However again, Newton did NOT
use stellar parallax, but
what we would now call a
luminosity distance measurement.
There are complications. The Solar System objects are actually moving in the center-of-mass (CM) inertial frame of the Solar System (which is approximately the location of the Sun, but NOT always inside the Sun) on time scales of the revolution of the Earth: i.e., on the time scale of a year.
-
Recall, inertial frames
are discussed in detail in Mechanics file:
frame_basics.html.
So it's hard to disentangle parallax effects from other motion effects for Solar System objects---and for the Ancients to even recognize that there were parallax effects.
The upshot of this discussion is that from simple observations, we CANNOT know the distances to the astro-bodies.
We have the procedures nowadays to get good distances.
But those were NOT available to the Ancients who had to largely guess at distances or give up trying to know them. The later ancient Greek astronomers finally got a fairly accurate distance to the Moon of ∼ 60 Earth radii (No-102). But beyond the Moon, the Ancients had NO accurate distances.
It is true to say that accurate distances are always harder to measure then accurate angular positions in whatever age you are living in.
And you know it is REMOTE because the astro-bodies to the naked eye---or even the contact-lens-coated eye---and even to simple instruments show NO parallax.
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 2 problems 2--9 on parallax and the celestial sphere.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 2.
- The Celestial Sphere
-
What of the old celestial sphere?
- The Dome of the Sky
- The Round Earth and Celestial Sphere of the Stars
- The Modern Celestial Sphere
- Celestial Sphere Basics
- Complications with Using the Celestial Sphere
- Best Celestial Sphere Video Ever!!!
- The Circumpolar Sky
- More Illustrations of Circumpolar Behavior
- What Are the Atltitudes of the NCP and SCP?
- The Dome of the Sky:
If you just stay in one region of the Earth, the astro-bodies could be located on a big dome of the sky over the flat Earth.
The astro-bodies can be seen as traveling over this dome of the sky every day with the Sun, Moon, and planets executing more complicated motions superimposed motions relative to the fixed stars. See the explication of the fixed stars in the figure above (local link / general link: ptolemy_muse.html).
Without measurable parallaxes or other distance indicators for the astro-bodies, how could you tell that this dome model it was NOT true.
Perhaps the ancient Sumerians and Babylonians, who never got out of the Tigris-Euphrates River area, perceived the sky this way---we don't know--they didn't tell us---they may have had various ideas.
For a possible Babylonian cosmology, see the figure below (local link / general link: babylonian_cosmos.html).
- The Round Earth and Celestial Sphere of the Stars:
So the Babylonian astronomers and Babylonians in general probably thought the Earth as a flat Earth.
-
Question: But what if you had sailed with
Ferdinand Magellan (1480--1521)
(see the figure below:
(local link /
general link: magellan_earth.html)
and knew the world was round and everywhere you
went---Lisbon,
Tierra del Fuego,
the Philippines,
Africa ...
Then you might guess that the sky was a giant remote:
There is no absolutely right answer, but yours truly would say answer 3.If you can't tell distances to astro-bodies, you can't say anything for sure about the geometry of the astro-bodies in 3-dimensional space.
But the simplest picture is that the astro-bodies are located on a big sphere that surrounds the Earth.
If they were located on some other kind of shape, one would expect asymmetries in the distribution of stars: e.g., a clustering of stars at the corners of a tetrahedron where there is more surface area per solid angle than elsewhere on the tetrahedron.
With the astro-bodies located on a sphere, one could easily imagine that the astro-bodies would travel around on the sphere daily.
It is even more easy to believe that they are carried by the sphere as it spins around daily.
Even if you believe in a flat Earth---and some claim to do so to this day---you could still believe in the giant remote sphere revolving around the a tiny flat Earth on plane near the center of the sphere. The sphere revolves aroung the flat Earth once per day.
But you can't believe in a flat Earth if were one of Magellan's crew.
We call this big sphere, following ancient tradition, the celestial sphere.
No simple observation contradicts this celestial sphere theory as a real model of the cosmos.
The celestial sphere theory even makes philosophical sense if you know the Earth is ROUND and believe it is at the center of the cosmos. One could reason that the cosmos has spherical symmetry everywhere.
The ancient Greeks did come to believe in the spherical Earth theory from the 5th century BCE and that theory got passed on as truth in western Eurasia to later Classical Antiquity, the Medieval Islamic world, Medieval Europe, and Renaissance Europe. See the discussion in the figure below (local link / general link: parmenides_earth.html).
This theory was part of Aristotelian cosmology which was a geocentric cosmology with a spherical Earth. It had the fixed stars located on a rotating physical celestial sphere---the celestial sphere of the stars.
For Aristotle (384--322 BCE), the "supreme authority", see the figure below local link / general link: aristotle_supreme.html).
A key reason is that the ancient Greek astronomers (see subsection Distance Measurements Are Tough, Especially for the Ancients above) and their successors up to 17th century could NOT measure astronomical distances very well.
In fact, ancient Greek astronomers did try to measure astronomical distances, but the only success was that they did eventually figure out that the Moon distance was ∼ 60 Earth radii: see the figure below (local link / general link: aristarchos_manuscript.html).
Their geometry was strong, but their instruments were weak.
The parallaxes of all the astro-bodies beyond the Moon were just too small for techniques from before the 17th century to measure.
Now the Magellan-Elcano circumnavigation tended to confirm Aristotelian cosmology---the Earth was round just like Aristotle said it was---but later work by Nicolaus Copernicus (1473--1543), Galileo Galilei (1564--1642), Johannes Kepler (1571--1630), Isaac Newton (1643--1727), and others, relegated Aristotelian cosmology to history.
The celestial sphere of the stars disappeared as a physical object and became imaginary, infinitely remote celestial sphere on which all astro-bodies are projected for the purposes of location.
- The Modern Celestial Sphere:
Nowadays, the celestial sphere is NOT a physical body anymore, of course.
It is an imaginary sphere quasi-infinitely beyond any physical astro-body.
The actual astro-bodies are viewed as projected onto the celestial sphere for location purposes. We discuss locating astro-bodies on the celestial sphere below in section Location on the Sky and Coordinate Sytems.
Some first points about the celestial sphere:
- The whole celestial sphere revolves
around the Earth once per day as seen from
the Earth, of course.
Actually, once per sidereal day. We'll discuss sidereal day below in section The Sun on the Celestial Sphere.
- Physically, we think of the Earth
as rotating on its
axis
(as in the animation below)
and NOT of the surrounding
universe rotating about us.
- But either perspective is a valid geometrical description of motion.
For a discussion, see the figure below
(local link /
general link: /celestial_sphere_rotating.html).
- In fact, for most astronomical observational purposes and in often in everyday life, we take the Earth as being at rest and the surrounding universe as rotating about us.
This is a geocentric perspective---which is a very humankind egocentric perspective.
- Why then do we say the Earth is "rotating physically"?
Earth is rotating relative to fundamentally absolutely unrotating observable universe with respect to which all inertial frames do NOT rotate---except maybe in very strong gravitational fields like near black holes???---but yours truly has to guess about this since no one explicates this factoid. The best explication so far (and it does NOT say much) is Wikipedia: Inertial frame of reference: General relativity.
-
In old astro jargon,
one says that the Earth
is rotating relative to the
fixed stars.
But this is now known to be only approximately true since
the fixed stars
(just the relatively nearby stars
that you see in the night sky)
do rotate slowly with respect to the
observable universe.
So using the phrase "relative to
the fixed stars" should
discontinued since the fixed stars
only approximate the unrotating frame of the
observable universe.
All this explanation is too long to say everytime we need to say it.
So as a shorthand, we say that the Earth "physically" rotates and the observable universe does NOT "physically" rotate.
However, we can say either geometrically rotates relative to the other depending on our descriptive needs.
- As well as the overall daily motion of the astro-bodies by being carried around by the rotating celestial sphere, the astro-bodies also have motions relative to the celestial sphere.
The motions are easily observed for astronomical objects in the Solar System since these motions are relatively rapid. We will discuss these motions below (see sections The Sun on the Celestial Sphere and The Moon, Planets, Asteroids, and Comets on the Celestial Sphere).
Extrasolar objects (i.e., astronomical objects outside of the Solar System) also move relative to the celestial sphere, but this motion becomes harder to detect in direct way as the extrasolar objects get farther away since the angular extent of the motions on the sky strongly tends to get smaller with increasing distance.
- Why do the angular motions relative to the celestial sphere strongly tend to get smaller with increasing distance?
Velocities relative to local inertial frames for most observable astro-bodies are of order a few hundred kilometers per second and the biggest ones are of order a few tens of thousands of kilometers per second.
At distances of kiloparsecs and megaparsecs, the distances traveled by astro-bodies on human time scales at such velocities are minute compared to the distances to the astro-bodies.
Now angle is ratio of the projected length of an object divided by the distance to it aside from some conversion factor if you are NOT using radian measure.
So at distances of kiloparsecs and megaparsecs, the angular motions are minute on human time scales.
Our ability to directly detect these motions is improving, but it is still limited to stars and other astro-bodies in our neighborhood of the Milky Way.
Indirectly, we can detect radial motions (i.e., line of sight motions, NOT angular motions) far away via the Doppler effect (see IAL 7: Spectra) and the cosmological redshift z (see IAL 26: The Discovery of Galaxies and IAL 30: Cosmology).
- In fact, for most astronomical observational purposes and in often in everyday life, we take the Earth as being at rest and the surrounding universe as rotating about us.
- Celestial Sphere Basics:
The basic idea of the celestial sphere is illustrated in the figure below (local link / general link: celestial_sphere_000_basic_idea.html).
-
Of course, there really is
parallax
if you use
very refined techniques, but even most professional
astronomy doesn't have to worry about that
parallax too much.
- Points and Circles on the Celestial Sphere:
There are special points and circles that we put on the celestial sphere.
These points and circles help with finding astro-bodies on the celestial sphere and understanding and tracing their motion.
The figure below (local link / general link: celestial_sphere_001_features.html) explicates the some of the basic of the special points and circles.
- A Bit More on Polaris:
Just a bit more about Polaris, the pole star of our historical period.
Polaris (α UMi) (or the Pole Star or the North Star) is 44'09'' (44 arcminutes, 9 arcseconds) from the NCP in year 2000 coordinates (more precisely J2000.0 coordinates).
So it's less than a degree from NCP---which is which is about or less than a finger width at arms length (Hand Angle Measurements).
Polaris is a moderately bright star (visual magnitude of 2.02), and thus can be used to identify the NCP (which is just an empty point on celestial sphere).
Polaris is the end star of the handle of the Little Dipper---which is an asterism (i.e., a non-official constellation)---is part of the modern standard constellation Ursa Minor.
But the Little Dipper is NOT a particularly obvious asterism and NOT the give the easiest way finding of Polaris.
The easiest ways of finding Polaris are illustrated in the figure below (local link / general link: polaris_ursa_minor_major.html).
- The Celestial Sphere Rotates Westward Relative to the Fixed Earth:
Now the Earth rotates eastward relative to the observable universe, but if you take the fixed Earth as your frame of reference, the whole celestial sphere rotates west.
But you can only see what is above your local horizon which is the great circle that cuts the celestial sphere in half: above the sky, below the ground.
So what we usually see: astro-bodies rising east and setting west on the horizon as the sky turns.
Artificial satellites in low earth orbit can rise and set anywhere if their angular velocity relative to the fixed stars is fast enough.
This point is illustrated in the figure below (local link / general link: gps_global_positioning_system.html).
Insofar as they are approximated as unmoving on the celestial sphere, astro-bodies are carried around daily on the celestial sphere on circles parallel to the celestial equator.
-
Except for those astro-bodies on the
celestial equator itself, the
circles are small circles.
Small circles are circles on spheres that DO NOT cut the spheres in half.
Those astro-bodies on the celestial equator have great circle paths.
Great circle are circles on spheres that DO cut the spheres in half.
- A Bit More on Polaris:
- Complications with Using the Celestial Sphere:
There are TWO COMPLICATIONS in seeing the circling of the astro-bodies with the celestial sphere:
- Bright daylight and clouds usually
totally hide astronomical objects.
Note especially, most
astronomical objects are too dim
to be seen against the
diffuse sky radiation
(i.e., the blue sky)
caused sunlight
scattering in the
Earth's atmosphere.
- The
celestial sphere
is cut in half at an oblique angle by the
horizon of the Earth.
The Earth is round, but to a little human anywhere on the Earth, the Earth seems like an infinite flattish plane.
Understanding the astronomical sky would be much easier for us little humans if the Earth didn't block our view.
For an illustration of this problem, see the figure below (local link / general link: celestial_sphere_002_horizon.html).
- Best Celestial Sphere Video Ever!!!:
See celestial sphere | 1:45: Best celestial sphere video ever!!! below (local link / general link: celestial_sphere_videos.html). It makes the celestial sphere idea very clear.
- The Circumpolar Sky:
The circumpolar sky is explicated in the figure above (local link / general link: celestial_sphere_005_circumpolar.html).
- More Illustrations of Circumpolar Behavior:
A simple case for circumpolar objects is that of an observer at the North Pole or the South Pole. He/she would see one hemisphere of the celestial sphere spin around every day with all star paths parallel to the horizon---all stars are circumpolar stars for this observer.
The figure below illustrates this case.
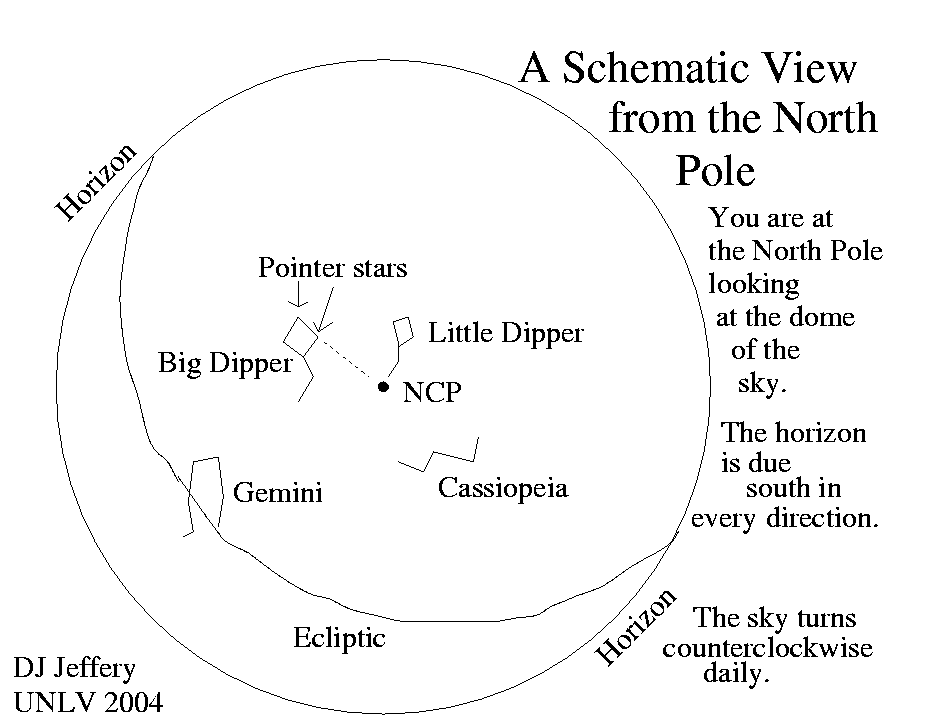
Caption: The cartoon sky map shows sky from the North Pole.
The NCP, zenith, and approximately Polaris all coincide.
-
Zenith is the point on the sky
directly above the observation point.
Nadir is the opposite point on the sky which you usually can't see since you-know-what is in the way.
The edge of the sky map is at the observer's horizon which for this location is the celestial equator itself.
A few constellations are shown in outline approximately: the Little Dipper, the Big Dipper, and the pointer stars, Cassiopeia, and Gemini.
The curve across the sky is the ecliptic which we will discuss below in subsection The Ecliptic. It is the path of the Sun on the sky.
The rotation of the celestial spheres is westward which means that it is counterclockwise looking up when at the North Pole.
Just imagine looking south from where you are and seeing the westward rotation. Now imagine backing up northward to North Pole and it's clear the rotation is counterclockwise about the zenith.
Credit/Permission: © David Jeffery, 2004 / Own work. Image link: Itself.
If you are NOT at the North Pole/South Pole, the NCP/SCP is NOT at zenith and the stars do NOT move in circles around zenith.
They still move in circles around the celestial axis, of course.
In the Northern Hemisphere looking to the north, the NCP is above the horizon and you see the stars circling it. Those stars sufficiently close to the NCP that they don't pass below the horizon are circumpolar as aforesaid.
We show a diagram of their motion in the figure below.
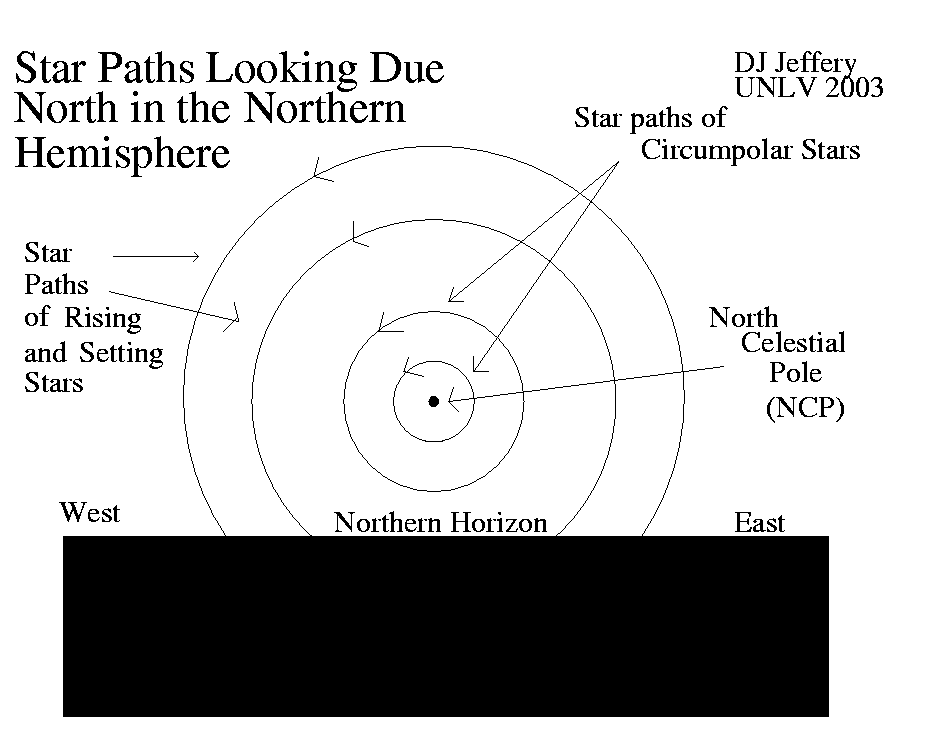
Caption: Star paths looking north.
The observer is in the Northern Hemisphere at mid-latitudes.
Credit/Permission: © David Jeffery, 2003 / Own work. Image link: Itself.
In the Northern Hemisphere looking to the south, the SCP is below the horizon.
Stars south of the NCP by an angle equal to its altitude (which is equal to its latitude) will NOT be NCP circumpolar stars.
They must rise and set OR always be below the horizon: i.e., those sufficiently close to the SCP to be SCP circumpolar stars. See the figure below.
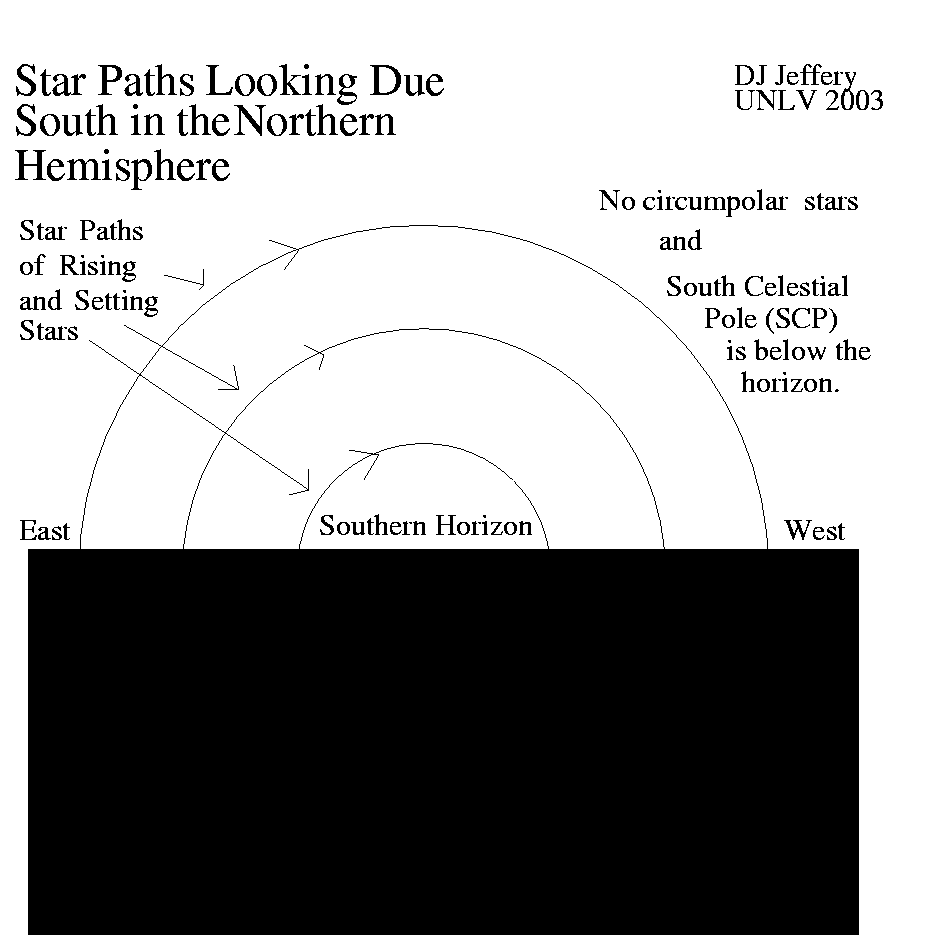
Caption: Star paths looking south.
The south celestial pole (SCP) is just barely below the horizon which means the observer is just barely north of the equator.
Credit/Permission: © David Jeffery, 2003 / Own work. Image link: Itself.
In the figure below (local link / general link: sky_swirl_polaris_animation.html), we show an animation of the NCP circumpolar stars.
- What Are the Atltitudes of the NCP and SCP?
First, we need to say that altitude in astronomy is the angle to an astronomical object measured straight up from the horizon toward zenith.
Now what are the altitudes of the NCP and SCP for any latitude L?
The altitude of the NCP from due north and the altitude of the SCP from due south are, respectively,
AN_NCP = L and AS_SCP = -L ,
where L is latitude and, recall, southern latitude are measured as negative. The formulae are proven in Celestial sphere file: celestial_sphere_005_circumpolar.html: Image 2. SHOW this image in class.-
Question: What is the altitude of the
NCP
above due north
in Moscow, Idaho?
HINT: You should be able to deduce the answer.
- 0°.
- 36°.
- 47°.
- 49°.
- 66.6°.
- 90°.
Answer 3 is right.Moscow is located at 46° 43 arcminutes 54 arcseconds north latitude.
Answer 1: you are on the equator.
Answer 2: you are in Las Vegas, Nevada.
Answer 4: you are on the US-Canada border. You know: the 49th parallel.
Answer 5: you are at the North Pole.-
Question: Since Las Vegas is about 36° north, how many
spread hands at arm's length is the
NCP
above the horizon?
HINT: You should be able to deduce the answer.
- About one half.
- About 1.
- About 2.
- About 4.
Answer 2 is right.A spread hand is about 20° (Hand Angle Measurements).
- The Round Earth and Celestial Sphere of the Stars:
-
Subsections:
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 2 problems 2--9 on parallax and the celestial sphere.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 2.
- Location on the Sky and Coordinate Systems
-
The astro-bodies can be located on the
celestial sphere
in several different ways.
- Constellations as Skymarks:
A crude, but easily remembered, and highly useful way of locating an astro-body on the celestial sphere is to locate it by what constellation it is in. In modern astronomer jargon, a constellation is NOT a set of stars, but a defined region on the celestial sphere that contains the set of stars making up the historical constellation.
These constellation regions tile the whole celestial sphere without overlap, and so provide an unambiguous means of locating astro-bodies on the celestial sphere.
One can say, for example, that the Sun is in Aquarius about March 1 (Se-21) and in Pisces on Mar21 (approximately the vernal equinox). See the figure below (local link / general link: iau_pisces.html).
Locating astronomical object by constellation is useful for rough work and contemplation by both by amateur and professsional astronomers since some of us know the celestial sphere pretty well and the constellations are SKYMARKS.
Actually, amateur astronomers are probably better at this than professional astronomers---who are sometimes profoundly ignorant of constellations as SKYMARKS.
We will look at constellations in section Constellations and the sections following that one.
- The Horizontal Coordinate System:
A second way locating astro-bodies on celestial sphere is by using horizontal coordinates (AKA local coordinates).
Horizontal coordinates are good for locating astro-bodies at one instant in time at one place on the Earth.
They make use of markers and directions that are easily understood by humans without much in the way of elaborate measuring instruments.
But every astro-body's horizontal coordinates change rapidly with time as the Earth rotates and at any one time are different for different points on Earth.
So horizontal coordinates are NOT good for catalogs or other long-term records.
The horizontal coordinates are explained in the figure below (local link / general link: horizontal_coordinates.html).
The meridian is a great circle on the celestial sphere that passes from due north on your horizon through your zenith and then to due south on your horizon.
When an astro-body crosses meridian that is called transiting the meridian.
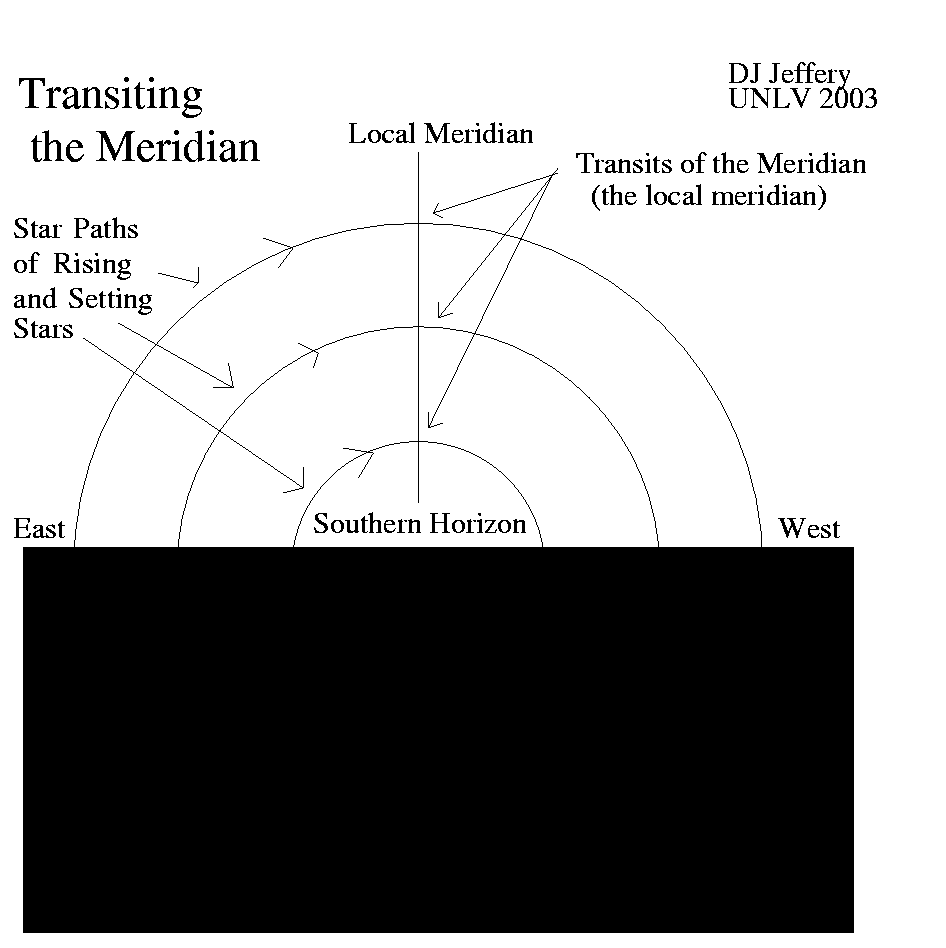
Caption: Astronomical objects transiting (i.e., crossing) the celestial meridian.
The south celestial pole (SCP) is just barely below the horizon which means the observer is just barely north of the equator.
Credit/Permission: © David Jeffery, 2003 / Own work. Image link: Itself.
The act of transiting meridian is called a transit.
The times of transits for astro-bodies are frequently tabulated or automatically calculated.
-
Question: What is the special name for when the
Sun transits
the meridian?
- Midnight.
- Fall.
- Noon.
Answer 1 and 3 are both right.Answer 3 is the Sun's upper meridan transit (upper culmination: highest altitude transit) which is usually what one means if one says meridian transit sans qualification.
Answer 1 is the Sun's lower meridian transit (lower culmination: lowest altitude transtit) which is often neglected since it usually occurs below the horizon.
Actually, both meridian transits will occur above/below the horizon for circumpolar objects which the Sun is if you are near enough to the Earth's poles.
Note, we are NOT referring to clock noon and clock midnight. We are referring to solar noon and solar midnight. In the old days, clocks were set by local solar time and that was good enough. But once railroads and railroad schedules came along, time had to be standardized for fairly large regions of the Earth, and so standard time was invented.
- The Equatorial Coordinate System:
The third way to locate astro-bodies is using equatorial coordinates. This way is much more precise than using constellations and is much more time-independent than using horizontal coordinates.
Equatorial coordinates are used for catalogs and permanent records.
The equatorial coordinates are explicated and illustrated in the three figures below (local link / general link: celestial_sphere_003_eqcoord.html; local link / general link: celestial_sphere_animation.html; local link / general link: sky_map_all_sky.html).
- The Equatorial Coordinate System in Moderate Detail (Reading Only):
Now we describe the equatorial coordinate system in moderate detail. In a classroom lecture, the discussion below is given with the figures above.
The viewing center of the equatorial coordinates is any place on Earth.
-
The Earth is sufficiently small
that corrections for the parallax due
to moving around on the Earth are usually
negligible.
Correctly are usually only needed for very close bodies like artificial satellites orbiting the Earth, the Moon, and asteroids and comets make close approaches to Earth.
Astro-bodies are located north or south of celestial equator along meridians by a "latitude" angle called declination (dec) which is measured using the units degree (1/360 of a circle), arcminute (1/60 of a degree and abbreviated by a ' symbol), and arcsecond (1/60 of an arcminute and abbreviated by a '' symbol).
Declination is positive to the north and negative to the south.
-
For example, the
NCP
is at 90° declination.
and the
SCP
is at -90° declination.
-
Using hours,
minutes, and seconds for angle measurement makes sense in the context of
right ascension
The celestial sphere rotates (from geocentric point of view) rotates westward 1 hour in 1 hour, 1 minute in 1 minute, and 1 second in 1 second.
But those time units are for sidereal time NOT ordinary time.
The sidereal day is the time for the Earth to rotate once relative to the fixed stars, NOT relative to the Sun.
The mean sidereal day is 0.99726958 standard solar days or 86164.1 s.
The other sidereal time units follow from the mean sidereal day by the conventional factors.
Usually, we won't bother to point out the difference between sidereal time and ordinary time measurement since it is qualitatively small.
We discuss the reason for sidereal time below in section The Sun on the Celestial Sphere.
Since right ascension is measured eastward on celestial sphere, the right ascension for any point on the sky fixed in horizontal coordinates increases with time.
For example, if at midnight 0 RA transits the meridian, at just a little less than 1 am (i.e., one sidereal hour later) 1 hour RA transits the meridian, and so on.
Since the celestial sphere rotates around the Earth every day, all RAs are visible above the horizon.
-
If you are NOT on the
equator, they are all present
somewhere on the sky above the
horizon all the time.
If you are EXACTLY on the equator in an ideal sense, then you can only see half of the RAs at any one time. But because celestial sphere rotates around the Earth once per day, you see all RAs in a day.
-
A little geometry
(which done in the figure at
local link: declination_altitude.html)
shows that
in Northern Hemisphere,
you cannot observe south of
declination
δ_S_circ = |L| - 90°
and in the Southern Hemisphere,
north of
declination
δ_N_circ = 90° - |L|.
Part of this change is due the physical motions of the Earth and the astro-bodies through space.
For astro-bodies in the Solar System, these changes are relatively fast, and so the equatorial coordinates of the astro-bodies must continually be recalculated. Fortunately, nowadays computers to this for us effortlessly. In the past, such calculations were often the main job of mathematical astronomers.
For extra-solar-system astro-bodies the changes are relatively slow, and so the equatorial coordinates of the astro-bodies do NOT need continually be recalculation.
But updates for the nearest extra-solar-system astro-bodies would have to made just for relatively physical motions.
However, the equatorial coordinates change intrinsically for another reason: the axial precession of the Earth's axis.
The equatorial coordinates are tied to the Earth's equator and the Earth's axis. The axial precession causes the orientation of the Earth's equator and the Earth's axis to vary slowly in time.
This motion causes slow continuous change of equatorial coordinates and catalogs have to be updated every 10 years or less to account for it.
You may ask why NOT have a coordinate system that does NOT have an intrinsic variation like equatorial coordinates.
There are such coordinate systems, but having a coordinate system tied to the Earth's equator and the Earth's axis is useful. It allows to us easily comprehend the motions of objects as the Earth rotates daily and to relate longitude and latitude to what can be seen in sky and when it can be seen.
So with we stick with equatorial coordinates for most ordinary astronomical work.
We describe axial precession below in section Axial Precession.
- Conversion Between Equatorial Coordinates and Horizontal Coordinates (Not Required for the RHST):
General conversion formulae require spherical trigonometry---which is hard.
If the azimuth is 0° or 180° (i.e., the astronomical object is transiting the celestial meridian), the conversion is easy if you know the right ascension (RA). You just have to relate declination (Dec,δ) and altitude from, respectively, NCP or SCP. The relationship formulae are given and derived in Celestial sphere file: celestial_sphere_005_circumpolar.html: Declination and Altitude.
- The Horizontal Coordinate System:
-
The field of astronomy
dealing with location is called astrometry---which
is a pretty descriptive name.
Here, we just discuss 3 main ways of locating astro-bodies on the celestial sphere and, briefly, the conversions between the second and third ways.
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 2 problems 16--21.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 2.
- The Sun on the Celestial Sphere
-
Now the extra-solar-system
astro-bodies
do slowly change relative positions on the
celestial sphere
(not just their
equatorial coordinates)
over time because of their own and the Sun's motion through space.
-
The Earth's Orbit and the Ecliptic Plane:
We usually say that the Earth physically orbits the Sun or it orbits the Sun relative to the fixed stars and these statements are correct. But recall the statements are shorthands. More exactly, the Earth orbits the Solar-System center of mass (which is nearly at the Sun) in center-of-mass (CM) inertial frame of the Solar System. Also recall all inertial frames do NOT rotate relative to the bulk mass-energy of the observable universe (except maybe near black holes???), and so there is an absolute rotation for the observable universe even though there is NO absolute space as theorized by Isaac Newton (1643--1727). And so the Earth orbits the Solar-System center of mass relative to the observable universe.
For an illustration of the Earth physically orbiting the Sun, see figure below (local link / general link: ecliptic_plane.html).
The plane of the Earth's orbit is called the ecliptic plane
The perpendicular to the ecliptic plane and the Earth's axis (and therefore the celestial axis) is tilted with respect to the ecliptic axis.
- The Ecliptic:
Because of the Earth's axial tilt, from the Earth's PERSPECTIVE, the ecliptic plane is also tilted by 23.4° from the Earth's equator and therefore by 23.4° from the celestial equator.
The ecliptic plane cuts the celestial sphere in a great circle which we call the ecliptic.
The ecliptic is the path of the Sun on the celestial sphere as it geometrically orbits Earth in a year---for which kind of year, see subsection Years: Solar, Sidereal, Common, Leap, Julian below.
-
As described above in subsection
The Earth's Orbit and the Ecliptic Plane,
the Earth physically
orbits the
Sun.
However, GEOMETRICALLY one describe either as orbiting the other.
Both perspectives are geometrically valid: which
one you use just depends on whether you take
Earth
or Sun as
your reference point.
For observational purposes, we often take the Earth as at rest and say the Sun oribts the Earth and moreover that the whole observable universe rotates once per day on the celestial axis.
The ecliptic plane is explicated in the figure below (local link / general link: season_001_ecliptic.html).
Also explicated are four special points on the ecliptic: two equinoxes and two solstices.
The TWO MOTIONS are added---but in a slightly complicated way since they are NOT along the same great circle---you need spherical trigonometry to do the "addition"---but let's NOT go there today.
The TWO MOTIONS do result in a difference between solar day and sidereal day which we explicate the subsection Solar Day and Sidereal Day below.
-
Note, there are 360° in a circle and about 365.25 days in
a year.
Thus the Sun moves about 1 degree per day relative to the fixed stars.
This is probably the main reasons why the ancient Babylonian astronomers Babylonians settled 360° in a circle. See babylonian_360_degrees.html for the whole story and more.
- Solar Day and Sidereal Day:
The fact of the TWO MOTIONS of the Sun on the celestial sphere (discussed in the subsection The Ecliptic above) is the cause of the distinction between solar day (solar noon to solar noon) and sidereal day (rotation period relative to the observable universe or to good approximation the fixed stars).
The distinction is explicated in the figure below (local link / general link: sidereal_solar_time.html) from the Earth orbiting the fixed Sun perspective.
- The Stars Rise Earlier Every Day:
The eastward motion of the Sun on the ecliptic also explains the solar time daily advance of the day sky and night sky, and of celestial phenomena like rising, setting, and transiting the meridian for objects that are moving relatively slowly on the celestial sphere compared to the Sun.
-
Yours truly mnemonicks this daily advance by the mnemonic:
The stars rise earlier every day.
Now the Sun continuously moves eastward relative to the relatively unmoving bodies.
But relative to the Sun, they are moving westward.
This means that every day the relatively unmoving objects will rise earlier, transit the meridian earlier, and set earlier than the day before according to solar time which is approximately standard time.
-
In fact, the stars
and astro-bodies
with very slow motions on the celestial sphere
(that are NOT
circumpolar objects)
rise earlier by the difference between the
mean solar day ≅ 86400.002 s (J2000)
(i.e., the mean time from
solar noon
to solar noon)
and the
mean sidereal day ≅ 86164.1 s.
Thus, earlier by 86400.002 s - 86164.1 s = 235.9 s = 3m:55.9s ≅ 4 minutes.
The figure below (local link / general link: zodiac_ecliptic.html). makes the solar time advance clear.
- Years: Solar, Sidereal, Common, Leap, Julian:
There are actually two kinds of astronomical year for the Earth to orbit Sun: the sidereal year = 365.256363004 days (J2000) and the solar year = 365.2421897 days (J2000) (AKA the tropical year) which differ in their decimal fractions:
- The physical year
(i.e., relative to the observable universe
or to good approximation the fixed stars)
is called the
sidereal year = 365.256363004 days (J2000).
Traditionally "sidereal" meant relative to the
fixed stars, but in modern times
it means relative to the
observable universe.
Note, J2000 means value as of the year 2000. Due to astronomical perturbations, all Solar System quantities vary slowly with time, and so values cited to a large number of significant figures are only exactly valid at one time. The year 2000 is the standard reference time for the 21st century.
To be a bit more precise J2000 means 2000 Jan01, noon Terrestrial Time (TT)). Terrestrial Time is pretty darn close to Coordinated Universal Time which is pretty nearly Greenwich Mean Time which is nearly solar time in Greenwich, England (which is near London).
For exact astronomy, one has to be exact about one's time system.
- The solar year = 365.2421897 days (J2000)
(AKA the tropical year).
This is the time
for the Sun to cross the
celestial equator twice:
once going north (called the vernal equinox (c.Mar21))
once going south (called the fall equinox (c.Sep21).
It usually defined as the time
vernal equinox to
vernal equinox.
We discuss the equinoxes in the
subsection The Ecliptic above
and the subsection Equinoxes and Solstices below.
The difference between the sidereal year and the solar year is due to the Earth's axial precession (AKA precession of the equinoxes) which we explicate below in section Axial Precession.
They have thought of using everything else. There are lots of other kinds of years, in fact. See, e.g., Wikipedia: Year: Astronomical years and Wikipedia: List of calendars.
The modern civil Gregorian calendar uses the common year = 365 days exactly and the leap year = 366 days exactly.
Another year is the Julian year = 365.25 days (exact by definition) which is the approximate time-weighted average year of the Gregorian calendar years and the exact time-weighted average year of the Julian Calendar.
For a discussion of the Julian Calendar and its correction the Gregorian calendar, see the explication in the figure below (local link / general link: julius_caesar_tusculum_like.html).
- The Ecliptic:
But those changes arn't easily noticed in a human lifetime.
What is obvious is that the Solar System bodies (i.e., Sun, Moon, planets, asteroids, comets, spacecraft, etc.) do change position on the celestial sphere relative to the fixed stars over a human lifetime and often much shorter time scales.
In this section, we consider the Sun's motion on the celestial sphere.
The motion other Solar System bodies, we consider in section The Moon, Planets, Asteroids, and Comets on the Celestial Sphere.
- The Seasons
-
To understand, Earth's
seasons,
we will largely use the Sun-centered perspective.
- The Main Idea Via an Animation:
Recall the Earth's axis maintains the nearly same direction relative to the observable universe over relatively short time periods like a year and a human lifetime.
This illustrated in the animation in the figure below (local link / general link: earth_seasons_animation.html).
- EOF
- Solar Intensity and the Solar Year Cycle:
Let's now expand the explanation of the seasons in tedious detail.
First, the solstice seasons as explicated in the figure below (local link / general link: season_solstices.html).
In this subsection to be brief, we will just say solar intensity to mean the intensity of solar light received by the ground.
-
There is a special term,
insolation,
for the amount of solar energy received per unit area in some specified time.
I find this term a bit klutzy since one has to add "per unit time" in order make it an intensity.
The orientation effect is illustrated in the figure below (local link / general link: power_flux_area.html).
This is illustrated in the figure below (local link / general link: season_003_summer.html).
This is illustrated in the figure below (local link / general link: season_004_winter.html).
For the Southern Hemisphere, one has the same case as for the Northern Hemisphere, mutatis mutandis.
The orientation effect on solar intensity is the main reason for the seasons.
- At the Equinoxes:
The figure below (local link / general link: season_equinox.html) illustrates the Earth's situation at an equinox.
- How Does the Sun Traverse the Sky as the Seasons Change?
For some mid northern latitude the two figures below show how: from the perspective of (1) the horizontal coordinates (local link / general link: sunpath_equinox.html) and (2) the equatorial coordinates (local link / general link: celestial_sphere_004_day.html).
- What About the Elliptical Orbit of the Earth?
Actually, the Earth's orbit is NOT exactly a circular orbit. It is an elliptical orbit with the Sun at one focus.
The eccentricity e = 0.0167 = 1.67 % which means that the Earth's distance from the Sun varies up and down from the mean orbital radius by 1.67 %.
The perihelion is actually in the first week of January (on about January 3) and the aphelion in the early July (on about July 4).
This distance variation has some modulating effect on the seasons, but the dominant cause of the seasons is overwhelmingly the Earth's axial tilt.
-
Question: If the eccentricity of the
Earth's orbit
were significantly larger than e = 0.0167, would the eccentricity
have a more significant effect on the Earth's climate?
- Yes
- No.
- Maybe.
Answer 1 is right.Unless you also invoked some wild compensating effect, I think answer 1 is the only valid answer.
- Terrestial Heat Energy and the Earth's Energy Budget:
- The Main Source:
The light energy from the Sun is the MAIN SOURCE OF TERRESTRIAL HEAT ENERGY at ground level as explicated in the figure below.

Caption: The heat sources at the Earth surface. The 700 W/m**2 should be 170 W/m**2.
About 170 W/m**2 on average---an average over the whole Earth surface including both day and night sides---comes from the Sun and only 8*10**(-2) W/m**2 from geothermal heat flux (CW-46).
The 170 W/m**2 on average is what solar power has to rely on.
There is lots of solar power since there is lots of land, but the energy density (energy per square meter) is low.
That low density is a problem for solar power.
Credit/Permission: © David Jeffery, 2003 / Own work. Image link: Itself.
- Why Don't We Fry?
Of course, there is no net build up of heat energy---if there were, we'd just get hotter and hotter until we fried.
The Earth's surface is approximately in a steady state---a time independent state---NOT counting little variations like weather, seasons, global warming, etc.
All the heat energy to the Earth's surface we get mostly in the form of visible light (high temperature light) gets re-radiated back to space eventually as infrared light (low temperature light).
The situation is analogous to a house heated by a furnace in winter.
The figure below (local link / general link: heat_flow.html) explicates the heated house case.
- The Greenhouse Effect in Brief:
In the case of the Earth, the Earth's atmosphere constitutes the Earth's thermal insulation. Without the atmosphere the Earth's temperature would be lower than it is.
So the greenhouse effect---which is the thermal insulation effect of the Earth's atmosphere---is good---but only in the right amount.
We will return to the greenhouse effect in IAL 11: The Earth.
However, as a preview, the Earth's energy budget is illustrated in the figure below (local link / general link: earth_energy_budget_2.html).
- Seasonal Lag:
The equinoxes and solstices mark the astronomical start dates for their respective seasons: spring, summer, fall, winter.
Now judging from the heating effect of the Sun, one would at first glance think that the astronomical start dates would be about the middle of the climatic seasons. However, seasonal lag (mainly due the time it takes large bodies of water to heat and cool is of order a month (Wikipedia: Seasonal lag: On Earth). This makes the astronomical start dates reasonablly appropriate for the start dates of the climatic seasons.
For example for the Northern Hemisphere, the hottest period (i.e., July) is typically about a month after the summer solstice and the coldest period (i.e., January) is typically about a month after the winter solstice.
- Why Don't We Fry?
- Solar Intensity and the Solar Year Cycle:
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 2 problems 22--28.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 2.
- Axial Precession
-
The Earth's axis
exhibits an
axial precession.
-
The Kinematics of the Earth's Axial Precession:
Kinematics is the description of motion WITHOUT reference to causes.
The kinematics of the Earth's axial precession is explicated by the figure below (local link / general link: axial_precession_animation.html).
- The Cause of the Axial Precession:
What is the cause of the axial precession?
An explication is given in the figure below (local link / general link: axial_precession_physics.html).
- The Axial Precession and the Equatorial Coordinates:
The axial precession is the main reason why the equatorial coordinates of extra-solar astro-bodies have to be updated continually for high accuracy/precision.
Equatorial coordinates are defined using the Earth's axis and the Earth's equator.
-
This is the good way to define the
equatorial coordinates.
The rotating Earth is our platform for observations.
Having coordinate system tied to that platform makes location and precise measurement of astronomical objects relatively straightforward.
The shift is small over a human lifetime, but precise astrometry requires updates at least every 10 years.
-
Nowadays, computers
give us continually updated
equatorial coordinates
if we want them.
- The Solar Year and the Sidereal Year:
The difference between the solar year and the sidereal year is due to the axial precession as explicated in the figure below (local link / general link: axial_precession_year.html).
- The Variation the Earth's Axial Tilt:
As well as the axial precession (which is a change direction without necessarily a change in Earth's axial tilt size), the Earth's axial tilt size does vary in time too as shown in the figure below (local link / general link: axial_tilt.html).
- The Cause of the Axial Precession:
A precession is the sweeping out of a cone or a double cone by a body's rotation axis. A double cone is illustrated in the figure below (local link / general link: double_cone.html).
- The Moon, Planets, Asteroids, and Comets on the Celestial Sphere
-
The Moon moves on
a great circle on the
celestial sphere
near the
ecliptic
and its direction is
EASTWARD relative to the
observable universe
like the Sun.
-
The Alignment of the Orbital Planes is Not Nearly Perfect:
The alignment of the orbital planes of the Solar System is NOT nearly perfect.
For example, the Moon's orbital plane is tilted by 5°, 9' from the ecliptic (Se-33). This tilt is illustrated in the figure below (local link / general link: earth_moon_system.html).
- EOF
- Planetary Configurations:
There is some recognized special arrangements of Earth, Sun, and planets.
These arrangements are called planetary configurations.
The figure below (local link / general link: planetary_configurations.html) illustrates the common planetary configurations.
For example, Moon and Venus are in near conjunction in the figure below.

Caption: "Three consecutive days of close conjunction between the Moon and Venus. Taken on 19, 20 and 21 of April 2007 in the evening."
The Moon moves east by about 12.2 degrees/day relative to the fixed stars and 13.2 degrees/day relative to the Sun.
In this image, we see the Moon move east of Venus and in image going to the left.
The motion of Venus on the celestial sphere is much slower for this epoch.
The closest point of near conjunction probably happened at some unobservable time when both bodies were below the horizon or lost in daylight.
A conjunction in which the Moon eclipses Venus is probably a bit rare since neither body orbits exactly in the ecliptic plane.
The Moon is a crescent at this phase because it is near the Sun, but that's NOT obvious in the image. If you click on the link to the image and then the image and magnify, then the crescentness of the Moon is seen.
Credit/Permission: © fdecomite, 2007 / Creative Commons CC BY-SA 2.0.
Image link: Wikipedia: File:Moon and Venus conjunctions.jpg.
- Apparent Retrograde Motion:
The planets as stated above, move EASTWARD MOST OF THE TIME on the celestial sphere, but they can move WESTWARD on it for relatively short times near opposition for superior planets or inferior conjunction for inferior planets.
This WESTWARD MOTION is called apparent retrograde motion---which is often abbreviated to "retrograde motion", especially when speaking historically of the Copernican Revolution (c.1543--c.1700) and earlier times when apparent retrograde motion was usually thought of as a motion in 3-dimensional outer space.
To explicate apparent retrograde motion, "apparent" as used in astro jargon, and retrograde motion in the modern sense, see the apparent retrograde motion on the celestial sphere of Mars in the figure below (local link / general link: apparent_retrograde_motion_mars.html).
To over-simplify for a moment, apparent retrograde motion is like observing a car move backward relative to the landscape when you are passing it.
When the car is far ahead or far behind it appears moving forward relative to the nearby landscape at least: i.e., curbs and shoulders and bushes by the roadside.
It is most easy to understand apparent retrograde motion from a top view of the Solar System (i.e., looking down from the NCP side of the ecliptic plane).
-
Note, the closer the planet
is to the Sun, the faster it moves
3-dimensional outer space
and also the less distance it has to travel since it is on a smaller orbit:
both things make its
angular velocity higher the
closser it is to the Sun.
The planet speed is a consequence of
Newtonian physics and
gravity.
The Apparent retrograde motion videos below further illustrate apparent retrograde motion.
-
Apparent retrograde motion videos
(i.e., Apparent retrograde motion
videos):
- Mars Retrograde Orbit Simulation | 0:23: What it looks like on the sky---except the lines joining the constellations are phoney. That thing whizzing by periodically is the Moon (see Richard Pogge, 2011: Mars Retrograde Motion during 1994/95) Short enough for the classroom.
- Retrograde Motion | 0:19: Not great, but it shows apparent retrograde motion from the two points of view in two panels at the same time. Short enough for the classroom.
-
We'll look at these geocentric models
in IAL 4: The History of Astronomy to Newton.
The historical issues are discussed IAL 4: The History of Astronomy to Newton: Nicolaus Copernicus (1473--1543) and Heliocentrism.
-
Question:Why do the Sun and
Moon NEVER have
apparent retrograde motion?
- Because they BOTH orbit the Earth relative to the observable universe in the center-of-mass (CM) inertial frame defined by the Earth's center of mass.
- Because they BOTH geometrically orbit the Earth in nearly circular orbits.
- Because they are BOTH round.
Answer 2 is rightYes, it is because Sun and Moon both geometrically orbit the Earth in nearly circular orbits. Thus, the situation for retrograde motion never arises.
Answer 1 is wrong. The Sun does NOT orbit the Earth in said center-of-mass (CM) inertial frame.
Note, the planets do NOT geometrically orbit the Earth in nearly circular orbits: they sort of geometrically orbit it in two compounded geometrical circular orbits. The compounded geometrical circular orbits leads to their apparent retrograde motion.
- Asteroids:
The asteroids mostly behave like small planets as objects on the sky: but they are unresolvable in ordinary observations and look star-like: hence the name asteroid which means star-like.
They mostly have orbits near the ecliptic plane and move counterclockwise as seen from above and have apparent retrograde motion when in opposition or inferior conjunction.
There are a few oddballs among the asteroids---a few with true retrograde motion (i.e., they orbit clockwise when viewed from the NCP (see Wikipedia: Retrograde motion: Asteroids, comets, and Kuiper belt objects) and probably a few with very high tilts to their orbital planes relative to the ecliptic plane.
We will discuss asteroids later in IAL 16: Minor Planets, Asteroids, Icy Bodies, Meteoroids, and Target Earth.
Besides asteroids, there are icy-rocky bodies in various resevoirs of the outer Solar System most famously trans-Neptunian objects that dwell beyond about the orbit of Neptune.
Our remarks about asteroids apply generally to these outer-solar-system bodies too, but they are a more diverse population in orbital behavior.
For images and videos on asteroids, see the figure below (local link / general link: asteroid_collage.html).
- Comets:
What of comets?
First, see the great comet film in the figure below (local link / general link: coronal_mass_ejection_comet.html).
Well, comets have rather different orbits from the astro-bodies we've discussed above.
Comets have highly elliptical orbits with huge eccentricities. They come in two broad classes: short-period comets and long-period comets (Se-569).
The short-period comets have orbital periods less than about 200 YEARS, have orbital inclinations that are usually less than 30°, and mostly orbit counterclockwise about the Sun (looking down from the north ecliptic axis direction).
Long-period comets can have orbital periods from 200 years to millions and sometimes to infinity (i.e., they escape the Solar System). Their orbits have random orientations and can be clockwise or counterclockwise for any pole direction you choose.
The figure below (local link / general link: comet_orbits.html) shows a cartoon of the orbits of comets including long-period comets.
Maybe one day a bad comet will thwack us.
The long-haired stars have always been considered portentous, ominous. See Halley's comet figure below (local link / general link: bayeux_tapestry.html).
More about comets is given in IAL 10: Solar System Formation and IAL 17: Pluto, Icy Bodies, Kuiper Belt, Oort Cloud, and Comets.
- See Comet Videos:
See Comet videos below (local link / general link: videos_comets.html).
- Planetary Configurations:
The planets and asteroids move on great circles on the celestial sphere near the ecliptic and their direction is EASTWARD MOST OF THE TIME relative to the observable universe like the Sun.
-
Of course, we are NOT counting the daily
westward motion of the
celestial sphere
about celestial axis.
The celestial sphere
carries the
Sun,
Moon,
planets,
fixed stars, etc.
with it in its westward motion.
The near alignment of planet and Moon orbits is due to the formation history of the Solar System which is discussed in IAL 10: Solar System Formation.
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 2 problems 25--36 on the seasons and the motions of the Solar System astro-bodies on the celestial sphere.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 2.
- Constellations: Reading Only
-
Here, we only give a brief discussion of
constellations which
complements the discussion given above in
subsection Constellations as Skymarks.
- Naked-Eye Astronomy:
But to discuss constellations, we need to discuss what class of stars they are made of---that class is the set of stars that are those visible to the naked eye: see the figure below.
The number of stars that one can see with the naked eye under ordinary good observing conditions is estimated to be only about 5600 (Wikipedia: Naked eye astronomy)---they are NOT infinite---but maybe uncountable. Under exceptional conditions many more could be seen. Under Las Vegas maybe 10 at a first glance.
Of course, everyone's scotopic vision is a bit different, and so some people can see more than others. Also extraordinary good observing conditions allow you to see more stars.
-
Naked eye astronomy is frequently
considered erotic by search engines.
See the naked human eye
in the figure below.

Credit/Permission: © Petr Novak, Wikipedia (AKA User:Che), 2005 / Creative Commons CC BY-SA 2.5.
Image link: Wikipedia: File:Eye iris.jpg.
-
Question: Can the naked-eye stars
be seen all at once?
- Yes.
- No. Sky conditions can hide stars: daylight, clouds, etc.
- No. Half the
celestial sphere is
occulted (i.e., hidden) by the Earth.
Answers 2 and 3 are right.Just as a guess maybe you can see of order 1000 on a clear night.
Of course, when you use telescope or binoculars, you see vastly more stars.
-
For comparison, the diameter of the disk of the
Milky Way is
about 30 kpc as it is usually defined
(CK-379).
- Grouping Stars:
On the size scale of our local region in the Milky Way, stars are rather RANDOMLY located in 3-dimensional space.
Thus, these local stars are rather RANDOMLY located on the 2-dimensional celestial sphere when they are projected onto that remote imaginary sphere from the center of the Earth.
-
Only rather RANDOMLY because
the local stars
have some overall ordering because of the local structure of
the spiral arms
of the Milky Way.
-
They are NOT really fixed since they and the
Sun are orbiting the
Galactic center
with periods of order 200 Myr: the
Sun's
period is 220 Myr
(FK-565).
The orbits, by the way, are NOT fixed either. The stars are subject to constant small gravitational perturbations, and so their motions are a bit randomized.
Because the fixed stars are relatively fixed and relatively RANDOMLY located on the sky, they can be grouped into relatively fixed, relatively arbitrary groupings.
-
At least mostly ARBITRARY groupings.
The fixed stars in such groupings
usually have no strong gravitational interaction with each other and are often far apart
in 3-dimensional space.
They may be just close in angular position on the
celestial sphere.
Of course, some actual physical groupings do occur: i.e., groups of gravitationally bound stars which are called star clusters if there are many stars or multiple star systems if there are few stars (i.e., 2 or 3 or a few).
- Finding Six Constellations:
Consider the winter sky map in the figure below (local link / general link: sky_map_winter.html) with constellations labeled on.
The sky map is about what one would see in winter from a mid-northern latitude.
We will learn how to find 6 constellations using the sky map.
- Ursa Major with recognizable asterism the Big Dipper.
- Ursa Minor with identifiable star Polaris easily found using the POINTER STARS of the Big Dipper.
- Cassiopeia which has a very recognizable W SHAPE.
These circumpolar constellations can be seen at any time of the year from mid-northern latitude. They are always above the horizon---you just can't see them in the daylight. They, of course, circle the celestial axis that runs nearly through Polaris every day. Where they are relative to the ground on their circular paths at night depends on the time of the year.
-
Remember the solar time
advance of daily celestial phenomena of relatively unmoving bodies
that was discussed in
section The Sun on the Celestial Sphere---mnemonicked
by the phrase "the stars rise earlier every day".
This effects the motions of circumpolar stars too, of course.
For example, their two daily transits of the meridian (one at maximum altitude and one at minimum altitude) will occur earlier as days advance.

Caption: Old Man Orion---lord of the winter sky---he's always looming over you when your out freezing in the night.
The constellation Orion with labeled bright stars: Betelgeuse, Rigel, etc.
The constellation is named for the mythical Orion, the hunter.
Credit/Permission: © Anirban Nandi (AKA User:Anirban13), 2013 / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia: File:Orion constellation with star labels.jpg.
Orion is NOT circumpolar since it is too near celestial equator---actually Orion straddles the celestial equator.
So Orion is above the horizon for only about half the day---nearly exactly half a day on the equator.
In summer (in the Northern Hemisphere), the day side of Earth faces Orion and it's NOT seen.
In winter (in the Northern Hemisphere), the night side of Earth faces Orion and Orion lords it over the winter night.
To the lower left of Orion is Canis Major (the greater dog) which is traditionally one of Orion's hunting dogs.
As a constellation, Canis Major is NOT very obvious, but its brightest star Sirius (the Dog Star) is the brightest star in the sky and on average the brightest object in the sky after the Sun, the Moon, Venus, and Jupiter.
-
Mars and
Mercury are brighter than
Sirius at some times.
Sirius can even been seen in daytime if the sky is very clear, Sirius high in the sky, and the Sun low.
To the northwest of Aldebaran and above the ecliptic is a tight little group of stars called the Pleiades---just a small grouping on the sky map.
The Pleiades are shown in the figure below (local link / general link: pleiades.html).
Only 6 Pleiades are visible to the naked eye under moderate conditions, but up to 14 have been claimed for great conditions by what were probably very sharp-eyed observers (see SEDS: Pleiades (AKA Messier 45)).
The Pleiades are actually a gravitationally bound open star cluster of which most members are NOT visible to the naked eye. The total number of stars is more than 1000 NOT counting unresolved binaries (see Wikipedia: Pleiades: Composition).
But you can see all the constellation on the all-sky sky map in the figure below (local link / general link: sky_map_all_sky.html). These, of course, are the modern IAU-defined 88 constellations (which we discuss below in section The Modern Astronomical Constellations) and only their abbreviated names are shown: see Wikipedia: 88 modern constellations: Modern constellations for the names and abbreviations.
- When Can You See Specific Constellations?
rises at sunrise, it will set at sunset and you will never see it---except possibly just at sunrise and sunset if you can make it out.Well, the circumpolar constellations above your local horizon you can always see on clear nights: e.g., at mid-northern latitudes Cassiopeia, Ursa Major, and Ursa Minor.
The circumpolar constellations below your local horizon you can never see. For mid-northern latitudes, those are all the far south constellations.
The other constellations are above the local horizon for part of the day, but if that part of the day is daylight, then you don't see them.
If a star or constellations star
But the non-circumpolar fixed stars rise earlier every day due to the Earth's motion around the Sun as we discussed in section The Sun on the Celestial Sphere.
So every non-circumpolar star and constellation cycles through all rising times in the course of a year.
The figure below (local link / general link: zodiac_ecliptic.html) illustrates this for the zodiac constellations.
- Heliacal Rising: Reading Only:
In olden days when people used pay more attention to the sky, the rising of particular stars with sunrise---the heliacal rising---was sometimes taken as marking particular times of the year.
-
Before its heliacal rising,
a star rises in the daytime and can't
be seen usually.
But as it keeps rising earlier, eventually it rises with the Sun or a bit earlier and can be seen---this is its heliacal rising.
- Why Do We Have the Constellations We Do:
We CANNOT know for sure how ANCIENT CONSTELLATIONS were settled on or why. But for some of the folklore, see the Stars And Constellations | 3:11 and Carl Sagan's Cosmos - Constellations | 3:57 videos in Constellation videos (see below (local link / general link: constellation_videos.html).
The Big Dipper was certainly so called because it looks like a set of dots outlining a dipper (a cup with a long handle)---but certainly it was NOT so identified by all cultures: e.g., in the Hiberno-British Isles, it is sometimes called THE PLOUGH or THE WAIN (the Wagon) or variations thereof (see Wikipedia: Big Dipper: Europe).
Without connecting lines---except for the Big Dipper and the Little Dipper---the shapes of constellations have no/almost no relation to the names assigned to them.
The names of constellations names were no doubt often assigned to honor a god or a myth.
For example, Taurus (the Bull) goes back at least to the Babylonian astronomers of the 7th century BCE and, perhaps, much earlier (Wikipedia: Taurus history) and may honor a bull god or a sacred bull. The ancient Greeks associated Taurus with Zeus in his bull disguise---you recall Europa and all that sorry history.
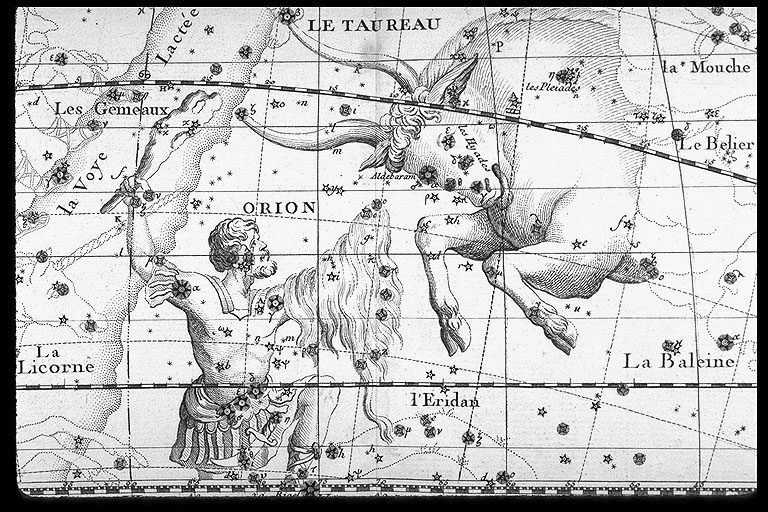
Credit/Permission: John Flamstead (1646--1719) (Atlas celeste, Paris, 1776, Ed. J. Fortin) / Public domain.
Image link: Itself.
Download site: Linda Hall Library, 30 Flamsteed, John. Atlas celeste. Ed. J. Fortin. Paris, 1776. (dead link).
Then there is Orion again: see the figure below (local link / general link: betelgeuse.html).
And also individual astronomers making sky maps often made up new constellations to please themselves.
The upshot is that before circa 1900, sky maps often contained a mixture of traditional constellations and ones made up by the astronomer making the sky map.
The following sky map from Chinese astronomy probably exhibits both kinds of constellations.
Greek astronomer Ptolemy (c.100--c.170 CE) in his star catalogue groups 1022 fixed stars in 48 constellations many (most???) following Babylonian constellations (No-113).
Ptolemy's constellations are the basic set of classical constellations from which modern constellations of the Northern Hemisphere sky are derived.
- The Zodiac Constellations:
These classical constellations include the zodiac constellations.
-
Question: What is special about the
zodiac constellations?
Answers 1 and 2 are right.Actually, answer 1 is only sort of right:
One would think---if one knew better---that the zodiac is the set of zodiac constellations which is the set of 12 constellations that straddle the ecliptic and through which the Sun passes in the course of a year.
But in astrology, the zodiac is the set of zodiac signs, and NOT the zodiac constellations.
The zodiac signs are just twelve 30-degree segments on ecliptic measured from the vernal equinox (i.e., where the Sun crosses the ecliptic on about Mar21 each year).
The zodiac signs are named for the zodiac constellations that used to be in the zodiac signs about 2500 years ago (see Wikipedia: Zodiac: Early history).
The vernal equinox has shifted due to the axial precession since astrology was set up over 2500 years ago, and so the zodiac signs NO longer contain the zodiac constellations---but the astrologers have never worried about this.
In astrology, your sign is the zodiac sign the Sun is when you were born. For example, The Sun is in the sign of Aries in the time period about Mar21--Apr20. For the sign of Aries illustrated, see the figure below (local link / general link: tres_riche_heures_03_march.html).
Answer 3 is wrong, NOT all the zodiac constellations are all animals: there are Gemini (the Twins) and Libra (the Weighing Scales) for examples.
But the word zodiac is from the Greek and means circle of animals.
- Southern Constellations:
When Europeans first visited the Southern Hemisphere 15th century, they saw stars they'd never seen before and they eventually started inventing new constellations---the idea of asking the native southern hemispherians for what constellations were already there probably never occurred to the Europeans.
Who sanctioned the inventions?
The authors themselves essentially. If you make a book of sky maps, you could choose your own constellations. A book of sky maps was a major production and authors were authoritative. The authors mostly used traditional constellations, but felt free to invent new ones, particularly for the Southern Hemisphere.
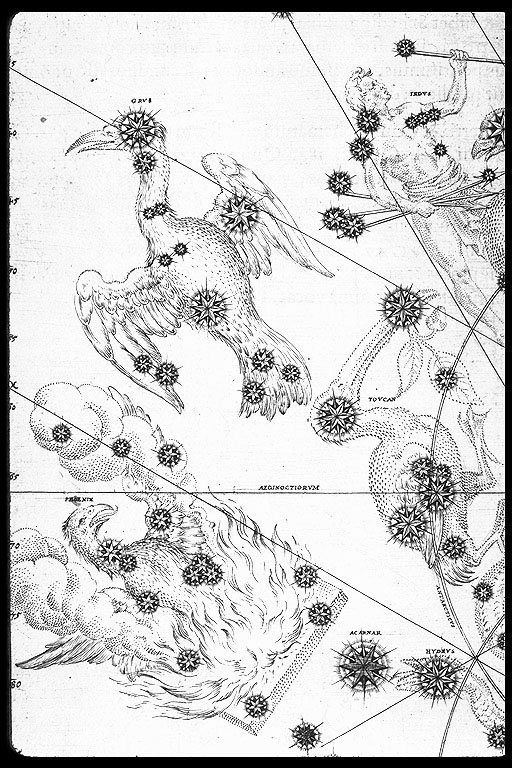
Caption: Tucana (Toucan), Grus (the Crane), and Phoenix.
Credit/Permission: Johann Bayer (1572--1625), Uranometria (Augsburg 1603) / Public domain.
Download site: Linda Hall Library, 9a. Continuation of Johann Bayer, Uranometria, 1603, alas a dead link.
Image link: Itself.
The first European southern constellations seem to have been introduced by Johann Bayer (1572--1625) in his Uranometria (Augsburg 1603).
He made up 12 new southern constellations including Tucana (Toucan), Grus (the Crane), and Phoenix (see the adjacent figure).
In the 17th and 18th centuries, there was a lot of making up of new constellations to fill in gaps between the ancient ones. Many of these didn't survive at all.
For examples of 16th century--18th century images of constellations see Constellations from the Great Celestial Atlases downloaded from the Linda Hall Library exhibit Out of This World: The Golden Age of the Celestial Atlas.
For more on constellations, see Constellation videos below (local link / general link: constellation_videos.html).
- The Modern Astronomical Constellations: Reading Only
-
In 1922, the
International Astronomical Union (IAU)
at its first meeting decided---perhaps arrogating to itself
the right to decide---on a fixed
set of IAU-defined 88 constellations
(see the figure below:
local link /
general link: iau_88_constellations.html).
So every equatorial coordinate location is in some constellation and only in that constellation.
Modern constellations are illustrated in the figure below (local link / general link: iau_pisces.html).
There are many listings of IAU-defined 88 constellations: e.g., Wikipedia. 88 modern constellations: Modern constellations.
-
The IAU-defined 88 constellations
include 14
humans/gods,
19 land animals,
10 water creatures,
9 birds,
2 insect ,
2 centaurs,
a head of hair
(Coma Berenices [Berenice's Hair]),
a serpent,
a dragon,
a flying horse
(Pegasus),
a river, and 29 inanimate objects
including a telescope and a
ship's sail.
There are more than 88 objects in the above list because some of the IAU-defined 88 constellations include multiple objects.
Note, Coma Berenices (Berenice's Hair) is the only IAU designated constellation named for an actual historical person or at least their hair: Queen Berenice II of Egypt (267/266--221 BCE), an ancestress of Cleopatra (69--30 BCE).
As noted above, any of these unofficial groupings, is an asterism.
In modern usage, the term asterism is NOT used for IAU-defined 88 constellations. But in older usage an asterism could be a synonym for constellation. In IAL, I will use asterism only in the modern sense.The most famous asterism is the Big Dipper which is still often called a constellation in its own right, but it is NOT in the IAU-defined 88 constellations: it is just part of Ursa Major (the Great Bear).
The Big Dipper and Ursa Major are show in the two figures below. (local link / general link: jeffery_big_dipper.html; local link / general link: polaris_ursa_minor_major.html).
Other well known asterisms are presented by Wikipedia: Asterism: Large or bright asterisms and Wikipedia: Former Constellation: List of former constellations.
- Why does Astronomy Still Bother with Constellations? Reading Only
-
Why does astronomy
still bother with
constellations?
As we argued above, we now understand that for the most part
they have no real physical significance---just arbitrary groupings of stars
rather randomly distributed on the
celestial sphere.
Partially, it is just that astronomers and folks in general are FOND of their constellations---they're traditional and part of the romance of astronomy---so we should keep them in an orderly fashion---for example, the Alien (see the figure below (local link / general link: alien_constellation_2.html).
The modern astronomical constellations (the regions on the sky) provide a useful rough and easily memorized location system---the constellations (the actual stars) act as SKYMARKS for the constellations (the regions on the sky). This was discussed above in subsection Constellations as Skymarks.
One can always locate an astronomical object precisely using equatorial coordinates, but just for a rough position one can say the object is in such or such a constellation: i.e., in that region on the sky that is labeled by that constellation.
For example, Aldebaran is in Taurus---as indeed it always is.
For another example, one can say there is a bright supernova in Virgo. This is a relatively frequent occurrence since there is a large nearby galaxy cluster in Virgo called the Virgo cluster. Supernovae occur in galaxies, and so are relatively frequently found in the Virgo cluster, and hence in Virgo.
-
Supernovae
occur only a few times per century in large galaxies,
but if you are looking at many galaxies in a
galaxy cluster, you'll see them
much more often.
The locution object x is in constellation y, although perfectly natural given the modern definition of constellation, does have astrological suggestiveness as if there was a magic sympathy between object and constellation---Venus is Virgo or Venus is in Taurus---but this is just a vestige of where we've come from.
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 2 problems 38--47 on constellations.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 2.
- Parallax
