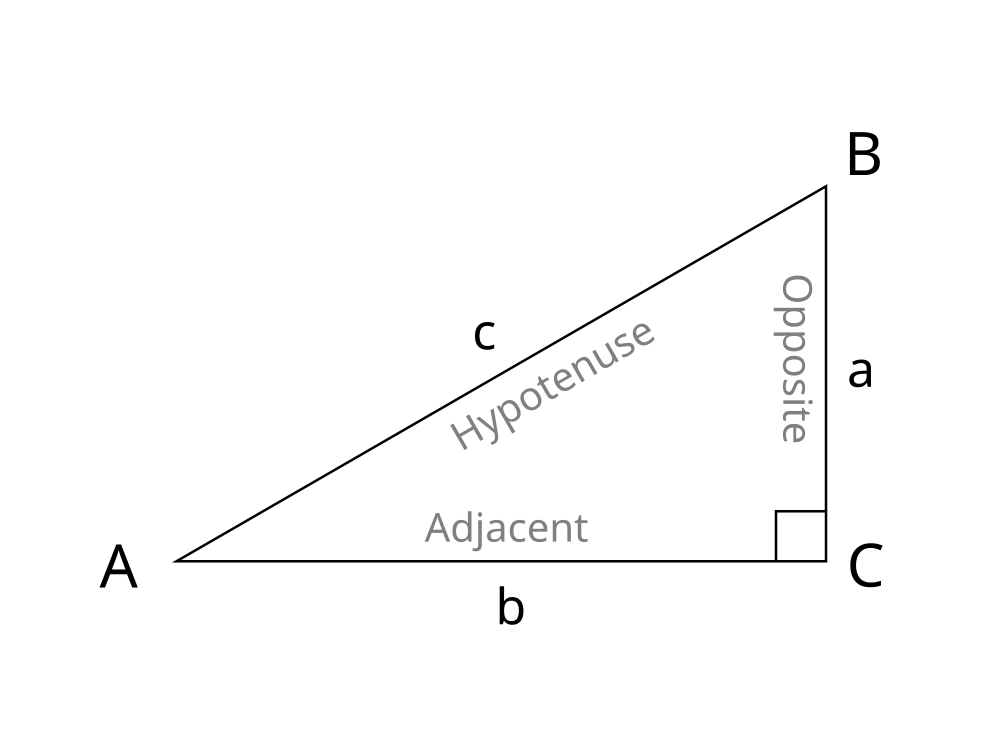
Right triangle and trigonometry

    Caption: A right triangle illustrating the meaning of some common terms of trigonometry: adjacent, opposite, hypotenuse. The angles of the right triangle are A = 30°, B = 60°, and C = 90°.

    Angle A is a parallax if it were measured by moving along the opposite (which is the baseline for the parallax) and measuring the shift in angular position of vertex A (which is just angle A itself) against the background of remote reference points.

    We can calculate distance b using angle A and baseline distance "a" using trigonometry: 

      tan(A)=a/b , therefore  b=a/tan(A)  .
    If angle A is very small, we can make the small-angle approximation tan(A)≅A and obtain to 1st-order in small A 
      b=a/A  ,
    where angle A is measured in radians.

    Radians are the natural units for measuring angles---but they are NOT always convenient units since there are an irrational number of them in a circle: i.e., 2π = 6.283185307179586 .... The conversion formula from degrees to radians is 

      θ(radians) = θ(°)*(2π radians/360°).
    Astro-bodies are usually so remote that their parallaxes are tiny for any baseline that we can use. Thus, the small-angle approximation virtually always gives negligible error.

    Credit/Permission: User:TheOtherJesse, 2007 / Public domain.
    Image link: Wikipedia: File:TrigonometryTriangle.svg.
    Local file: local link: right_triangle.html.
    File: Trigonometry file: right_triangle.html.