-
Observationally, being on the
main sequence
means that a star is located on that band on the
HR diagram
that has been called the main sequence.
See the figure below
(local link /
general link: star_hr_named_stars.html).
- is used up relatively slowly.
- is never used up at all.
- is used up relatively rapidly.
From a combination of observation and modeling, we now know a lot
about
main sequence stars
which are, in fact, the relatively easy stars to understand.
Physically, being on the main sequence means that a star is stably doing hydrogen burning (i.e., fusing hydrogen nuclei to helium nuclei) in its core and that its structure is very nearly in hydrostatic equilibrium (i.e., it is very nearly a fluid at rest).
The heat energy released by the nuclear fusion compensates for the energy the star loses by radiating electromagnetic radiation (EMR) continuously into space.
Main sequence stars are very nearly in STEADY STATE (i.e., an unchanging state) for long periods of time.
-
Question: The near STEADY-STATE condition is possible
because the hydrogen fuel:
Answer 1 is right.
The hydrogen fuel is used up as the hydrogen is converted to helium.
-
This section is largely a recapitulation of
IAL 8:
The Sun: 5. Nuclear Fusion in the Sun, but some new aspects are presented.
- Nuclear Physics:
Atoms consist of negatively charged electrons in a swarm about a nucleus made of positively charged protons and neutral neutrons.
See the figure below (local link / general link: atom_nucleus_symbol.html).
But we can say nuclei are held together against the electrostatic repulsion of the protons by the strong nuclear force.
The strong nuclear force is a very strong force, but it is very short range. It acts only over a distance of 10**(-15) meters or less. This distance of 10**(-15) meters is 10**5 times smaller than an atom's size.
Thus, the protons and neutrons in a nucleus are compacted close together within about 10**(-15) meters of their nearest neighbors and nuclei have a size scale of order 10**(-15) to 10**(-14) meters depending on the number of protons and neutrons.
- Explication of Isotopes:
Some explication of isotopes is needed for our understanding nuclear physics. This explication is given in the figure below (local link / general link: isotopes.html).
- Hydrogen Burning in Main-Sequence Stars:
Now H nuclei strongly repel by the electrostatic force because they are like-charged particles.
In main-sequence stars, only in the cores is it ordinarily sufficiently hot and dense that the electrostatic repulsion can be overcome and the H nuclei can collide closely enough that the strong nuclear force can bind them (i.e., fuse them).
Note, astrophysicists, usually call fusion, nuclear burning because the fusion process is the nuclear analogue of chemical burning.
In main-sequence stars, overall process of fusing of H nuclei is a nuclear burning of hydrogen (H, Z=1) to helium (He, Z=2) which is usually just called hydrogen burning.
The first step in hydrogen burning (i.e., H-to-He-4 burning) in main-sequence stars is illustrated in the figure below (local link / general link: nuclear_burning_pp.html).
But the final product in stellar hydrogen burning is the very stable He-4 nucleus.
There are several H-to-He-4 burning processes in stars. The figure below (local link / general link: nuclear_burning_processes.html) illustrates the two dominant ones: the proton-proton (PP) chain reaction and the CNO cycle.
We will just look at the PPI chain in detail to illustrate a nuclear burning chain. See the figure below (local link / general link: nuclear_burning_ppi_chain.html).
In the carbon cycle, the carbon nucleus acts as a catalyst: i.e., a reactant that facilitates the process without being destroyed in a net sense in the process. We will NOT go into details though.
-
Hans Behte (1906--2005)
discovered the carbon cycle in 1938. In the early 1930s, he left Germany because of
the Nazis and in WWII he was the leader of the theory group
at Los Alamos in the Manhatten Project.
He was almost certainly the last of the great pre-war generation physicists.
4H + 2 electrons to He-4 + 2 neutrinos + heat energy (HRW-1107; Cl-390). The heat energy is in the form of kinetic energy of the particles and photons. The neutrinos mostly just freely escape the Sun, fly off into space, and have very little effect on the universe it seems.- Stellar Lifetime and the Sun's Lifetime:
Stellar lifetimes and main-sequence lifetime can be calculated. We consider these in general below in subsection Main-Sequence Lifetimes.
Here let's just ask how long is the Sun's main sequence lifetime? For the answer, see the figure below (local link / general link: sun_lifetime_estimate.html).
-
Question: How long is the Sun's
main sequence lifetime?
- About 10 Gyr.
- About 20 Gyr.
- There is NOT enough information to say.
Answer 1 is right.The Sun's age ≅ 4.6 Gyr , and so it is about half done with its main sequence lifetime.
The main sequence lifetime of a star is about 90 % of its total life as a nuclear-burning star???? (HI-330), and so to 1st order the main sequence lifetime is the total nuclear-burning lifetime.
Thus, the Sun is about half through its life.
- Explication of Isotopes:
-
Nuclear burning
is stable on the
main sequence.
By STABLE we mean the nuclear burning neither just turns off suddenly nor goes into a thermonuclear runaway and blows up the star.
The cartoon in the figure below (local link / general link: stability_mechanical.html) illustrates the STABILITY in general via a mechanics analogue.
A RULER balanced on a finger is an example of an unstable system.
Balance scales take advantage of
instability: their instability allows a fine determination of mass.
Hydrogen burning
in the Sun and all
main sequence stars
is STABLE due to the process
discussed in the figure below
(local link /
general link: sun_hydrogen_burning_stability.html).
Controlled fusion
and fusion power are explicated in
the figure below
(local link /
general link: nuclear_fusion_deuteron_triton.html).
A practical example of stability is all buildings. When kicked
they don't fall down---one hopes NOT even when they are kicked
really hard.
To recapitulate from
IAL 8: The Sun:
Controlled Fusion and Fusion Power,
down here on Earth we would like to have
STABLE hydrogen burning
or, as it is called,
controlled fusion
for fusion power.
-
As noted in
IAL 20: Stars Basics II:
Modeling Stars,
a full general discussion of star
modeling is beyond the scope of
Introductory Astronomy Lectures (IAL).
However, we do touch on aspects of
the star
modeling.
- The modeling of the interior of the star below the photosphere which is modeling stellar structure. In this section, we will expand on some aspects of modeling stellar structure
- The modeling of the stellar atmosphere which is from the photosphere outward. We touched on this in IAL 8: The Sun: The Photosphere. We will do NO more on this modeling.
- The BASIC CONTROLLING STELLAR PARAMETERS:
stellar mass
and composition.
Usually, somewhat less important controlling paramters are rotation and having a close binary companion.
- Known physics:
convection,
thermodynamics,
hydrodynamics,
hydrostatics,
Newtonian physics,
nuclear physics
(especially
nuclear burning rates
which are functions of temperature, density, and composition),
quantum mechanics,
radiative transfer,
statistical mechanics,
thermodynamics,
and whatever other physics theory
is needed.
- The 4 equations
of stellar structure which we explicate below in subsection
The 4 Equations of Stellar Structure.
Note, the
4 equations
of stellar structure are simplified in that they do NOT include the
effects of stellar rotation
and having a
close binary companion.
Also, convection is treated in a simplified
approximate 1-dimensional treatment.
The simplifications can be eliminated in more advanced
star
modeling, but discussion of
that is well beyond the scope of
Introductory Astronomy Lectures (IAL).
- Using numerical methods
on the computer to solve
simultaneously the
4 equations
of stellar structure.
Analytic solutions
are NOT possible.
- The 4 Equations of Stellar Structure:
The 4 equations of stellar structure are explicated in the figure below (local link / general link: stellar_structure_4_equations.html).
We derive and discuss the stellar hydrostatic equilibrium equation in the figure below (local link / general link: hydrostatic_equilibrium.html).
-
Question: The requirement of
hydrostatic equilibrium
means that pressure:
- increases with depth.
- stays constant with depth.
- decreases with depth.
Answer 1 is right.This is true in stars, in the Earth's atmosphere, in the oceans, and in a bottle of water sitting at rest on table.
The pressure must increase with depth to sustain the greater overlying mass with depth.
- The Kind of Pressure in Ordinary Stars:
The pressure in ordinary stars (i.e., NOT white dwarfs, NOT neutron stars) is a combination of ordinary ideal gas pressure (provided by ions and electrons) and radiation pressure.
The radiation pressure component increases with importance with stellar mass: for a star of 1 M_☉, it is almost negligible; for a star of 8 M_☉, it is about 10 % of the central pressure and a smaller fraction as one moves away from the center (Cl-162--164).
The compact objects white dwarfs and neutron stars are held up by, respectively, degenerate electron gas pressure and degenerate neutron gas pressure. We discuss degeneracy pressure briefly in the figure below (local link / general link: gas_classical_quantum.html).
- An Example of a Stellar Structure Model:
As mentioned above, the equations of stellar structure can ONLY be solved on a computer to determine star models.
People have been doing so since the 1950s and nowadays the models can be quite sophisticated and accurate.
Stellar structure models of main sequence stars are particularly easy to model since they are time-independent or STEADY STATE to good approximation. Good stellar structure models for all spectral types are available. As aforesaid, stellar structure models allow us to know many things we CANNOT know by direct or indirect observations.
Pre- and post-main-sequence modeling is a lot tougher because the stars are evolving more rapidly and hydrostatic equilibrium is NOT always a good approximation.
As an example, we present a cartoon of a stellar structure model of the Sun in the figure below (local link / general link: sun_model_interior.html).
-
Note, the
star
modeling is divided into two realms
in practice:
-
i.e.,
as a function of radius coordinate from center to surface, giving
the star's
the density, pressure, temperature, interior luminosity (i.e., luminosity
from within a given radius), interior mass (i.e., mass within a given radius), etc.
They follow from stellar structure modeling using:
Here we will focus a bit on stellar structure modeling and in particular on the 4 equations of stellar structure and recapitulate a bit.
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 22 problems 16--21 on main sequence stars and stellar structure.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 22.
-
Well, we know heat energy is created in stars by
nuclear burning
in their cores and we know that it is radiated away. But how does
the heat energy get out? The "how" is, of course, part of the modeling
process discussed above: here we just go into qualitatively how the
energy is transported.
- Energy Transfer in Space and in Stars:
In space, the spreading out energy is mainly transported by free-streaming radiative transfer of EMR.
But how is it transported in stars. The heat energy transport in stars is mainly by two mechanisms: radiative transfer (but NOT free-streaming) and convection.
In the interior of a star, radiative transfer is always occurring and the process is essentially a photon random walk process that we discussed in IAL 6: Light and Electromagnetic Radiation (EMR): Photon Propagation.
- Convection Redux:
Convection is a universally important, macroscopic heat transfer process. It occurs in:
- almost stars including the Sun.
- the interior of the Earth. It is the driver of the plate tectonics of the crust as is discussed in IAL 11: The Earth.
- in the Earth's atmosphere.
-
Question: What is a common, everyday, obvious example of
convection?
- The freezing of water.
- The boiling of water.
- The churning of butter.
Answer 2 is right.Boiling is actually the formation of bubbles of gas throughout a liquid and does NOT necessarily involve convection. But when water boils convection is usually also happening.
-
Question: Why can't convection
happen in truly rigid solids?
- The parts of the solid arn't free to move relative to each other.
- There are no heat flows through solids.
- Solids are perfect insulators.
Answer 1 is right.Answer 3 is wrong, but if true, implies answer 2, but answer 2 does NOT imply answer 3 since there could be no heat flows in solids for other reasons. Just a little exercise in logic.
The full calculation requires 3-dimensional hydrodynamics dynamics which is still difficult even with supercomputers. Frequently, one gets the wrong answer.
Dealing with convection is one of the difficult and uncertain parts of astrophysics. For example, our understanding of stellar evolution is we think quite good, but uncertainty about convection is one of the weak links.
The figure below (local link / general link: star_convection.html) illustrates convection in stars as a function of stellar mass.
Remember radiative transfer happens in convective zones too: it is just NOT the dominant heat transport mechanism there.
In the Sun, the convective zone extends from about 0.71 R_☉ to the photosphere (Cox-342).
In the Sun, we actually see the tops of the CONVECTION CELLS. They are the solar granules. See the figure below (local link / general link: sunspots_intro.html).
- Convection Redux:
Recall a basic fact of thermodynamics: 2nd law of thermodynamics which requires entropy increase to a maximum for a closed system.
Why this is so can be understood at the microscopic level, but we'll give it a pass.
The interiors of stars are hot because of nuclear burning brought about by high temperature (initially due to stellar contraction and later due to nuclear burning itself) and high density due to gravity and the huge mass of stars.
The stars actually have low entropy because they have so much compacted heat energy: i.e., highly ordered heat energy.
But space has very high entropy because of its low density.
The overall entropy of stars and space is increased by spreading out of the heat energy of the stars throughout space.
The stars emit EMR to do this.
In fact, according to our current understanding of cosmology, the stars will never succeed in heating space up.
There may be a very cold thermodynamic equilibrium in of order 10**100 years, but that is a very speculative extrapolation of what we know today (HI-477). This future is discussed in IAL 30: Cosmology.
-
Brown dwarfs
are substellar objects
which we explicate
in the figure below
(local link /
general link: brown_dwarf_comparison.html).
- observation.
- modeling.
Note that NEITHER observations NOR modeling definitive yet by any means.
Question: The discussion of
brown dwarfs
in the figure above
(local link /
general link: brown_dwarf_comparison.html)
is based on:
Both answers are right.
-
Stars do evolve on the
main sequence.
- Its carbon is being converted to diamond.
- Its core hydrogen is being converted to helium.
- Its surface hydrogen is being converted to helium.
- For Example, the Sun:
For example of main-sequence stellar evolution, let us consider the main-sequence stellar evolution Sun as illustrated in the figure below.
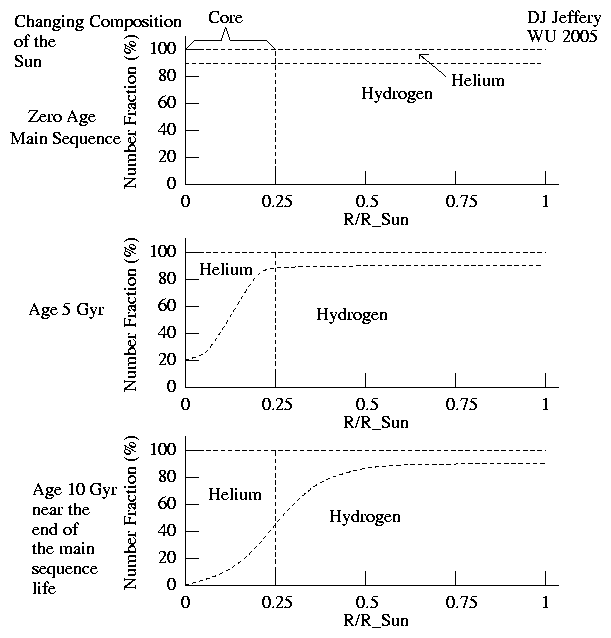
Caption: A cartoon of the evolving composition of the Sun (CM-315).
Credit/Permission: © David Jeffery, 2005 / Own work. Image link: Itself.
The decrease in hydrogen fuel in the core has the seemingly paradoxical result that stars will get more luminous over their main sequence life:
- Pressure support depends on the number of particles for
ordinary gases. In fact, pressure is linearly proportional
to the number of particles.
- When hydrogen is fused to helium,
4 particles are converted to 1.
- This causes a tendency to loss in pressure
which in turn causes a tendency to contraction
due the gravitational force on the Sun's
own mass.
- But contraction increases the core density and
increases the temperature essentially due to gravitational potential
energy being converted into thermal energy.
- The higher density and temperature, the higher the pressure
and thus collapse is resisted.
- But higher density and temperature tend to increase the
collision rate of hydrogens and other isotopes in
hydrogen burning chains, and thus the hydrogen burning rate.
- This tendency more than compensates for the decrease in fuel innermost core,
and so there is a higher rate of energy production
and the star gets brighter.
Note there is lots of hydrogen in the outer parts of the core.
- The upshot is that
main sequence stars
burn brighter as they exhaust their fuel.
The extra energy tends to make the outer layers expand: so as the core gets denser, the star actually tends to increase in size.
Stars larger than about 1 M_☉ get a little cooler on the surface during main sequence evolution. Since they are getting brighter too, they move upward and rightward on an HR diagram (CK-314).
The Sun and smaller stars??? will actually get slightly hotter on the surface for awhile anyway (FK-467). They would move upward and/or to the left on the HR diagram. See the figure below (local link / general link: star_hr_named_stars_cartoon.html).
-
These results for
main-sequence
stellar evolution
are probably only
understood in a computer modeling sense. This means
we put the right physical ingredients in a computer model and
we get the results. The results defy any simple explanation.
A lack of simple explanation is often the case in computer calculations: we simply say we understand in a computer modeling sense.
The Sun is now about 30 % brighter than when initially on the main sequence about 4.6 Gyr ago.
It will be about 30 % brighter than now in about 3.5 Gyr (WB-106; FK-493)
This gradual brightening of the Sun is known only theoretically. But we think we understand main sequence stars well in their main behavior.
So the brightening is about as certain a result as a purely theoretical result can be.
The brightening is a pretty modest change for the Sun.
But it probably means the doom of complex life on Earth within of order a gigayear or two by first eliminating the carbon dioxide from the atmosphere and then eliminating liquid water.
-
Well one might imagine that life evolves in a way to
overcome its current physical limitations, and endure
or modify the brute physical changes that are coming.
But that's more than physical science can know.
The brightening of the Sun is further explicated in the figure below (local link / general link: sun_evolution.html).
- Main-Sequence Lifetimes:
The main sequence lifetime of a star begins when the star settles on the zero-age main sequence on the HR diagram???? (CK-304).
It ends when the star's core hydrogen is sufficiently exhausted for the burning rate in the core to slow down or, more loosely, when the core hydrogen is exhausted (CK-311).
-
Question: How does
main sequence lifetime vary with
star mass?
- It increases with mass.
- It stays constant with mass.
- It decreases with mass.
Answer 3 is right.The lifetimes fall very quickly with mass in fact:
lifetime t ≅ constant/M**(2.5) .
This is a faster decrease than an inverse-square law decrease illustrated in the figure (local link / general link: function_behaviors_plot.html).
-
We discuss the
Λ-CDM model
in
IAL 30: Cosmology.
-
Question: Given the
age of the observable universe = 13.797(23) Gyr (Planck 2018),
are there star types none of whose members have ever
left the main sequence?
- No.
- Yes. All stars born less than ⪅ 0.9 M_☉ are still on the main sequence.
Answer 2 is right.- Ages of Stars on the Main Sequence:
We know the duration of main-sequence lifetimes from computer simulations to relatively high accuracy/precision nowadays.
But how do we know the ages of observed main sequence stars?
In general, we CANNOT. But we can if the main sequence stars are in star clusters.
The method of determining the ages of main sequence stars in star clusters by means of Hertzsprung-Russell (HR) diagrams and turn-offs is explicated in the figure below (local link / general link: star_hr_turn_off.html).
- Stars with Stellar Mass Less Than 0.9 M_☉:
If we look again at the table of approximate main-sequence lifetimes (see below), we that some low-mass stars will be on the main sequence for hundreds of gigayears.
The fate of very low-mass stars (and also stars of mass up to about 8 M_☉) is to become white dwarfs whose nature is discussed in IAL 24: Compact Remnants: White Dwarfs and Neutron Stars.
Here will just say white dwarfs are star-mass objects of Earth-size (and thus very dense) that are NOT burning any nuclear fuel and are just cooling off forever.
-
White dwarfs
exist, of course: there are just none that originated from
stars of less than about 0.75 M_☉ when on the
main sequence.
But it is is probably a comparatively gentle process??? particularly for red dwarfs which are main sequence stars in the mass range 0.08--0.4 M_☉ (CK-311).
Red dwarfs are convective throughout and will convert almost all there hydrogen to helium.
They will never burn helium unlike more massive stars, and so should just contract probably pretty slowly into white dwarfs.
They probably will just cool in the post-main-sequence phase (CK-311), but since contraction causes heating they might heat up for awhile???? but I've NOT been able to find out for sure.
IAL 23: Late Star Evolution and Star Death takes up the subject of the post-main-sequence evolution of stars of about solar mass and larger.
- Pressure support depends on the number of particles for
ordinary gases. In fact, pressure is linearly proportional
to the number of particles.
-
Question: What obvious change must a star be undergoing
even during its slow main sequence lifetime?
Answer 2 is right.
The surface is much too cool and rarefied for hydrogen burning.
-
As preview of the
post-main-sequence evolution
of stars
(which is more fully explicated in
IAL 23: The Post-Main-Sequence Life of Stars),
see the two
Hertzsprung-Russell (HR) diagrams
in the two figures below
(local link /
general link: star_hr_post_main_sequence.html;
local link /
general link: sun_evolution_hr.html).
Form groups of 2 or 3---NOT more---and tackle
Homework 22
problems 25--33 on
main sequence stars,
red dwarfs,
and
brown dwarfs.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 22.
Group Activity: