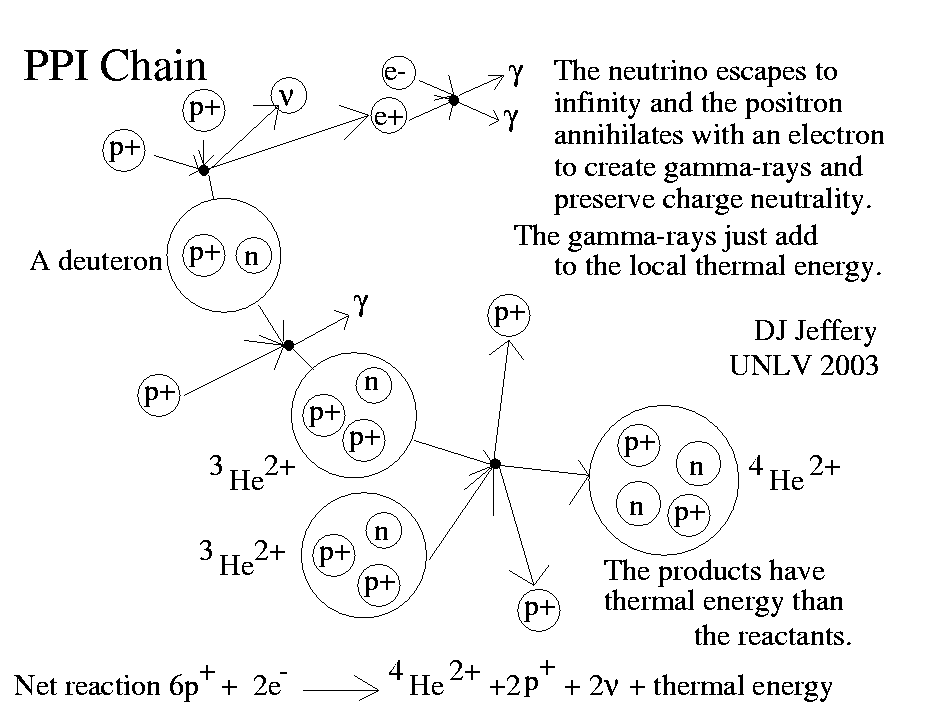
Caption: The proton-proton chain in the pp I branch.

Features:

1. The dominant hydrogen burning (i.e., H-to-He-4 burning) process in stars less than ∼ 1.5 M_☉ (e.g., the Sun) is the proton-proton chain reaction (HI-343; Cl-369) which comes in three versions the pp I branch, the pp II branch, and the pp III branch. The pp I branch and pp II branch are dominant in the Sun.

2. The pp I branch is illustrated in the diagram.

   It includes binding nuclear reactions due to the strong nuclear force and beta decays (which transform protons into neutrons or vice versa) due to the weak nuclear force.

   
   
   
   
   The net pp I branch nuclear reaction formula is

     6p(+) + 2e(-) → He-4(2+) + 2p(+) + 2ν + 26.20 MeV 
     or
     4p(+) + 2e(-) → He-4(2+) + 2ν + 26.20 MeV     , 

   where p(+) is a proton, e(-) is an electron, He-4(2+) is the helium-4 (He-4) nucleus (i.e., doubly ionized He-4), ν is a electron neutrino, and 26.20 MeV is the heat energy released (Wikipedia: Proton-proton chain: Energy release). Note, we do NOT count the 0.53 MeV energy of the electron neutrinos since they escape to infinity and do NOT contribute to the heat energy in the star (Wikipedia: Proton-proton chain: Energy release).

   Since the heat energy released is positive, the net pp I branch nuclear reaction is an exothermic reaction as it must be for the pp I branch to help power the star.

3. In fact, the rate-determining step of the proton-proton chain reaction is the first one: the p-p reaction. This is because it relies on the weak nuclear force to transforms one proton into a neutron (n) with the ejection of a positron (e+) and an electron neutrino (ν_e) (see Wikipedia: Proton-proton chain reaction: The proton-proton chain reaction). The slowness of p-p reaction is why stars less massive than ∼ 1.3 M_☉ (see Wikipedia: Proton-proton (pp) chain reaction) stay on the main sequence as long as they do: i.e., ⪆ 3 Gyr (see Table: Representative lifetimes of stars as a function of their masses).

   For more details on the p-p reaction, see nuclear_burning_pp.html.

4. See Proton-proton chain reaction keywords below (local link / general link: nuclear_burning_ppi_chain_keywords.html):

   EOF

5. Note, as in all important nuclear burning processes for energy generation in stars, all the nuclear reactions have to be binary: i.e., one particle with one particle.

   Three-particle nuclear reactions are very rare and are unimportant---higher combination nuclear reactions are even more rare and more unimportant.

6. For hydrogen burning (i.e., H-to-He-4 burning), the rest mass of the products is 0.7 % less than the rest mass of the reactants (CK-262).

   Now rest mass is a form of energy and energy is conserved overall (see Wikipedia: Conservation of energy).

   The missing rest mass was transformed into the emitted heat energy (i.e., primarily kinetic energy of the products and electromagnetic radiation (EMR)).

   Note, the lost rest mass is also counted as released nuclear binding energy. Remember that energy categories often overlap.

7. Recall E=mc**2, and thus 1 kilogram of rest mass in energy terms (or mass-energy terms) is

     1 kg * (3*10**8 m/s)**2
     = 9*10**16 joules
     = about 2.5*10**10 KW-hours ( 1 kW-hr = 3.6*10**6 J )
     = about 20 megatons of TNT ( 1 megaton TNT = 4.184*10**15 J )  .  

   Note it is the chemical energy of TNT that is meant by 1 megaton of TNT (see Wikipedia: TNT equivalent). This chemical energy is converted into the energy of explosion: i.e., thermodynamic work which is primarily in the form of macroscopic kinetic energy for some time period.