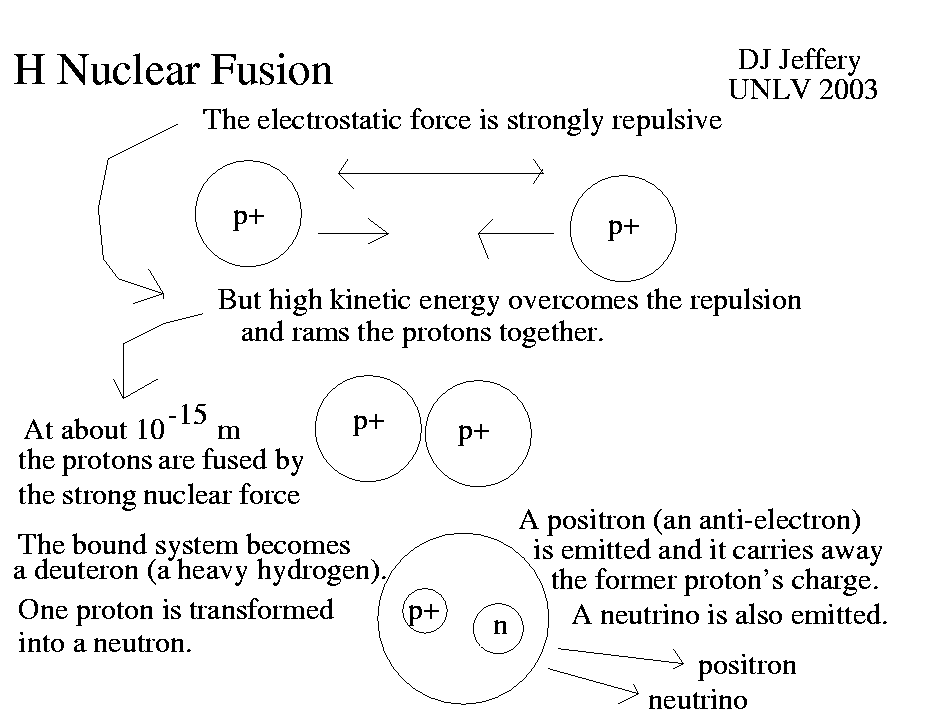
Caption: Protons (p+) (i.e., Hydrogen (H-1) nuclei) undergoing nuclear fusion to create a deuteron (D,H-2): i.e., the p-p reaction.

Features:

1. Protons strongly repel each other due to the electrostatic force (AKA Coulomb's law force).

2. Under the high temperature and density conditions in the cores of stars, 2 protons are sometimes rammed close enough against the electrostatic force to allow the short-range strong nuclear force to turn on and marginally??? bind them.

   Note that the strong nuclear force only extends to ∼ 1 fermi (fm) = 10**(-5) Å = 10**(-15) m.

3. The nearly bonded 2 protons form a highly unstable He-2 (diproton) which rapidly either unbinds???? or rarely???? undergoes a beta decay (due to the weak nuclear force) which transforms one proton into a neutron (n) and ejects a positron (e+) and an electron neutrino (ν_e) (see Wikipedia: Proton-proton chain reaction: The proton-proton chain reaction).

   The proton and neutron form a stable deuteron (D,H-2). The complete reaction is the p-p reaction itself.

   The fact that the transformation of a He-2 to a deuteron is rare makes the p-p reaction to form deuterons a very slow process in the overall proton-proton (pp) chain reaction process and, in fact, the rate-determining step. That the p-p reaction is so slow is why stars less massive than ∼ 1.3 M_☉ (see Wikipedia: Proton-proton (pp) chain reaction) stay on the main sequence as long as they do: i.e., >∼ 3 Gyr. But stars that use CNO cycle as their main hydrogen burning process (i.e., those with stellar mass >∼ 1.3 M_☉) have much shorter main-sequence lifetimes: e.g., <∼ 370 Myr for stars of >∼ 3 M_☉. See Table: Representative lifetimes of stars as a function of their masses.

   In nuclear reaction formulae terms, the nuclear reactions are

     p + p → He-2
     He-2  → H-2 + (e+) + ν_e
   
     with summed nuclear reaction formula
   
     p + p → H-2 + (e+) + ν_e  
   
     but then counting the positron (e+) annihilation,
     one gets the net nuclear reaction formula
   
     p + p + e- → H-2 +  ν_e  + 1.442 MeV .  

4. Note that the positron (e+) carries away a positive elementary charge (e), and thus maintains charge conservation which is believed to be an unbreakable conservation law. In stars and probably all elsewheres, the positron will usually rapidly meet up with an electron (its antiparticle) and said meeting (which often leads to binding to form a positronium briefly) will lead to pair annihilation which produces 2 or 3 gamma rays with net energy 1.022 MeV (see Wikipedia: Annihilation: Electron-positron annihilation). In the deep interior of stars, the gamma rays are counted as heat energy. The rest of the 1.442 MeV in the net nuclear reaction formula is the kinetic energy of the resultants the deuteron and positron---they are kicked apart---which is also counted as heat energy in the deep interior of stars.

   The fact that heat energy is emitted means the nuclear reaction is an exothermic reaction.

   The electron neutrino (which is a highly unreactive elementary particle) usually escapes to infinity and never interacts with anything again for a quasi eternity. Its energy (kinetic energy and rest mass energy) are lost to the star and is NOT counted as heat energy in the star (i.e., it is NOT included in the 1.442 MeV yours truly thinks though there is unclearness in Wikipedia: Proton-proton chain: The proton-proton chain).

5. See Proton-proton chain reaction keywords below (local link / general link: nuclear_burning_ppi_chain_keywords.html):

   EOF