Image 1 Caption: Hydrostatic equilibrium illustrated for a plane-parallel system of a fluid in a gravitational field.

Features:

Hydrostatic equilibrium is when a fluid is at rest everywhere because everywhere the forces are balanced.
Gravity and the pressure force are usually the forces.
For the diagram, Newton's 2nd law of motion (AKA F=ma) specializes to
ma = 0 = -mg + (p_1-p_2)*A ,
where acceleration a = 0 because of the constraint of hydrostatic equilibrium, A is the area of planar layer, m is the mass of the planar layer, -g is the gravitational field and g is positive, p_1 is the pressure below the layer, p_2 is the pressure above the layer, and we take up as positive.
Note p_1 > p_2 for hydrostatic equilibrium.
Another perspective is that p_1*A must equal the gravitational force on all the mass above the lower layer.
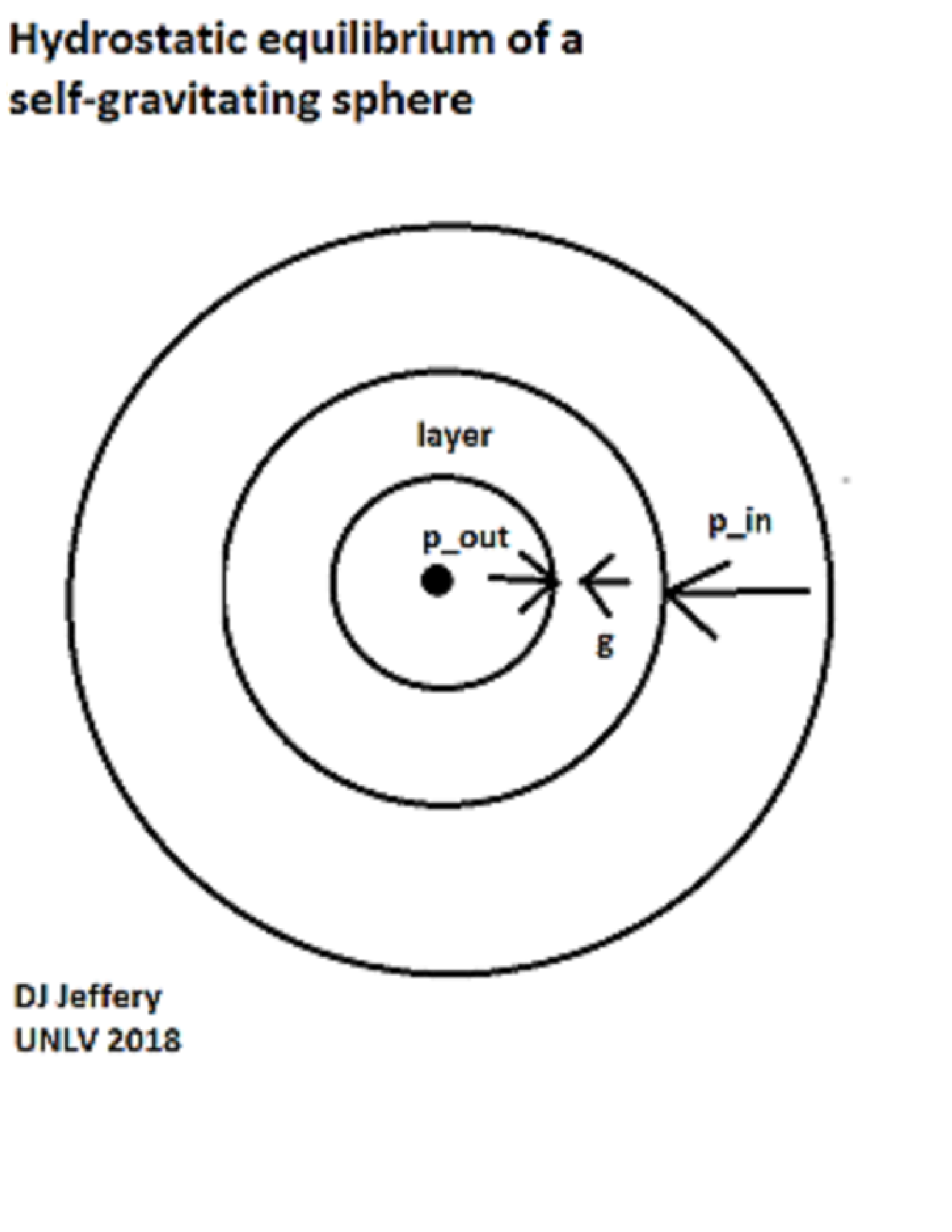
Image 2 Caption: The spherically-symmetric hydrostatic equilibrium case.
Note in both plane-parallel and spherically-symmetric hydrostatic equilibrium cases that in the directions perpendicular to the gravitational force, the pressure must be constant or there would be motion and NOT hydrostatic equilibrium.
To generalize to the spherically-symmetric hydrostatic equilibrium case the result we stated above, in all spherically-symmetric hydrostatic self-gravitating pressure-supported bodies, the upward pressure force of every layer must balance the gravitational force on all the mass above that layer. For example, this is true for the Earth's atmosphere and the Earth's interior. To generalize, it is true for moons, planets, and stars. Corrections do have to be made for deviations from spherical symmetry, of course.
For spherically-symmetric astro-bodies, the hydrostatic equilibrium equation (a differential equation) is
```
  (dp/dr) = -Gm(r)ρ(r)/r**2  ,
 
    where dp/dr is the rate of change 
            of pressure with radius,
          p(r) is pressure,
          ρ(r) is the density
            as a function,
          gravitational constant 
            G = 6.67430(15)*10**(-11) (MKS units),
          and r is radius.
```
Like all differential equations, the hydrostatic equilibrium equation tells you what is true at every point in a spherically-symmetric structure, but it does NOT tell you what density and pressure are at every point.
You have to solve for them which usually requires a computer calculation.
The hydrostatic equilibrium equation is one of 4 equations of stellar structure.
The 4 equations of stellar structure are the equations that are solved to obtain a stellar structure model, a hydrostatic model that is. Stars undergoing large-scale motions require hydrodynamic modeling which is much more difficult and less certain.

Images:

Credit/Permission: David Bailey (AKA User:H2g2bob), 2006 (uploaded to Wikimedia Commons by User:Stannered, 2008) / Public domain.
Image link: Wikimedia Commons: File:Hydrostatic equilibrium.svg.
Local file: local link: hydrostatic_equilibrium.html.

Fluids file

hydrostatic_equilibrium.html

ma = 0 = -mg + (p_1-p_2)*A ,