Image 1 Caption: The pressure curves of the classical ideal gas (see also Wikipedia: Ideal gas law) and ideal quantum gases (i.e., the Fermi gas and the Bose gas) as functions of temperature (i.e., Kelvin temperature) for a fixed particle density. The ideal gases are for the case of non-relativistic limit (i.e., they are consist of massive particles moving at velocities asymptotically close to zero relative to the vacuum light speed c = 2.99792458*10**8 m/s ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns) in (3-dimensional physical) space.

"The plot has been scaled in a way that the free particle degeneracy factors, densities, masses, etc. are all factored out and irrelevant." (Slightly edited.)

Features:

The gases:
1. A classical ideal gas consists of classical free particles (i.e., they obey classical physics). Classical free particles obey Maxwell-Boltzmann statistics and the Maxwell-Boltzmann distribution. In fact, all free particles are always really quantum free particles, but they behave as classical free particles in the low-density, low-velocity asymptotic limit.
2. A Fermi gas consists of fermions which are quantum mechanical particles that obey Fermi-Dirac statics and have half-integer spin: i.e., 1/2, 3/2, 5/2, ...
3. A Bose gas consists of bosons which are quantum mechanical particles that obey Bose-Einstein statistics and have integer spin: i.e., 0, 1, 2, ...
All the gases have an equation of state (EOS): i.e., a formula relating thermodynamic variables. Almost always by equation of state (EOS), one means a pressure law.
The
classical ideal gas pressure P = (N/V)kT ,
where N is particle number, V is volume, the Boltzmann contant k = 1.380649*10**(-23) J/K = (8.617333262...)*10**(-5) eV/K (exact) ≅ 10**(-4) eV/K ≅ 10**(-10) MeV/K, and the slope is Nk/V (when P is plotted as function of temperature).
This pressure law is usually known as the ideal gas law P = (N/V)kT.
The ideal gas law is probably the simplest of all laws relating thermodynamic variables: i.e., equations of state (EOS).
The ideal gas law is often an excellent emergent theory: i.e., it is an exact limiting behavior that is so closely approached by actual gases in the right limit that in many cases discrepancies are unobservably small. Of course, we need other pressure laws where the ideal gas law fails: for example and most importantly, those for the Fermi gas and the Bose gas.
We will NOT display the formulae for pressure laws for the Fermi gas and the Bose gas (except for the extreme relativistic photon Bose gas whose pressure law we show below in discussing Image 3). However, as Image 1 shows, as temperature increases, the Fermi gas and the Bose gas both approach the classical ideal gas pressure law asymptotically in slope though with a vertical offset??? that is usually immeasurably small for everyday life conditions. Note there is an important exception, free electrons in metals (ordinary usage) approximate a Fermi gas when the metals (ordinary usage) are solid or liquid.
The pressure of Fermi gas / Bose gas for the case illustrate in Image 1 is always higher/lower than that of classical ideal gas due the exchange interaction which is a purely quantum mechanical effect, and so NOT derivable from classical physics.
The discrepancy from ideal gas law P = (N/V)kT is negligible for sufficiently high temperature.
For the Fermi gas, the temperature labeled T_F on Image 1 is called the Fermi temperature: it is the characteristic temperature for the transition from the region of degeneracy pressure (which is largely independent of temperature) to the region where the Fermi gas asymptotically (in slope) approaches the ideal gas law P = (N/V)k/T.
Note the degeneracy pressure is nonzero at absolute zero T = 0 K.
Note absolute zero T = 0 K case is an ideal limit that CANNOT be reached practically---but it can be approached very closely experimentally and in some astrophysical systems.
For Bose gas, the temperature labeled T_B and marked by the ★ symbol in Image 1 is called the Bose-Einstein condensate critical temperature. Going below this temperature, the pressure drops rapidly as more and more bosons (i.e., particles obeying Bose-Einstein statistics) are absorbed into the Bose-Einstein condensate. The Bose-Einstein condensate critical temperature is also the characteristic temperature for the transition to the higher temperature region where the Bose gas asymptotically (in slope) approaches the ideal gas law P = (N/V)kT.
We will NOT describe the Bose-Einstein condensate here, but we note that as the pressure asymptotically goes to zero as temperature goes to absolute zero T = 0 K.
At absolute zero T = 0 K, all the bosons are in the Bose-Einstein condensate.????
Note again, absolute zero T = 0 K case is an ideal limit that CANNOT be reached practically---but it can be approached very closely experimentally and in some astrophysical systems.
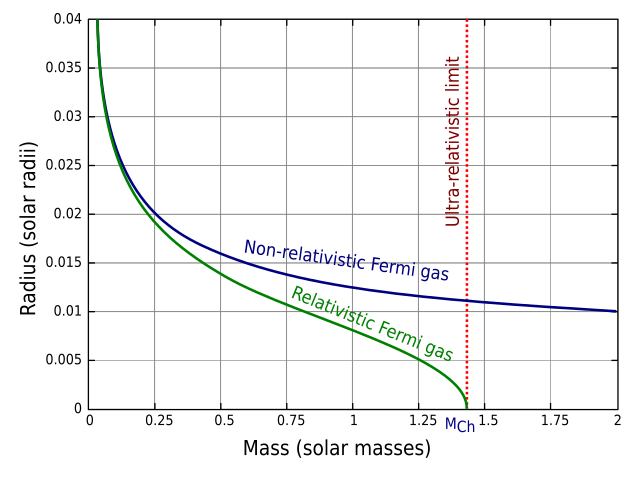
Image 2 Caption: The mass-radius relationship for a fiducial white dwarf modeled with an absolute zero (i.e., T=0 K) Fermi gas pressure.
For more on white dwarf pressure law, see White dwarf file: white_dwarf_mass_radius_relation.html.
White dwarfs are compact remnants of stars after their main-sequence lifetime and post-main-sequence lifetime. They are typically of order 0.6 M_☉ (Wikipedia: White dwarf: Composition and structure) and 1 Earth radius ≅ 0.01 solar radii. Known white dwarfs estimated span a mass range 0.17 to 1.33 M_☉.
Note the Earth equatorial radius R_eq_⊕ = 6378.1370 km and solar radius R_☉ = 6.957*10**5 km = 109.1 R_eq_⊕ = 4.650*10**(-3) AU.
White dwarfs have NO nuclear burning and just cool off very slowly forever. However, there none with photospheric temperature less than ∼ 4000 K (Wikipedia: White_dwarf: Radiation and cooling). None have been able to get cooler within the age of the observable universe = 13.797(23) Gyr (Planck 2018).
White dwarfs are held up against collapse under self-gravity by degenerate electron gas pressure (i.e., the degeneracy pressure of a Fermi gas of electrons with temperature below or of order the Fermi temperature). Since degeneracy pressure is largely independent of temperature, white dwarfs are sustained against collapse even in the limit of absolute zero (i.e., T=0 K).
Image 2 shows 2 curves for the limit of absolute zero (i.e., T=0 K) for idealized white dwarfs. The relativistic case approximates real white dwarfs. Note radius decreases with mass.
The relativistic case gives an upper limit mass where the radius goes to zero. This upper limit mass is called the Chandrasekhar mass. For the ideal case, the formula for the Chandrasekhar mass is
```
  
  M_ch = (1.45620...  M_☉)/[(μ_e/2)**2]  
```
(Wikipedia: Chandrasekhar limit: Physics), where μ_e is the mean molecular mass per electron which approximately obeys the formula
```
  
  μ_e ≅ 2/(1+X)  , 
```
where X is the mass fraction of hydrogen (H, Z=1) (e.g., Cl-84). For white dwarfs, X ≅ 0.
In fact, for real white dwarfs X is NOT exactly zero, the μ_e needs a better calculation in any case, temperature is above absolute zero (i.e., T=0 K), rotation effects need to be considered, and general relativitic effects (NOT included in the given formula for the Chandrasekhar mass) need to be considered. Nevertheless, the Chandrasekhar mass for real white dwarfs is usually ∼ 1.4 M_☉.
A white dwarf can be driven toward the Chandrasekhar mass by mass accretion from a close binary companion. What happens as such a white dwarf approaches the Chandrasekhar mass? If its composition is mainly carbon (C,Z=6) and oxygen (O,Z=8) (which is one the two main possibilities), its central density can become so high that there is thermonuclear runaway leading to a Type Ia supernovae (SNe Ia) which totally disrupts the white dwarf giving an expanding supernova remnant and leaving NO compact remnant. However, if its composition is mainly oxygen (O,Z=8), neon (Ne,Z=10), and magnesium (Mg,Z=12) (which is the other of the two main possibilities), the white dwarf will collapse to a neutron star.
Why a neutron star NOT a black hole for white dwarf collapse?
The failure degenerate electron gas pressure at the Chandrasekhar mass leads to a collapse in which the electrons and protons combine to make neutrons which have the degenerate neutron gas pressure. This pressure will sustain the collapsing white dwarf as a neutron star (typical radius 10 km, typical mass 1.4 M_☉).
In fact, neutron stars mostly form from core collapse supernovae which form from stars of the mass 8 M_☉ to of order 20 M_☉ on the main sequence and NOT from collapsing white dwarfs (which happen rarely).
Actually, neutron stars have an upper mass the Tolman-Oppenheimer-Volkoff mass which is analogous to the Chandrasekhar mass. The value of the Tolman-Oppenheimer-Volkoff mass is thought to be in the range 2 to 3 M_☉. The uncertainty in the value is due to uncertainty in the nuclear matter equation of state (EOS) and the uncertainty in observational constraints.
If a neutron star undergoes mass accretion from a close binary companion and reaches the Tolman-Oppenheimer-Volkoff mass, it will collapse to being a stellar mass black hole. In fact, stellar mass black holes mostly form from core collapse supernovae which form from stars of ⪆ of order 20 M_☉ on the main sequence and NOT from collapsing neutron stars due mass accretion (which happen rarely). Many stellar mass black holes probably form from neutron star mergers. The neutron star mergers usually occur for neutron star binary systems that inspiral to merger by losing orbital energy in the form of gravitational waves.
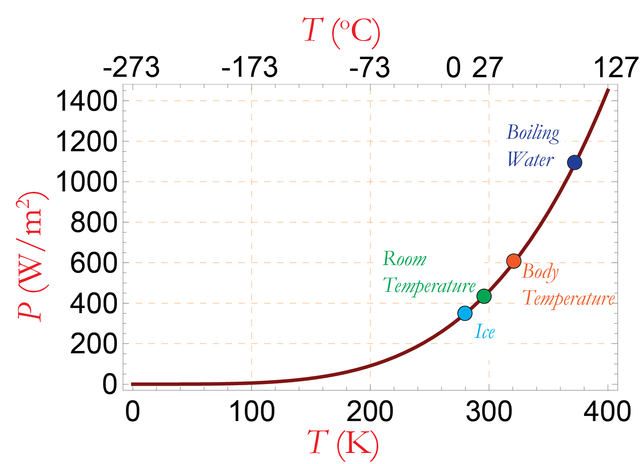
Image 3 Caption: A plot of the Stefan-Boltzmann law which gives the wavelength-integrated flux radiated from the surface of a blackbody radiator.
The vertical axis is labeled P for power, but F for flux is choice of yours truly.
Yours truly uses P for pressure in this figure.
But to flux is proportional to the pressure of the photon gas that makes up the flux: i.e.,
P ∝ F .
The Stefan-Boltzmann law is
F = σT⁴ ,
where F is flux in units of watts (i.e., joules per second) per meter squared, the Stefan-Boltzmann constant σ = (5.67037441918442...)*10**(-8) W/*m**2/K**4 (exact) (see NIST: Fundamental Physical Constants --- Complete Listing 2018 CODATA adjustment), and T is temperature on the Kelvin scale.
In fact, blackbody radiation is a Bose gas where the bosons are photons.
However, it is DISTINCT from the Bose gas shown in Image 1. That Bose gas is for non-relativistic massive particles.
Photons are massless particles that always move at the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns, and so are always extremely relativistic. Being massless particles implies an infinite Bose-Einstein condensate critical temperature. The upshot is that blackbody radiation NEVER behaves like an classical ideal gas as the Bose gas in Image 1 does asymptotically as temperature grows large.
The pressure law for blackbody radiation (i.e., blackbody radiation pressure) is
P = (1/3)aT⁴ ,
where radiation constant a = (4σ/c) = (7.56573325028000...)*10**(-16) J/*m**3/K**4 (exact) (see also Wikipedia: Photon gas: Thermodynamics of a black body photon gas; Hyperphysics: Radiation Energy Density).
Thus, blackbody radiation pressure grows as T**4, and so is proportional to the Stefan-Boltzmann law flux shown in Image 3 (as mentioned above), where the vertical axis should be F for flux to be consistent with this figure.
Blackbody radiation pressure and other types of radiation pressure are important in many astronomical system.
For important example, blackbody radiation pressure is important in massive stars where it adds to the ideal gas law pressure provided by baryonic matter (with usually approximately the cosmic composition: hydrogen (H, Z=1) ∼ 73 %, helium-4 (He-4, Z=2) ∼ 25 %, metals of order 2 %). To illustrate this:
1. For solar mass main-sequence stars, it is nearly negligible.
2. For main-sequence stars of order 20 M_☉, it is of order 10 % of the central pressure. Note this is a crude estimate from Clayton (1983, p. 164).
3. For main-sequence stars of order 150 M_☉, it is of order 50 % of the central pressure. Note this is a crude estimate from Clayton (1983, p. 164).
Donald Clayton (1983, p. 155--165) and Phil Armitage (2003) give introductions to the basics of pressure in stars.

Images:

Credit/Permission: User:Nanite, 2020 / Public domain.
Image link: Wikimedia Commons: File:Quantum ideal gas pressure 3d.svg.
Credit/Permission: User:AllenMcC, User:Chrkl 2007 / Public domain.
Image link: Wikimedia Commons: File:ChandrasekharLimitGraph.svg.
Credit/Permission: © USER:LVD, 2014 / CC BY-SA 3.0.
Image link: Wikimedia Commons: File:Emissive Power.png.

local link: gas_classical_quantum.html

Thermodynamics file

gas_classical_quantum.html

classical ideal gas pressure P = (N/V)kT ,

P ∝ F .

F = σT4 ,

P = (1/3)aT4 ,

F = σT⁴ ,

P = (1/3)aT⁴ ,