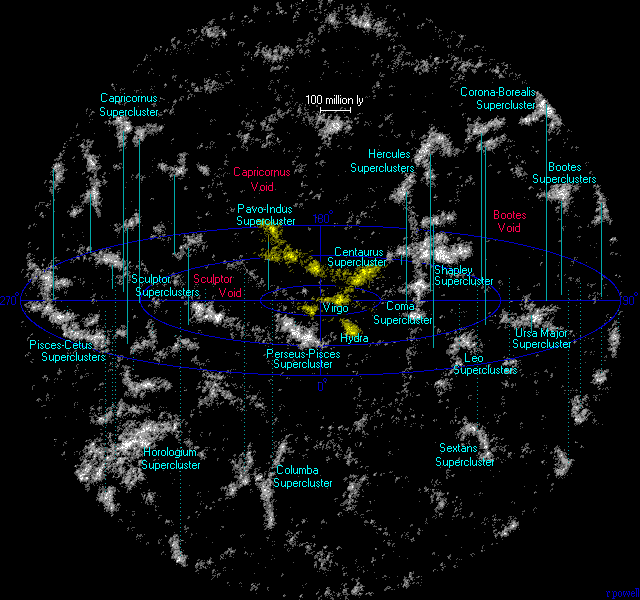
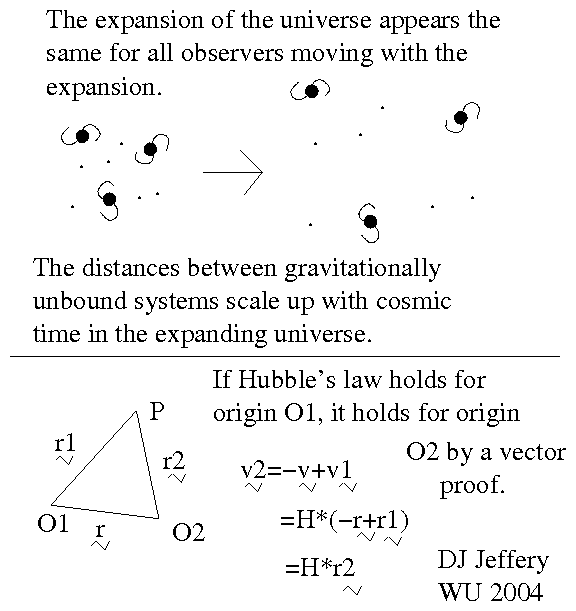Features Extended:

Celestial Frames:

A celestial frame (which is a term invented by yours truly) is a special case of center-of-mass (CM) inertial frames (which is another term invented by yours truly: see Mechanics file: frame_basics.html: Center-of-Mass (CM) Inertial Frames).
Celestial frames are reference frames used to describe systems of astro-bodies with approximations that usually excellent for such systems. Celestial frames are used all the time in celestial mechanics without apparently having their own name. Since it is very inconvenient NOT to have a name, yours truly invented the term celestial frame.
As yours truly uses the term celestial frames, the approximations are that celestial frames are limited to Newtonian physics (except sometimes for approximations to relativistic physics: i.e., combined special relativity (1905) general relativity (1915)) and that compact astro-bodies (e.g., moons, asteroids, planets, stars, and compact remnants (white dwarfs, neutron stars, black holes)) are treated as point masses.
Note:
1. Computer simulations can be done with relativistic physics, but they are vastly more computationally expensive than Newtonian physics computer simulations, and so are only done when needed.
  In fact, celestial frames and CM inertial frames can only be extended over a relatively small region of the observable universe: for about how far, see the below section Comoving Frames. They emerge locally in a full relativistic physics calculation: i.e., they are NOT imposed as an approximation (which can be an excellent approximation) for doing a Newtonian physics calculation
2. The INTERNAL motions of a compact astro-body are overwhelmingly best treated using a CM inertial frame just for that compact astro-body, and so are NOT treated in celestial frames. This is because the computational domain of compact astro-bodies is usually cleanly separable from the computational domain outside of them. In fact, compact astro-bodies usually require a rotating frame converted into an inertial frame using inertial forces: i.e., the centrifugal force, the Coriolis force, and the Euler force. Rotating frames are NEVER needed for the realm needing celestial frames (as yours truly truly uses the term).
3. Neutron stars and black holes always require a treatment using general relativity: Newtonian physics is inadequate for them, and therefore so CM inertial frames used for them need some sort of extension beyond Newtonian physics.
4. Celestial frames with only point masses are used in traditional celestial mechanics.
Note the term celestial frame can be used as a synonym for the system of astro-bodies for which the celestial frame is defined. Context as usual determines the meaning of celestial frame.
To explicate celestial frames:
The center of mass of a system of astro-bodies is the origin for celestial frame. The celestial frame is described by a coordinate system extending from the center of mass. The celestial frame and therefore its coordinate system are NOT in rotation relative to the observable universe (i.e., the bulk mass-energy of observable universe). This means the celestial frame is NOT a rotating frame, and does NOT need any of the rotating frame inertial forces: i.e., the centrifugal force, the Coriolis force, and the Euler force.
Usually, the main forces that act on the system are gravity, the tidal force, and the cosmological constant force (or its dark energy equivalent whatever that is).
However, gas pressure and the magnetic can be important in some applications. An important one for gas pressure is structure formation (AKA large-scale structure formation) beyond the approximation of only using point masses in what is called an N-body simulation. The electrostatic force (AKA Coulomb's law force) is probably NEVER important for the bulk motions of astro-bodies.
We have to make a distinction between INTERNAL and EXTERNAL forces on a celestial frame. The former partially determine the motions of the astro-bodies relative to the center of mass (i.e., the INTERNAL motions), but do NOT affect the center of mass motion at all relative to the outside world. The latter partially determine the INTERNAL motions and there NET force entirely determines the motion of center of mass relative to the outside world as dictated by Newton's 2nd law of motion. In fact, the center of mass motion must be determined relative to a larger celestial frame which incorporates the celestial frame we are describing.
Note:
1. The tidal force (which is only an EXTERNAL force) only affects the INTERNAL motions of the system. This is actually definitional: tidal force caused by the difference between the EXTERNAL gravitational field at any point in a celestial frame and the mass-weighted average of the EXTERNAL gravitational field on the celestial frame. If the EXTERNAL gravitational field is UNIFORM, the tidal force is zero.
2. The other forces can be both INTERNAL and EXTERNAL.
3. If the system is very low mass (e.g., spacecraft) the INTERNAL gravity will be negligible.
4. The cosmological constant force is very important for the overall expansion of the universe, but for most celestial frames, the INTERNAL cosmological constant force is negligible. Maybe only for celestial frames for large galaxies and galaxy clusters is somewhat significant.
5. In the Newtonian physics approximation which seems adequate almost always for the cosmological constant force, the INTERNAL cosmological constant force just pushes radially outward from the center of mass and the EXTERNAL cosmological constant force just pushes radially outward from center of mass of the aforementioned larger celestial frame which incorporates the celestial frame we are describing. The cosmological constant force is a rather strange force since it is just a general expansion force caused by physical space.
Celestial frames are, in fact, a way of dividing astro-bodies into systems that are useful (i.e., efficient) for analysis of their INTERNAL motions.
Note:
1. There is choice in defining celestial frames, but quite often the choice is obvious.
  Usually you choose celestial frames with the most UNIFORM EXTERNAL gravitational field all other things be equal in order to make the INTERNAL motions of the celestial frames more independent of the EXTERNAL environment (which may be poorly known) and therefore make the motions more easier to solve for.
2. To expand: When the INTERNAL gravitational forces of a system of astro-bodies are large relative to the EXTERNAL tidal forces caused by the EXTERNAL gravitational field, then the INTERNAL structure and motions are largely independent of the EXTERNAL gravitational field. However, the NET EXTERNAL force (due to the EXTERNAL gravitational field the EXTERNAL cosmological constant force, and the other EXTERNAL forces) always determine the motion of the center of mass of the system. But solving for the center of mass motion is a separate problem.
  The ideal celestial frame is one where the EXTERNAL gravitational field is UNIFORM over the celestial frame and the only other EXTERNAL force is the EXTERNAL cosmological constant force. In this case, the EXTERNAL gravitational field does NOT affect the INTERNAL motions at all: i.e., there is NO tidal forces. (The EXTERNAL cosmological constant force NEVER affects the INTERNAL motions as discussed above.) In particular, a perfectly UNIFORM EXTERNAL gravitational field CANNOT change the total angular momentum of celestial frame about the center of mass (CM): i.e., the celestial frame has conservation of angular momentum.
3. The ideal case actually virtually holds, for example, for most planetary systems and most multiple star systems. They are usually so small relatively that the EXTERNAL gravitational field is close to being UNIFORM over them, cosmological constant force as aforesaid has NO affect on INTERNAL motions, and other EXTERNAL forces are usually completely negligible.
Now relatively strong tidal forces tend to tear apart identifiable systems of astro-bodies.
So the ones that persist as identifiable systems (mostly because they are gravitationally bound) are those for which celestial frames are most useful for analysis.
Following from last point, the nested hierarchy of celestial frames used in astronomy mostly consists of identifable gravitationally-bound systems: i.e., planet-moon systems, planetary systems multiple star systems, star clusters (i.e., open clusters and globular clusters), galaxies, galaxy groups (which are just very poor galaxy clusters in yours truly's opinion), and galaxy clusters.
The nested hierarchy is illustrated in the cartoon (i.e., Image 1), but without comoving frames (which are NOT gravitationally-bound systems in an ordinary sense) as aforesaid in the preamble.
Note gravitationally-unbound systems smaller than the gravitationally-unbound galaxy superclusters (e.g., stellar associations) can also be incorporated in the nested hierarchy below the scale of comoving frames.
The interstellar medium (ISM) and intergalactic medium (IGM) (gravitationally-bound or NOT or mixed) which are often broken into nebulae or flows can also be incorporated in the nested hierarchy of celestial frames. However, they require hydrodynamics which we will NOT expand on here.
How far can you extend the use of a celestial frame using Newtonian physics?
Well, you have to keep the size less than the cosmological scale and small enough that the recession velocities (which are cosmological, NOT ordinary, velocities) of remote astro-bodies included in the celestial frame are much less than the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns.
If you try to extend to a celestial frame too far, you will have to use relativistic physics.

Comoving Frames:

Galaxy clusters are the largest gravitationally bound systems. The larger structures of the large-scale structure of the universe (AKA the cosmic web)---galaxy superclusters, galaxy filaments, and cosmic walls---are gravitationally unbound systems.
Note, however, there is NO absolute hard line between galaxy clusters and galaxy superclusters
In fact, identifying a structure of large-scale structure as a galaxy supercluster has generally been somewhat in the eye of the beholder: e.g., "It looks like galaxy supercluster to me."
In fact, galaxy superclusters are amorphous.
There is a precise procedure for defining galaxy superclusters, but it requires rather precise information about galaxy motions which may NOT be available any time soon for galaxies more than ∼ 100 Mpc from the Local Group (i.e., the galaxy group to which the Milky Way belongs). The precise procedure has been used to define the Laniakea Supercluster (which includes Local Group): see below Image 2 for the Laniakea Supercluster.
In fact, Image 2 can be used as an example of a comoving frame (though it is actually a bit small for comoving frame).
Comoving frames are the largest celestial frames.
How is a comoving frame specified?
A comoving frame can be defined at any point in space.
You just center on the point a large sphere which grows with the mean expansion of the universe: i.e., its radius scales up with the cosmic scale factor a(t), where t is cosmic time measured from the Big Bang singularity which was lookback time equal to the age of the universe = 13.799(21) Gyr.
The sphere is the comoving frame. Note the coordinate system for the comoving frame is NOT rotating relative to the observable universe just as for any other celestial frame.
And the center point of the sphere is the center of mass of the comoving frame.
The centers of mass of comoving frame participate in the mean expansion of the universe. Thus, the distances between the centers of mass scale with the cosmic scale factor a(t).
The comoving frame has to be large enough so that the interior obeys the cosmological principle: i.e., that the observable universe be homogeneous (same in all places) and isotropic (same in all directions) on a large enough scale.
Currently, for the local (and therefore modern) observable universe the scale is estimated to be ∼ 370 Mpc (Wikipedia: Cosmological principle: Violations of homogeneity ). However, there may be structures that are ∼ 1 Gpc in size scale (Wikipedia: Cosmological principle: Violations of homogeneity ), but these may be just extreme fluctuations that may NOT be too important average structure formation (AKA large-scale structure formation).
Taking the scale 370 Mpc a valid, one can infer (from a calculation NOT give here), the radius of a comoving frame should be ∼ 320 Mpc for local observable universe.
However, this radius implies a recession velocity (cosmological growth of outer space rate) for the spherical surface of the comoving frame of ∼ 7.5 % of the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns. Such a high recession velocity means the comoving frame is verging on requiring relativistic physics (combined special relativity (1905) general relativity (1915)) for high accuracy analysis of the INTERNAL motions. However, using relativistic physics means, you are NOT imposing inertial frames. You are allowing inertial frame behavior to emerge from the reality where it will.
However, actual structure formation computer simulations mostly use Newtonian physics and obtain large scale structure that matches the observations quite well so far. Structure formation computer simulations using relativistic physics have been done, but they are vastly more computationally intensive that Newtonian physics ones and have to make simplifying assumptions to make them feasible.
Image 3 Caption: The mean expansion of the universe is illustrated in the upper panel. Recall gravitationally bound systems (and all other bound systems too) do NOT participate in the expansion of the universe at all. The expansion of the universe according to general relativity is the literal growth of space (which is a structure NOT emptiness) between gravitationally bound systems. In Image 3, the the distances between example galaxies and dwarf galaxies all scale up with the mean expansion of the universe (i.e., they scale with cosmic scale factor a(t), where t is cosmic time measured from the Big Bang singularity which was lookback time equal to the age of the universe = 13.799(21) Gyr. Note real astro-bodies participating in the expansion of the universe have superimposed peculiar velocities that add to the recession velocities that give the mean expansion of the universe and so the scaling up of distances is NOT perfect for real astro-bodies.
To return to comoving frames: The average motion of a comoving frame is the general growth of distances between astro-bodies participating in the expansion of the universe. So comoving frames are NOT gravitationally bound systems unlike most celestial frames that are in common use.
The astro-bodies participating in the expansion of the universe are usually galaxy clusters, galaxy groups, and field galaxies (i.e., galaxies NOT in galaxy clusters NOR galaxy groups). Of course, these astro-bodies all have peculiar velocities superimposed on the mean recession velocities of the mean expansion of the universe as discussed with Image 3. Thus, the astro-bodies though participating in the expansion of the universe are NOT participating in the mean expansion of the universe.
Gravitationally bound systems do NOT participate in the expansion of the universe and their motions are analyzed in celestial frames smaller than comoving frames.
What about an actual comoving frame centered us? "Us" being any of the centers of mass, the Solar System, Milky Way, or the Local Group of Galaxies.
Can we determine our motions relative to it?

figure UNDER RECONSTRUCTION BELOW
(see Wikipedia: International Celestial Reference System and its realizations: Realizations) absolute rotation (see International Celestial Reference System and its realizations)
Our Local Comoving Frame:
In fact, we can measure our local motions relative to our local comoving frame to good accuracy/precision by measurement of the cosmic microwave background (CMB).
The CMB is just electromagnetic radiation (EMR) in the microwave band (fiducial range 0.1--100 cm). It strongest in the energy/frequency/wavelength bands ∼ 1--22 cm and has one of the most perfect blackbody spectra found in nature (see Wikipedia: Cosmic microwave background: Features). It is a relic of the Big Bang era speaking loosely. It permeates the observable universe and, according to Big Bang cosmology (which is highly trusted), it is isotropic when viewed in a comoving frame.
In non-comoving frames, the CMB is distorted by a direction-varying Doppler shift due to the motion of that non-comoving frame relative to the local comoving frame. For observers on Earth, this direction-varying Doppler shift is called CMB dipole anisotropy (see Wikipedia: CMB dipole anisotropy (ℓ=1); Caltech: Description of CMB Anisotropies). The CMB dipole anisotropy is further explicated in file cmb_dipole_anisotropy.html.
We will NOT elaborate on the CMB here. But we can give some local velocities determined using it:
The Velocity Field Olympics: Assessing velocity field reconstructions with direct distance tracers: Richard Stiskalek, et al., arXiv, arXiv, 2025, Jan31, 25 pages: Research: On the motions of the local comoving frame out to cosmological redshift z ≅ 0.05 (r ≅ 200 Mpc, t_lookback ≅ 0.3 Gyr).
How are structure formation computer simulations done using comoving frames?
Only an incomplete answer can be given here.
How they are done:
1. First, note that the term comoving frame (which yours truly likes) is probably NOT used by anyone doing those computer simulations. The main reason is that those computer simulations are trying to calculate the average structure formation (AKA large-scale structure formation) of the whole observable universe, NOT of any particular comoving frame. In fact, we only theorize about the average initial conditions of the observable universe and NOT any particular part thereof. Therefore, we can NEVER calculate the current large-scale structure of the local observable universe from early in the cosmic time. We can calculate how it will evolve in the future from cosmic present t_0 = to the age of the observable universe = 13.797(23) Gyr (Planck 2018) using current large-scale structure of the local observable universe as initial conditions and this has been done.
2. The computer simulations start early in the cosmic time at the recombination era (cosmic t = 377,770(3200) y after the Big Bang) with the right amounts of gravitational potential energy and kinetic energy as suggested by observations and small density fluctuations in the then existing matter (i.e., dark matter and primordial cosmic composition (fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7).
  The density fluctuations are determined by a combination of cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009)) and inflation theory.
  The computer simulations is just run forward in cosmic time using Newtonian physics in state of the art structure formation computer simulations.
  In fact, structure formation computer simulations typically use a cube for their computational domain rather than a sphere.
  Yours truly believes they do this to impose periodic boundary conditions in a good way on the computational domain. The periodic boundary conditions allow you to account in a good way for the observable universe outside of the computational domain in a good way.
For the results of structure formation (AKA large-scale structure formation) computer simulations and some related results, see the videos below (local link / general link: large_scale_structure_videos.html) further dynamically illustrate the formation of large-scale structure.
The goodness-for-analysis of relatively isolated celestial frames means you should NOT try to extend their application much beyond their actual size: i.e., beyond the physical extent of the systems of astro-bodies defining them. This is just a practical desideratum.
If you need to analyze motions of astronomical objects outside of the celestial frame you are using, then you should probably use a larger celestial frame in the nested hierarchy of celestial frames that includes those astro-bodies.
If you need to to deal with the observable universe as a whole, then you do NOT use celestial frames at all. You use cosmological model. The most standard of these are Friedmann equation models which are solutions for the Friedmann equation which is derived from general relativity plus simplifying cosmological assumptions.

File: Mechanics file: frame_hierarchy_astro_1bb.html .