Image 1 Caption: A cartoon illustrating the hierarchy of celestial frames (CFs) (called center-of-mass inertial frames in the cartoon) in the observable universe and an astrophysical rotating frame (attached, e.g., to a moon, planet or star). In our discussion below, we do NOT consider rotating frames. For those, see the file frame_rotating.html.

Features:

1. A celestial frame (CF) is an inertial frame attached to the center of mass of a system of objects. Recall inertial frames are free-fall frames unrotating relative to the observable universe (see The Basics of Inertial Frames).

   The internal forces (including the internal gravitational fields) cancel out for the center of mass motion by Newton's 3rd law of motion.

   In fact, as the description suggests, celestial frames are very general and often one just considers special cases.

   Below we only consider one case which is the very importance case of the astrophysical realm.

   A mathematical explication of celestial frames is given at at Celestial Frames (CFs).

2. Note the name celestial frame was just invented by yours truly since a name for celestial frames was needed.

   Note also that yours truly also often uses celestial frame as a synonym for the system defining the celestial frame. It is just natural to do so.

3. The celestial frame case we consider in our discussion is as aforesaid in the astrophysical realm.

   celestial frames in this case consists of astronomical objects that can be treated as point masses. The treatment of astronomical objects as point masses is the subject of celestial mechanics and N-body simulations.

   The simplest case is when the external gravitational field is uniform over the whole celestial frame Then all the internal motions relative to the center of mass (AKA the barycenter) are completely determined by the celestial frame and you do NOT need to refer to the rest of the observable universe as far as motions are concerned. If the astronomical objects in such celestial frame are all gravitationally bound together, then one has a closed system.

4. In most celestial frames, one can do the treatment in the classical limit using Newtonian physics. Sometimes relativistic physics is needed.

5. What is the cause of the external gravitational field? Formally the whole surrounding universe.

   The gravitational field of the cosmologically remote universe CANNOT be formally treated in the classical limit using Newtonian physics.

   Friedmann-equation (FE) models of the universe (which are derived from the Friedmann equation which is derived from general relativity) give the behavior of the universe on average by approximating the mass-energy contents of the universe as a perfect fluid (a zero viscosity fluid) of uniform density in mass-energy.

   The FE models predict the expansion of the universe which is general scaling up of all distances between points in the perfect fluid.

   Each of these points defines a free-fall inertial frame which we call comoving frame.

   Now the observable universe is clumpy: there are planets, stars, star clusters, galaxies, galaxy groups (which are just very poor galaxy clusters in yours truly's opinion and won't be mentioned explicitly hereafter), galaxy clusters, galaxy superclusters, etc. The astronomical objects from galaxies upward in size constitute the large-scale structure.

   It is believed that centers of mass of field galaxies (which are NOT in galaxy clusters), galaxy clusters (all of which are gravitationally bound celestial frames in general) approximately define comoving frames. Only approximately because these systems are subject to gravitational perturbations of relatively nearby large-scale structure. Remote large-scale structure averages away its clumpiness and becomes identical in effect to the remote perfect fluid of the FE models which is why we have confidence in the FE models.

   Circa 2023, the scale between nearby and remote is thought to be of order 370 Mpc (see observable_universe_cosmological_principle.html). This value may need to be revised upward (see, e.g., De Marzo et al. 2021).

   The variations in centers of mass velocity of the large celestial frames (field galaxies, etc.) superimposed on the ideal behavior of comoving frames are called peculiar velocities. They can be calculated in principle and to some degree in practice from the gravitational perturbations.

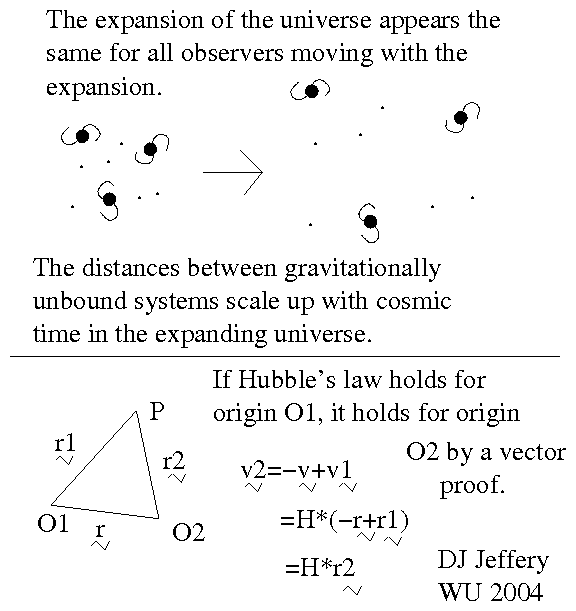
6. Image 2 Caption: The expansion of the universe in the observable universe manifests itself as a scaling up distances between the comoving frames (i.e., the centers of mass of the celestial frames which centers of mass participate in the mean of expansion of the universe). For more on the expansion of the universe, see cosmos_expansion.html.

7. Actually, there is a major qualification to saying the comoving frames are determined by the gravitational field of the universe as a whole.

   The comoving frames are in free fall under that gravitational field, but also an effect that causes the acceleration of the universe. Currently, that effect is hypothesized to dark energy, the simplest form of which is the cosmological constant Λ (pronounced Lambda) which is NOT really an energy form at all. The second simplest form is a constant dark energy which is really an energy form. The two forms act the same in the Friedmann-equation (FE) models, but may be distinguishable in other contexts. It may be that neither of the two forms are the true cause of acceleration of the universe. Hopefully, we will find the true cause someday.

   Because the aforesaid forms act the same in the Friedmann-equation (FE) models, they are, as a shorthand, often just collectively referred to as Lambda since the capital Greek letter Λ (pronounced Lambda) is the symbol for the cosmological constant.

   Lambda (or whatever is causing the acceleration of the universe) is usually unimportant on scales much less than that of the observable universe and is NOT usually mentioned unless it is of importance to an analysis.

8. Returning now to (astrophysical) celestial frames in general, recall that in uniform external gravitational fields all the internal motions relative to the center of mass are determined by the celestial frame itself (i.e., its constituent astronomical objects).

   What if the external gravitational field is NOT uniform?

   Well, you just have to consider effects of the variations in external gravitational field in determining the internal motions.

9. The difference in the external gravitational field at any point from the mass-weighted average external gravitational field is the tidal force (see Celestial Frames (Celestial Frames) for a mathematical treatment). Sometimes the mass-weighted average external gravitational field can be well approximated by external gravitational field at the center of mass of the celestial frame.

   If the tidal forces are extreme, perhaps you should make a different choice of celestial frame to analyze. You might need multiple celestial frames or a much larger one.

   If the tidal forces are sufficiently small, then they can be treated as gravitational perturbations using perturbation theory.

   In between cases take more work.

   Note that the tidal force to lowest order (i.e., in 1st approximation) falls off as 1/r**3, where r is of order the distance between the external gravitational field source and the center of mass of the celestial frame. The 1/r**3 fall is faster than the 1/r**2 fall off for the gravitational field on center of mass of the celestial frame. This implies that the tidal forces in many cases will be rather small gravitational perturbations.

   Note that the tidal forces of remote sources of gravity tend to average to zero. They definitely do so for cosmologically remote scales and usually on much smaller scales for celestial frames smaller than galaxies. In fact, for planetary systems, the tidal forces all the rest of the observable universe are usually completely negligible.

10. In the astrophysical realm there is a whole hierarchy of relatively isolated gravitationally bound celestial frames. Image 1 illustrates the hierarchy in a cartoon. A NOT exhaustive specification of the celestial frames in the hierarchy is:
    1. Planet-moon systems consist of a parent planet and its moons. All the bodies orbit their mutual center of mass which is usually very close to the center of the parent planet, but NOT always inside it. The orbits are usually very regular over short time cosmic scales (i.e., much less than a gigayear (Gyr)). The center of mass of a planet-moon systems orbits the center of mass of its parent planetary system usually in a very regular way over short time cosmic scales.
    2. Planetary systems consist of a parent star or multiple stars for multiple star systems, planet-moon systems, and smaller objects (e.g., asteroids and meteoroids). All the bodies orbit their mutual center of mass which is usually very close to the center of the parent star in NON-multiple star systems, but NOT always inside it. In multiple star systems, the planetary system center of mass may NOT be close to any star or it may be close to a star that overwhelmingly dominates the mass of the planetary system. If the planetary system is NOT in a star cluster, its center of mass directly orbits its parent galaxy center of mass in a chaotic way. The chaos is because of the many chaotic astronomical perturbations the planetary system is subject to. The same remark applies, mutatis mutandis, whenever chaotic orbits are referred to.
    3. Star clusters consist of stars (or overly exactly planetary systems). All the stars orbit the star cluster center of mass in a chaotic way. The star cluster center of mass orbits its parent galaxy center of mass in a chaotic way.
    4. Galaxies consist of stars, star clusters, interstellar medium (ISM), and dark matter (the favored theory of which is an exotic fundamental particle) all of which orbit the galaxy center of mass in a chaotic way. The galaxy center of mass if in a galaxy group or galaxy cluster orbits the galaxy group or galaxy cluster center of mass in a chaotic way. On the other hand, field galaxies (those NOT in galaxy clusters) may approximate comoving frames, but often with strong peculiar velocities.
    5. Galaxy clusters consist of galaxies, intracluster medium, and dark matter. These constituents orbit the galaxy cluster center of mass in a chaotic way. Usually, galaxy cluster centers of mass approximate comoving frames, but often with strong peculiar velocities.
    6. Galaxy superclusters? They are usually rather ill-defined collections of galaxy clusters and field galaxies are NOT usually gravitationally bound systems Because they are ill-defined and unbound, they are usually NOT usefully regarded as celestial frames. Their constituents galaxy clusters and field galaxies are usefully regarded as celestial frames as implied above.

11. Most of the celestial frames in the hierarchy listed above are NOT sufficiently isolated that they can be considered in a uniform external gravitational field, except as a 1st order approximation. The usual exception is planetary systems (counting their stars or multiple stars as part of the celestial frames, of course). Planetary systems are usually so far apart relative to their size (as illustrated in Image 3 below) that they exert NO significant gravitational perturbations on each other.

    

12. Image 3 Caption: An artist's conception of planetary systems spread through space. The separations of the planetary systems are NOT to scale. The ratio of nearest neighbor planetary system distance to planetary system size scale is of order (1 parsec (pc))/astronomical unit (AU)) = 206264.8062 ... . The planetary systems shown are all see nearly edge-on, but, of course, all orientations are possible.

13. Larger structures than planetary systems (e.g., star clusters, spiral arms, the embedding galaxies, galaxies, and always the observable universe) collectively usually provide very uniform external gravitational fields over the size scale of planetary systems.

14. A last point to expand on is the question "what orbits what?"

    Most generally, orbit just means motion determined by the gravitational field, (plus relatively small for non-gravitational astronomical perturbations) relative to a celestial frame.

    However, usually when we say orbit without qualification, we mean a gravitationally bound rotation about a center of mass relative to the observable universe. That answers the question "what orbits what?"

    For example, we say the Moon, orbits the Earth which is understood as being only 1st order correct. More exactly, both Moon and Earth orbit their mutual center of mass which is inside the Earth at ∼ 0.73 Earth equatorial radii (R_eq_⊕ = 6378.1370 km) from the Earth's center (see Wikipedia: Orbit of the Moon). The Earth-Moon system constitute a celestial frame, of course.

    The orbits just considered are sometimes qualified as physical orbits. This just means that they are orbits that follow from Newtonian physics in a celestial frame.

    The opposite case to a physical orbit is a geometrical orbit which is just motion around an arbitrary origin which is NOT a center of mass for the orbiting object. For example, we say the Sun geometrically orbits the Earth relative to the fixed stars in a sidereal year = 365.256363004 days (J2000). This is the way it looks from our observation point, the Earth: i.e., it is an apparent motion. Recall that in astro jargon, "apparent" has the special meaning of "as seen from the Earth". Note the Earth is NOT a center of mass for the Sun's motion.

Images

1. Credit/Permission: © David Jeffery, 2021 / Own work.
   Image link: Itself.
   
2. Credit/Permission: © David Jeffery, 2004 / Own work.
   Image link: Itself.
   
3. Credit/Permission: NASA, before or circa 2017 / Public domain.
   Image link: Itself. The original link NASA: NASA's Kepler Mission Announces a Planet Bonanza, 715 New Worlds is now, alas, a dead link.