De-htmlized text version of this page
apparent magnitude, absolute magnitude, magnitude difference to intensity ratio a conversion table
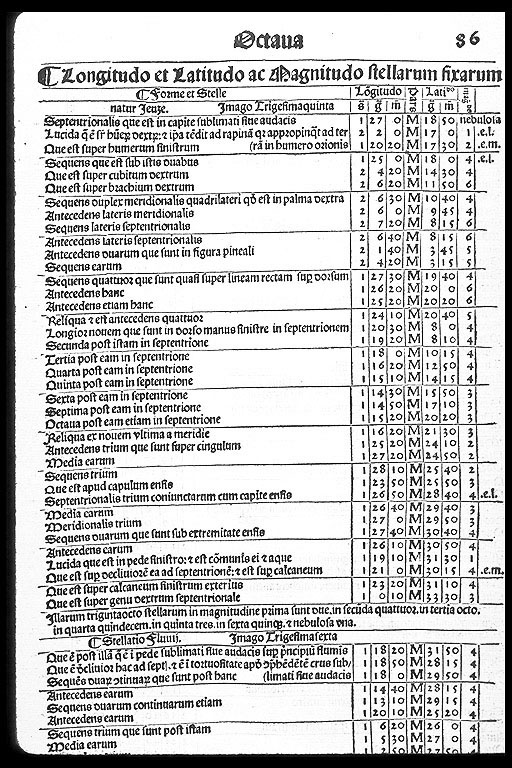
The invention of the MAGNITUDE SYSTEM is often attributed to
HIPPARCHOS
(2nd century BC), but this is only a conjecture. The system
probably did precede
PTOLEMY (circa 100--175)
(To-16).
In any case, Ptolemy effectively established the traditional semi-qualitative
system in the star catalogue of his
ALMAGEST.
He presented the longitudes, latitudes, and magnitudes of 1022 fixed
stars divided into 48 constellations and a handful of nebulae
(No-113;
To-14).
The magnitude system was a description of
STAR BRIGHTNESS IN 6 CLASSES.
1st magnitude described the brightest stars; 2nd magnitude the 2nd brightest,
and so on down to 6th magnitude which described the faintest that could
normally be seen by the
naked eye.
Ptolemy's catalog was certainly based on earlier work, but he probably
made some additions himself.
The magnitude system is only semi-quantitative since measurements were
by the naked eye and assignment of magnitude is based on comparison of stars.
When the TELESCOPE was invented in 1608
(No-328,
Lecture 4.8),
vastly many stars fainter than 6th magnitude were observed and the
magnitude was eventually extended higher values (lower brightnesses).
In the 19TH CENTURY it became possible to measure the INTENSITY OF LIGHT (i.e., energy per unit time per unit area) in different wavelength bands. (In fact in the 19th century the modern concept of ENERGY was first invented and so this ability couldn't have come any earlier.) It was then discovered that the TRADITIONAL MAGNITUDE SCALE corresponded to an approximately LOGARITHMIC measure of intensity. The psycho-physical response of the eye to intensity is, in fact, approximately logarithmic at least under some conditions: i.e.,
Psycho-Physical Eye Response varies under some conditions
approximately as log(I)
where I is energy per unit time per unit area.
Also see the not too informative note on eye
response and
logarithms .
The logical thing to do would be to abandon traditional magnitudes and define a new magnitude scale based on intensity measurements using BASE 10 LOGARITHMS with brighter stars having higher magnitudes. But no that's not what was done.
A 19th century chap named NORMAN R. POGSON---and he's lucky
I think that
his name is merely almost forgotten rather than execrated---in 1856 invented
a new system that retained near consistency with the past.
He (or someone else about then)
noted that 5 traditional magnitudes were about a factor 100 increase
in intensity in what astronomy defines to be the optical wavelength band
of light, and so he (i.e., Pogson) fixed 5 MAGNITUDES as
corresponding exactly to a FACTOR OF 100 INCREASE IN INTENSITY
on his new logarithmic scale and retained that
the smaller magnitude corresponds to the brighter object with an
odious MINUS SIGN.
Note that very bright objects can have NEGATIVE magnitudes.
This is perfectly ridiculous, but that is the convention.
The magnitude difference between object of intensity I_1 and I_2 is
The inverse formula for obtaining intensity ratio from magnitude is
As an aid to CONVERSION from a magnitude difference to an intensity
ratio a CONVERSION TABLE
is provided.
For our course we do NOT need to know a lot about
ABSOLUTE MAGNITUDE.
We just need to know that it measures INTRINSIC BRIGHTNESS of
an object.
Of course, ABSOLUTE MAGNITUDE is backwards too:
BRIGHTER objects have LOWER absolute magnitudes.
Very intrinsically bright objects can have NEGATIVE absolute
magnitudes, of course.
The magnitudes of the brightest stars on the sky is shown
in a
table of
brightest stars.
Sources
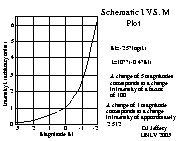His formula for the magnitude M of an object of intensity I is
M=-2.5 * log(I) + CONSTANT ,
where the log function is to BASE 10 and the CONSTANT
which sets the zero-point depends on the particular wavelength band you are
looking at: the zero-point constants are part of the arcana of
astronomy and not just anyone gets told what they are.
M_2-M_1=-2.5 * [log(I_2) - log(I_1)]
=-2.5 *log(I_2/I_1) ,
using the standard logarithm result that the addition/subtraction
of logarithms is the multiplication/division of their arguments.
As constructed
if I_2/I_1=100,
then log(I_2/I_1)=2 , and
M_2 - M_1 = -5 .
So a factor of a 100 increase in intensity causes a decrease in
magnitude by a factor 5.
The brighter object has the lower magnitude.
This WRONG-WAYNESS of the magnitude scale is a constant insult
to RATIONAL CONVENTION in the opinion of yours truly---but no one ever
listens to me.
I_2/I_1 = 10**[-.4(M_2-M_1)]
A difference of 1 magnitude corresponds to an intensity change
by a factor of
10**(-.4)
=2.511886431509580... (which is irrational I suppose)
=2.512 approximately
=2.5 even more approximately .
The 2.511886431509580... number is in fact the base of the astronomical
magnitude logarithmic scale, but we never use that base explicitly:
we always use standard base 10 logarithms with the multiplicative
factor 2.5.
Now the magnitude we measure directly for a star or other astro-body
is called APPARENT MAGNITUDE. Apparent magnitude is based on the
actually intensity we measure on Earth.
Apparent magnitude is what Ptolemy measured and we see.
Apparent magnitude depends on both the luminosity of the star
(energy per unit time in the wavelength band of interest) and
distance through the
inverse-square law of light.
To get a direct measure of LUMINOSITY (the
energy per unit time emitted by a star or other astro body), we define
ABSOLUTE MAGNITUDE.
Absolute magnitude is the apparent magnitude of the astro-body as
measured at 10 parsecs (or about 32.62 lyr)
(Cl-8):
see parsec.