An Outline of Large-Scale Structure Formation

In class, we explicate structure formation using illustrative videos, and so in class we skip far down to feature Structure Formation in Videos.

Features:

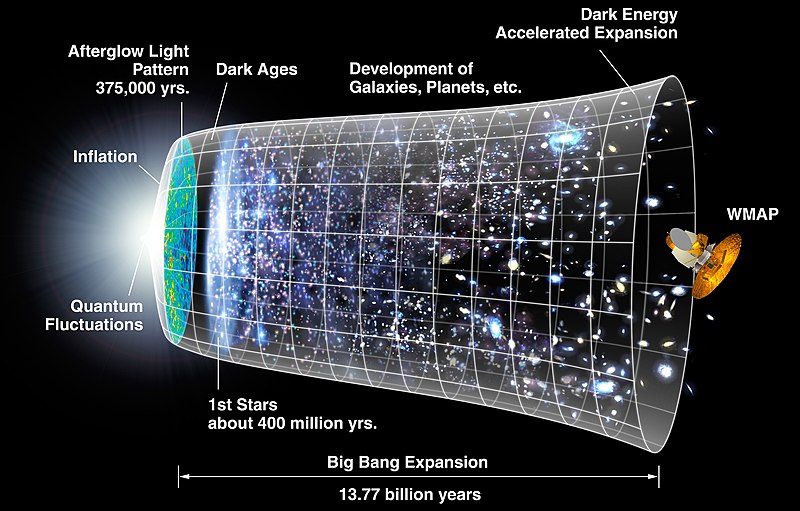
1. Image 1 Caption: A cartoon of the history of the observable universe. Image 1 is given lengthy discussion in Cosmology file: cosmos_history.html.

   Note, the cartoon inlcudes the inflation era (cosmic time ∼ 10**(-36)--10**(-33) or 10**(-32) s from fiducial time zero of standard Friedmann equation models), Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m), and the subsequent evolution of the observable universe according to the Λ-CDM model or some replacement cosmological model (which must be rather close to the Λ-CDM model in most observable effects).

   Note, the initial baryonic matter was created by Big Bang nucleosynthesis (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) and the primordial cosmic composition (which is also almost cosmic present intergalactic medium composition: fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7).

2. The inflation era (cosmic time ∼ 10**(-36)--10**(-33) or 10**(-32) s from fiducial time zero of standard Friedmann equation models)---or whatever happened before Big Bang nucleosynthesis era (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) imposed primordial density fluctuations on the dark matter density distribution which on a large enough scale obeyed cosmological principle: i.e., the assumption that on a large enough scale the observable universe is homogeneous (same in all places) and isotropic (same in all directions). For the cosmological principle, see Cosmology file: cosmological_principle.html.

   The size of the primordial density fluctuations is known by a combination of theory (i.e., inflation) and observation (i.e., the cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009))) (see Wikipedia: Structure formation: Before the first structures).????

3. What happened to the primordial density fluctuations?

   It is a case of the rich getting richer and the poor getting poorer.

   The higher density primordial density fluctuations collapse under their self-gravity to became gravitationally bound systems.

   The lower density primordial density fluctuations to became sitll lower in relative density and the lowest ones evolved to becoming cosmic voids: regions of relative low density.

   Note, the density between gravitationally bound systems was declining in general because of the overall expansion of the universe. The universal expansion is a major background effect opposing the clumping of the matter. It must be considered a given in all our discussions as it is in all calculations of the large-scale structure.

4. Now to 1st order, dark matter and its gravity determine everything since the dark matter is ∼ 85 % of the matter in the observable universe and it interacts with itself and baryonic matter only very weakly if at all, EXCEPT through gravity.

   So the gravitationally bound systems were mostly dark matter and we call these dark matter halos. A whole distribution of sizes of dark matter halos form initially, many of which subsequently merged to make larger dark matter halos.

   Note, we do NOT see dark matter (so far), except through its gravitational effect on baryonic matter which we do see in emitted electromagnetic radiation (EMR).

5. A key point about the dark matter: it was cold dark matter (CDM).

   "Cold" in this context means moving slow relative to the vacuum light speed c = 2.99792458*10**5 km/s ≅ 3*10**5 km/s: i.e., at nonrelativistic velocities relative to the local comoving frames (see frame_hierarchy_astro.html: Comoving Frames).

   Cold dark matter is needed to get the clumping properties needed for the observed large-scale structure.

   Without cold dark matter, the baryonic matter would probably still clump to form stars as we know them, but galaxies and the rest of large-scale structure would look very different from what we see.

   Note, there MAY be exotic hot dark matter (dark matter moving at relativistic velocities) and warm dark matter (at intermediate velocities), but these dark matter forms can only be of secondary importance in structure formation.

   Actually, neutrinos forming the cosmic neutrino background (a relic of the Big Bang from before Big Bang nucleosynthesis (BBN)) were originally a form of hot dark matter, but they lost kinetic energy in a manner similar to that of cosmologically redshifting photons and became a minor contribution to cold dark matter.

6. The baryonic matter to 1st order just follows the dark matter pulled along by the dark matter's gravity.

   Note, baryonic matter is ordinary ordinary matter made of protons, neutrons, and electrons.

   Recall, the initial baryonic matter was created by Big Bang nucleosynthesis (cosmic time ∼ 10--1200 s ≅ 0.17--20 m) and the primordial cosmic composition (which is also almost cosmic present intergalactic medium composition: fiducial values by mass fraction: 0.75 H, 0.25 He-4, 0.001 D, 0.0001 He-3, 10**(-9) Li-7).

   Since then interstellar medium (ISM) has been enriched in metallicity (Z). In the modern/local observable universe is cosmic composition (meaning inside modern galaxies: fiducial values by mass fraction: 0.73 H, 0.25 He-4, ∼ 0.02 metals). The evolution of metallicity (Z) is discussed in Cosmology file: metallicity_evolution.html.

7. Calculations of structure formation (i.e., the formation and evolution of the large-scale structure of the universe) can only be done by computer simulations.

   The 1st order calculations are N-body simulations (which we discuss in features below) which include only dark matter which makes up ∼ 26 % of the mass-energy of the observable universe and ∼ 85 % of the CLUMPABLE mass-energy.

   The dark energy makes up ∼ 74 % of the mass-energy of the observable universe, but it is thought NOT to clump.

8. Because of the dominance of dark matter over baryonic matter, large-scale structure to 1st order can be understood with just dark matter and gravity using N-body simulations which include only particles interacting through gravity alone.

   In fact, in N-body simulations the particles are modeled as point masses which CANNOT hit each other in a body-on-body sense.

   Such N-body simulations in the context of the Λ-CDM model (the current standard cosmological model (c.1995--): Scott 2018) have always done a good 1st order job in reproducing the statistical properties of the observed large-scale structure. Note, the Λ-CDM model fits the observable universe so well overall, that any replacement cosmological model will have to have similar properties to the Λ-CDM model for the calculation of the large-scale structure.

   See N-body simulation videos below in feature Structure Formation in Videos (local link / general link: n_body_videos.html).

   An abbreviated recapitulation of the explication of the present insert (i.e., Cosmology file: large_scale_structure_formation_outline.html) is given in the figure below (local link / general link: large_scale_structure_formation_cube.html).

9. Note, beyond the 1st order, baryonic matter motions and gravity do have a feedback effect on the motions of dark matter.

   So N-body simulations though extremely useful in understanding much structure formation are NOT adequate to to give us the actual existing large-scale structure even for dark matter ALONE.

10. To go beyond a just dark matter universe, one must include baryonic matter and since baryonic matter exerts pressure forces, one must go beyond N-body simulations and use hydrodynamics.

    Note, the pressure forces include ideal gas law pressure, radiation pressure, and magnetic pressure (which if nothing else helps to launch relativistic bipolar jets from central supermassive black hole, and thus provides AGN feedback to structure formation).

    The situation gets worse than just pressure forces.

    Baryonic matter will collapse to form SMALL-SCALE STRUCTURE: stars, galaxies, supernovae (SNe) compact objects (i.e., small white dwarfs neutron stars, stellar mass black holes), supermassive black holes (SMBHs) and active galaxy nuclei (AGNs) (which are powered by supermassive black holes (SMBHs)).

    Dealing with SMALL-SCALE STRUCTURE requires subgrid modeling (e.g., Google: What is subgrid modeling?; Wikipedia: Turbulencesubgrid-scale modeling). Subgrid modeling means that you use approximate prescriptions to deal behaviors smaller than your computational grid. In structure formation, subgrid modeling is now very advanced, but there is an unknown amount of improvement needed to completely adequately account for all large-scale structure.

    Why do we need to deal with SMALL-SCALE STRUCTURE?

    1. SMALL-SCALE STRUCTURE includes most of the observables that we rely on to know about the observable universe (e.g., stars and galaxies) and that we must fit to verify our theoretical understanding of the observable universe.
    2. There is feedback from some of the SMALL-SCALE STRUCTURE (i.e., stellar winds, supernovae, and AGNs) to the large-scale structure including that just made of dark matter.

    An example of calculated result used to compare an observable is the calculated light emitted by the large-scale structure near cosmic noon ∼ 3.8 Gyr (lookback time ∼ 10 Gyr, z ∼ 2) which is illustrated in the figure below (local link / general link: large_scale_structure_cosmic_noon.html).

    ---

11. To pick up the history of structure formation, the early dark matter halos pulled in baryonic matter which clumped into star forming regions which formed the first stars (which were Population III stars) and the first galaxies.

    For formation of the first stars and galaxies is called cosmic dawn (AKA reionization era, z∼6--20, cosmic time ∼ 150 Myr--1 Gyr in the Λ-CDM model).

    The period between recombination era t = 377,770(3200) Jyr = 1.192*10**13 s (z = 1089.80(21)) (where the cosmic microwave background (CMB, T = 2.72548(57) K (Fixsen 2009)) formed an cosmic dawn is called the cosmic dark age (∼ 377 kyr (z ≅ 1100) -- ∼ 150 Myr (z ≅ 20)).

12. We CANNOT here go into details of structure formation through cosmic time, but will give some of the major features below.

13. The basic picture is hierarchical structure formation. In this bottom-up picture, galaxies (starting from initial small galaxies) underwent continuing galaxy mergers resulting in the large range of galaxies of the modern observable universe. The galaxy merger process continues.

    The galaxies themselves became organized in the larger large-scale structure: i.e., the cosmic web consisting of galaxies galaxy groups (⪅ 50 large galaxies), galaxy clusters (⪆ 50 large galaxies), galaxy superclusters, galaxy filaments, galaxy walls, and cosmic voids.

    Galaxies NOT in galaxy groups and galaxy clusters are called field galaxies.

    Note, galaxies, galaxy groups, and galaxy clusters are usually gravitationally bound systems. The other structures listed above are usually NOT gravitationally bound systems.

    Note also, large-scale structure is usually taken to mean the actual existing large-scale structure as opposed to many hypothetical large-scale structures. In the first meaning, large-scale structures is virtually synonym for cosmic web which is just used primarily to emphasize the things (galaxies, etc.) that make up the cosmic web.

14. Image 2 Caption: A map of the large-scale structure of the universe of the local universe out to ∼ 150 Mpc = 0.15 Gpc (∼ 1 % of the observable universe radius = 14.3 Gpc) from the center at the unlabeled Milky Way: i.e., to cosmological redshift z ≅ 0.035 and lookback time ≅ 0.5 Gyr. The map is given a lengthy discussion in Cosmology file: large_scale_structure_z_0x035.html.

15. Among large galaxies (i.e., larger in over all diameter than ∼ 1 Mpc including dark matter halos)??? in the modern/local observable universe:
    1. ∼ 20 % are field galaxies (Wikipedia: field galaxies).
    2. ⪆ 50 % are in galaxy groups (Wikipedia: Galaxy group: Characteristics).
    3. ∼ 30 % are in galaxy clusters.

    The statistics for dwarf galaxies are much less certain and will probably be continually revised for a long time to come.

16. There are many classification galaxy types and most, maybe all, galaxies have multiple galaxy types. For a extensive (but NOT exhaustive) list of galaxy types, see Galaxies file: galaxy_types.html.

    The most basic morphological classification for large galaxies is the Hubble sequence (see Galaxies file: galaxy_hubble_sequence.html). A extension of the Hubble sequence is the de Vaucouleurs system (see Galaxies file: galaxy_vaucouleurs.html).

    Reproducing all the observed galaxy types with the correct statistical distribution is one of the ultimate goals of structure formation computer simulations. Great progress has been made toward this ultimate goal.

17. Note, in calculations of large-scale structure, we are NEVER trying to calculate our observable universe exactly as we see it.

    We are trying to calculate simulated large-scale structure that has the SAME statistical properties as that of the (observed) large-scale structure: e.g., same average number of galaxies of each type per unit volume, same average number of galaxy clusters per unit volume, etc.

    Why CAN'T we calculate our observable universe?

    The exact primordial density fluctuations from Big Bang era in the observable universe CANNOT be completely known. The cosmic microwave background (CMB) T = 2.7260(13) K gives information on the surface of last scattering: i.e., the sphere surrounding us from which the CMB photons that actually reach us last scattered on their radial paths to us.

    For the rest of the locations in the observable universe, we have to assume a distribution of primordial density fluctuations inferred from what the CMB and inflation.

    Of course, a computer simulation of structure formation starts from a particular set of simulated primordial density fluctuations, but that set is just drawn randomly from the assumed distribution of primordial density fluctuations.

    Circa 2025, trhere is NO reason to believe that we will NOT eventually match the statistical properties of the observable universe to high accuracy provided we can the right overall cosmological model.

    Do we have it now. Probably NOT, at least NOT exactly. See the next feature.

18. Since circa 1995, the Λ-CDM model of cosmology has been the standard cosmological model (c.1995--) and the usual basis for structure formation (Scott 2018, p. 10).

    There are some tensions between structure formation computer simulations and observations, but NO falsifications currently.

    Digression on jargon: A falsification is a discrepancy between theory and observation sufficiently large that one judges the theory to be wrong.

    A tension is a discrepancy that does NOT cause one to judge the theory as wrong. The discrepancy may be due uncertainties in the observations or in the application of the theory.

    Tensions suggest there might be a problem with a theory, but more work is needed to show if that is true. More work hopefully will cause the tensions to go away OR turn them into falsifications. Either way, progress.

19. Actually, the Λ-CDM model is suffering a severe tension in regard to the value of Hubble constant (i.e., Hubble tension (direct value ≅ 73 (km/s)/Mpc; Λ-CDM fit value ≅ 67.5 (km/s)/Mpc)) and there are other tensions as well. It seems likely that the Λ-CDM model will have replaced. We take up this story in IAL 30: Cosmology: Limitations and Tensions of our Current Cosmological Theories. See also Cosmology file: big_bang_cosmology_limitations.html.

    However, the Λ-CDM model fits many observations so well that it must approximate any replacement cosmological model very closely. This suggests that structure formation our understanding and calculations will NOT change very much with any replacement cosmological model.

20. EOF

21. Structure Formation in Videos:

    Structure formation (i.e., the formation of the large scale structure of the observable universe) is can be discussed while explicating illustrative videos: first N-body simulation videos, second Large-Scale structure of the universe videos. See also Cosmology file: n_body_videos.html and Cosmology file: large_scale_structure_videos.html.

    EOF

    EOF

Images:

1. Credit/Permission: NASA / WMAP Science Team, before or circa 2006 (uploaded to Wikipedia by User:ArseniureDeGallium, 2006) / Public domain.
   Image link: Wikipedia: File:CMB Timeline75.jpg.
   
2. Credit/Permission: © Richard Powell 2009 (uploaded to Wikipedia by User:Zaerp, 2009) / Creative Commons CC BY-SA 2.5.
   Image link: Wikipedia: File:Nearsc.gif.