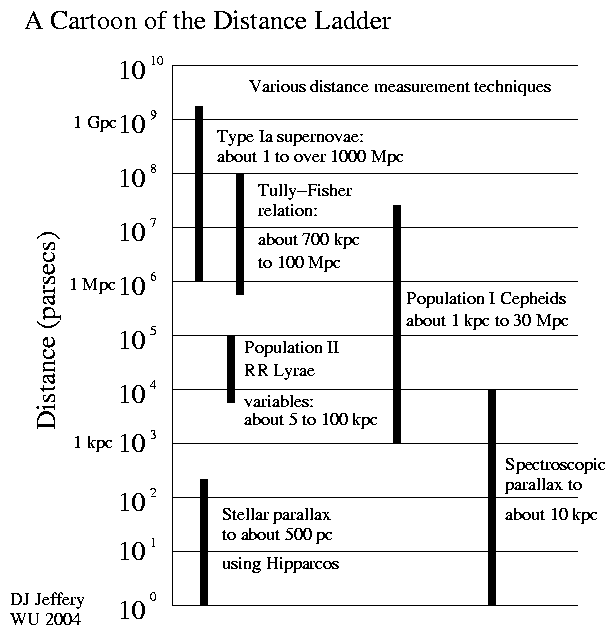
Image 1 Caption: A cartoon of the cosmic distance ladder based on an image in reference FK-587.

The vertical axis is logarithmic distance from the Sun in parsecs: note 1 parsec (pc) = 3.08567758 ... *10**16 m = 206264.806 ... AU = 3.26156377 ... ly ≅ 3.26 ly. The horizontal axis is just to spread out the ranges of applicability of various cosmic distance indicators (distance determination methods) that are used in the cosmic distance ladder.

In this figure/insert, we explicate the cosmic distance ladder.

Features

A cosmic distance indicator is, in fact, a device for measuring cosmic distances. The term cosmic here can mean cosmological or just extraterrestrial.
A cosmic distance indicator is NOT (as usually considered) a direct distance determination method like stellar parallax. It must have a calibration against known calibration standards of known distance (i.e., an empirical calibration) or a theoretical calibration.
At present, the most reliable cosmic distance indicators rely on empirical calibration.
Cosmic distance indicators with only theoretical calibration have NOT usually reached sufficient accuracy/precision to compete in accuracy/precision with those relying on empirical calibration. This might change in the future.
The most basic calibration standards are stars with high accuracy/precision stellar parallax. As discussed in the file general link: gaia_2013_2025.html, the Gaia spacecraft (mission 2013--2025?) circa the 2020s has provided stellar parallaxes and therefore distances of 1 % accuracy out to 10 kpc which is ∼ 1/3 of the diameter of Milky Way galactic disk. These stellar parallax distances are well beyond anything we have had before.
Stellar parallax itself is usually NOT considered a cosmic distance indicator since it does NOT rely on calibration. It is a direct distance determination method.
However, stellar parallax is considered to be the first rung of the cosmic distance ladder which is a series of distance determination methods used to reach greater and greater cosmic distances. To construct the cosmic distance ladder each higher rung usually has to calibrated from lower rung. Of course, the first rung (i.e., stellar parallax) does NOT require empirical calibration.
Yours truly believes that all rungs other than the 1st rung (i.e., stellar parallax) are cosmic distance indicators that must be calibrated, usually empiricially.
Some rungs can be calibrated using stellar parallax distances.
However, other cosmic distance indicators that reach farther in cosmic distance must be calibrated by others that reach less far.
In fact, the cosmic distance ladder is more like a network than ladder with complicated interrelationships between the rungs.
Note each calibration of to reach a given rung adds uncertainty to the overall uncertainty to that calibration of that rung. Hence overall uncertainty usually increases as one goes to larger distance determination. Hopefully, theoretical calibrations will reduce overall uncertainty particularly for distances to remote cosmological astronomical objects.
Image 2 Caption: Approximately the total cosmic distance ladder for scales larger than 1 kiloparsec, except excluding stellar parallax which most consider the 1st rung.
The vertical axis is logarithmic distance from the Sun in multiples of the parsec: note 1 parsec (pc) = 3.08567758 ... *10**16 m = 206264.806 ... AU = 3.26156377 ... ly ≅ 3.26 ly. The horizontal axis is just to spread out the ranges of applicability of various cosmic distance indicators (distance determination methods) that are used in the cosmic distance ladder.

As can be seen, the cosmic distance ladder is more like a network than ladder.
Spectroscopic parallax is usually considered the 2nd rung the cosmic distance ladder. It is NOT shown explicitly, but, in fact, at least two of the rungs have sometimes been calibrated using it: i.e., RR Lyrae variables and Cepheids.
Spectroscopic parallax is explicated in IAL 19: Star Basics I: Luminosity Determination and Spectroscopic Parallax.
In fact, most rungs of the cosmic distance ladder are analogous to spectroscopic parallax where the cosmic distance indicator is a main-sequence star of a given spectral type. Note the name spectroscopic parallax is a misnomer since spectroscopic parallax is NOT a stellar parallax measurement. It uses stellar parallax measurements for calibration.
To explicate, we know to some accuracy/precision luminosity L for some cosmic distance indicator (e.g., a main-sequence star of a given spectral type or Type Ia supernovae (SNe Ia)) and then measure radiant flux (AKA flux) F for some example of this cosmic distance indicator and use the formula
r=sqrt[L/(4πF)]
to determine distance r.
The luminosity L is the "device" requiring calibration. It had to be determined from representative examples of the cosmic distance indicator with known distances r (i.e., calibration standards) and measured fluxes F via the formula
L = (4πr**2)*F .

Of course, there are uncertainties in determining the calibration standard luminosities L from the uncertainties in the determinations of the distances r and the fluxes F.
Note that for sufficiently remote astronomical objects, the astronomical objects have moved significantly during the light travel time for a light signal from them to have reached us (i.e., the lookback time) and that the extinction is negligible or has been corrected for. In these cases, the formulae above do NOT stricly apply and one must do another kind of calculation to get a true physical distance. In the cases when the extinction is negligible or has been corrected for, the distance r calculated from r=sqrt[L/(4πF)] is NOT not a true physical distance, but is referred to as a luminosity distance.
Luminosity distance is one of the direct observables that can go into fitting the free parameters of the Λ-CDM model. For more on luminosity distance, see file cosmos_distance_z_10000.html.
At the top of Image 2 is the Hubble constant H (fiducial value 70 km/s/Mpc) which should actually be replaced in the image by Hubble's law.
Within the Friedmann equation (FE) models (which include all conventional cosmological models), Hubble's law gives all cosmological physical distances (i.e., true physical distances to astronomical objects participating in the mean expansion of the universe or, as it is often expressed, participating in the Hubble flow). Hubble's law is
v = Hr or, inversely, r = v/H ,
where r is cosmological physical distance and v is recession velocity. Alas, neither cosmological physical distance nor recession velocity are direct observables, except asymptotically as cosmological redshift z → 0.
Howsoever, as z → 0, the 1st order or observational Hubble's law applies
zc = Hr or, inversely, r = (c/H)z = L_H*z ,
where vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns, r is cosmological physical distance, and Hubble length L_H = 4.2827 Gpc/h_70 = 13.968 Gly/h_70.
The 1st order Hubble's law has the accuracy as a function of z of order the difference between the curve "naive Hubble" (which is the 1st order Hubble's law) curve "LOS comoving" (which is the cosmological physical distance) in the plots in file cosmos_distance_z_10000.html.
Actually, all cosmological physical distances as a function of cosmological redshift z are given by a cosmological model.
Circa 2020s, the standard model of cosmology (SMC, Λ-CDM model) is the Λ-CDM model.
The Λ-CDM model may need revision or replacement sometime soon (maybe within the 2020s), but even so the cosmological physical distances it predicts are probably accurate to within ∼ 10%.
The main problem with the Λ-CDM model at present is the Hubble tension. Direct measurements give H = 74.03(1.42) (km/s)/Mpc and indirect measurements give H = 67.66(42). The discrepancy is 4.4 standard deviations (i.e., σ's) which is well beyond statistical probability. One or other or both of the measurements are in error, but which is the case. If it is the indirect measurement that is in error, the Λ-CDM model will have to be revised or replaced.
Since the discrepancy between the Hubble constant values 74.03(1.42) (km/s)/Mpc and 67.66(42) is ∼ 10 %, the uncertainty in all distance measurements using the formula r = (c/H)z = L_H*z is ∼ 10 %.
For more on the tensions/problems of the Λ-CDM model, see file big_bang_cosmology_limitations.html.
Note:
1. The Hubble constant is relative rate of the expansion of the universe.
2. Recession velocities are NOT ordinary velocities, but rather are a measure of the rate of growth of space between comoving frames (i.e., inertial frames participating in the mean expansion of the universe).
An incomplete list of cosmic distance ladder indicators (AKA rungs) with names that are often variations of those shown in the images:
For further explication of the cosmic distance ladder, see Cosmic distance ladder videos below.

Images:

Credit/Permission: © User:Brews ohare, 2009 (uploaded to Wikipedia by User:User:File Upload Bot (Magnus Manske), 2012) / Creative Commons CC BY-SA 3.0.
Image link: Wikipedia.

Local file: local link: cosmic_distance_ladder.html.
File: Cosmology file: cosmic_distance_ladder.html.

r=sqrt[L/(4πF)]

L = (4πr**2)*F .

v = Hr or, inversely, r = v/H ,

zc = Hr or, inversely, r = (c/H)z = L_H*z ,