-
We see lots of stars, of course.
- IAL 19 concentrates the most basic features.
- IAL 20 discusses spectral types, and the small scale groupings of stars: multiple star systems, star clusters, stellar associations, stellar populations, and star modeling.
- Almost no direct observations?:
Virtually all observations are, in fact, theory-laden: you need some theory to interpret even the most elementary observations.
So super-pedantically, you could say there are almost NO real direct observations This point is explicated a bit in the figure below (local link / general link: bertrand_russell.html).
- What is a direct observation?:
The fact seems to be that beyond "there is thinking", all other observations are theory-laden: i.e., they depend on theories that we must believe to believe the observations.
But saying there are NO direct observations---except for thinking---is a pretty useless statement in science since it just leads to endless quibbling and qualifications when we want to talk about what we observe, however theory-laden, with an appropriate degree of certainty.
So yours truly---just following a herd---says that a direct observation is one in which all the theories and/or models it depends are regarded as certain to some high standard AND you judge what you observe is in a theory-connecting chain close to you want to observe.
For example, we consider it a direct observation when we measure temperature via an old-fashioned (but never-battery-dead) alcohol thermometer.
But obviously, we are reading volume of an organic compound liquid (usually ethanol), and NOT "temperature".
However, we trust the theory connecting volume and temperature completely and judge the theory-connecting chain to be short.
So we are content with calling the measurement a direct observation.
- What is an indirect observation?:
An indirect observation---just following a herd---is one where some of the theories and/or models it depends are thought to be uncertain to a non-negligible degree OR you judge what you observe is in a theory-connecting chain remote from you want to observe.
For example, most people would call paleoclimate temperatures from ice core isotopic analysis an indirect observation since the theory-connecting chain seems to be long---or maybe they call it a model result since one actually has to use at least a simple model of the Earth's atmosphere to extract paleoclimate temperatures.
Clearly, the difference between direct and indirect observation is vague and rather subjective. Nevertheless, having the two categories is useful in understanding observations and it does NOT seem important that they are NOT precisely specified.
- What is a model result?:
A model result---just following a herd---is information that is obtained by a calculation from a model of a system that has been fitted to the system by many observations.
The result is NOT closely connected to any direct or indirect observation.
The result is believed to the degree that the model is realistic and verified.
Many results in astrophysics are model results.
We put physical ingredients into a model and the model gives us answers. Frequently, there is NO simple explanation for a model result. We say we "understand" the result just by the fact that we understand the ingredients that went into the model.
An example of a model result is the central temperature of the Sun: 15.7*10**6 K (Wikipedia: Sun: Core; Wikipedia: Solar core; Wikipedia: Standard solar model). We have NO direct or indirect measurements of this value. The only direct measurements of the solar core are of solar neutrinos, but they do NOT tell much directly and, in fact, must be understood via the standard solar model (SSM) (Wikipedia: Solar neutrino: Observed data).
- What is the difference between a theory and a model?:
A theory is, among other things, a concise general understanding of some aspect of existence.
A model is similar to a theory, far less general than a theory.
It is often developed just for a particular physical system. For an explication of physical systems, see the figure below (local link / general link: system_environment.html).
Both theories and models typically have free parameters: i.e., controlling variables that must be set by direct or indirect observations.
Other variables for theories and models then follow by a calculation.
For truly grand general theories, the free parameters are fundamental constants: the most grand of these are:
- vacuum light speed c = (2.997 924 58)*10**8 m/s (exact) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns.
- elementary charge e = (1.602 176 634)*10**(-19) C (exact).
- gravitational constant G = (6.674 30(15))*10**(-11) (MKS units) (2024).
- Planck constant h = (6.626 070 15)*10**(-34) J-s (exact) = (4.135 667 696 ...)*10**(-15) eV-s .
- Boltzmann constant k = (1.380 649)*10**(-23) J/K (exact) = (8.617 333 262 ...)*10**(-5) eV/K ≅ 10**(-4) eV/K.
- fine structure constant α = (0.007 297 352 5693(11)) = 1/(137.035 999 084(21)) ≅ 1/137 (2024).
- See Fundamental Physical Constants --- Complete Listing 2018 CODATA adjustment for a list of fundamental constants and the most basic derived constants.
For less grand theories and for models, free parameters come in a wide variety and there are often alternatives sets of free parameters. The chosen set is often just for convenience or for historical reasons.
There is NO hard line between theory and model and the terms are used loosely at times. For example, the Λ-CDM model is a theory in a conventional meaning of the word theory, but it has model in its name by convention. The same is true for the standard model of particle physics: a theory that has model in its name.
- What is a direct observation?:
But what are stars? Their nature? Their physics?
Well, there is a lot to cover actually. Several lectures.
In IAL 19 and IAL 20, we start covering stars with some star basics. The topics are a bit miscellaneous and the order is NOT optimized. Howsoever:
In fact, a full logical presentation of stars would be consist of a step-by-step idealized recapitulation of how the modern understanding of them developed.
But educationally that is unsound. It is just too tedious.
So we will learn to swim in the sea of stars by just jumping into it.
As preview of some of the topics to come in IALs on stars, see the Pleiades open star cluster in the figure below/above (local link / general link: pleiades.html).
First, how do we know about stars?
A quasi-endless cycle of direct observation and modeling improving our understanding continuously.
In other words, the hoary old scientific method. See the figure below (local link / general link: sci_method.html).
To expand a bit on the scientific method
we will discuss a few
methodological points
(on direct observables, indirect observables, model results, and model and theories, etc.)
from the
philosophy of science
relevant to
modeling
stars:
-
Before getting on to stars,
a bit of a digression on the observable universe
is useful.
It is the arena of our current topic stars---and also of galaxies and large scale structure of the observable universe.
The discussion also serves as a preview for galaxies and cosmology that we get to later in:
- Looking Out and Looking Back:
The local observable universe is also the contemporary observable universe since as you look farther out, you look farther back in cosmic time and see the observable universe as it used to be due to the finite travel time of light due to the finite vacuum light speed c = 2.99792458*10**5 km/s (exact by definition) ≅ 3*10**5 km/s ≅ 1 ft/ns.
Now the age of the universe in cosmic time (with zero time at the Big Bang) is currently determined to be 13.797(23) Gyr (Planck 2018) (see Wikipedia: Age of the universe). This very precise value is for Λ-CDM model (AKA concordance model) of cosmology (which fits all known observations pretty well and is our current standard model of the observable universe) and high accurate/precise data Planck 2018.
The LOCAL or CONTEMPORARY observable universe can be loosely defined as being that part of the observable universe at lookback times substantially less than the age of the universe ∼ 13.8 Gyr.
The observable universe and the local observable universe are spheres surrounding us---see the figure below (local link / general link: cosmos_logarithmic_map.html).
- Zooming Out:
Now let's zoom out from us to get a better idea of the local observable universe and the whole observable universe.
- The night sky---which is really close to us:
See the figure below
(local link /
general link: sky_map_winter.html).
- The night sky seen from the outside: See the figure below (local link / general link: milky_way_local.html):
- What we think the Milky Way looks like: See the figure below (local link / general link: milky_way_map.html):
- Our nearest neighbor large galaxy the Andromeda Galaxy (M31): See the figure below (local link / general link: galaxy_andromeda_m31.html):
- The Local Group seen from the outside: See the figure below (local link / general link: local_group.html):
- The nearby galaxy cluster the Virgo Cluster: See the figure below (local link / general link: galaxy_cluster_virgo.html):
- The local large scale structure: See the figure below (local link / general link: large_scale_structure_z_0x035.html):
- The observable universe in cartoons: See the figure below (local link / general link: observable_universe_cartoon.html):
- The night sky seen from the outside: See the figure below (local link / general link: milky_way_local.html):
- Cosmological Redshift:
Recall that in angle, we know where astronomical objects easily---remember equatorial coordinates, right ascension (RA), declination.
But what about in distance?
Actually, NEITHER true physical distance nor lookback time are direct observables, except asymptotically for the nearby observable universe: i.e., relatively nearby galaxies.
The only direct observable cosmological distance measure that can be obtained relatively easily to large physical distance and lookback time is the cosmological redshift
z = (λ_observed-λ_emitted)/λ_emitted ,
where λ_emitted is the emitted wavelength of a source and λ_observed is the wavelength of the source.-
Actually, from the general relativistic cosmology
(more precisely the Friedmann equation models,1917--) we know that
relative expansion of the observable universe since z is
a_observed/a_emitted = z + 1 ,
where the a's are cosmic present = to the age of the observable universe = 13.797(23) Gyr (Planck 2018) and emission values of the cosmic scale factor a(t).So z gives the cosmic scale factor a(t) but NOT cosmic time t since the Big Bang.
It would be wonderful if galaxies had clock faces on them to tell us cosmic time---but they don't.
Because of the expansion of the universe, the wavelength of photons grow as they travel across spacetime: i.e., they redshift. See the figure below (local link / general link: cosmological_redshift_doppler_shift.html).
-
The cosmological redshift arises from
expansion of the universe
and the Local Group does NOT participate
in the expansion of the universe
because it's a
gravitationally bound system.
Also all galaxies have peculiar velocites superimposed on the recession velocity due to the expansion of the universe. These are relatively large for nearby galaxies, but become progressively relatively smaller as one moves farther away from the Local Group.
Fortunately for this nearby region, distance (in all senses) and lookback time are exactly correlated: distance in light-years as a number equals nearly exactly lookback time in years as a number.
- Cosmological Distance Measures:
Looking well beyond the Local Group, we need a cosmological model to go from cosmological redshift z to other cosmological distance measures.
-
A few of the other
cosmological distance measures
can be obtained by direct observation, but NOT easily. These are vital for fitting
cosmological models.
It fits all cosmological observations to within error given the best set of free parameters.
-
However, circa 2021, there
are some tensions with observations, and we may be on the verge of
needing a revised
Λ-CDM model (AKA concordance model)
or a new cosmological model.
For a discussion of the tensions, see
big_bang_cosmology_limitations.html.
Yours truly's discussion of cosmology may need revision soon.
- A Natural Choice for the Defining the Local Observable Universe:
Following from the discussion in the above figure (local link / general link: cosmic_distance_measures.html), one natural choice for defining the local observable universe is the observable universe closer than cosmological redshift z ≅ 0.5 (i.e, which corresponds to lookback time ∼ 5 Gyr and cosmological physical distance ∼ 6 Gly ≅ 2 Gpc).
This choice is a natural one if we make the Sun define the natural units for stars etc. since we know the Sun's age ≅ 4.6 Gyr.
This is NOT the only natural choice.
In fact, one you should probably always specify local observable universe with a cosmological redshift z value for clarity. But most people seem to let context say what their choice is for the meaning of local observable universe.
- Zooming Out:
-
Stars are spheres of hot gas.
- Stars are Hot:
Stars are known to very hot because they are luminous and all matter is a gas at temperatures high enough to make stars as luminous as they are.
Because of their high temperature, we can expect stars to be mainly plasmas.
The surfaces will NOT be completely ionized for cooler stars like the Sun.
Our expectations are, of course, met as the long history of stellar research shows.
- Stars are Spherical:
Self-gravity will pull any sufficiently massive object into a spherical shape---unless it's held up by macroscopic kinetic energy like planetary systems, star clusters, galaxies, galaxy clusters, and accretion disks.
So stars are spheres to first order.
The short explication for why spherical shape for astronomical objects NOT held up by macroscopic kinetic energy:
-
Only the pressure force
can resist sufficiently strong self-gravity,
and the pressure force
CANNOT resist any force that changes shape without compression:
i.e., it CANNOT resist a shear stress.
So there CANNOT be any high hills on an
astronomical objects
of sufficiently strong self-gravity.
Thus, stars,
planets,
moons,
compact remnants
are spherical to 1st order.
A spherical shape is the only one that can resist change in shape due to self-gravity via the pressure force alone.
Qualification: The centrifugal force caused by rotation will cause otherwise spherical astronomical objects to be oblate spheroids: i.e., flattened along the rotational axis. But this is usually a relatively small deviation from spherical shape.
- Stellar Structure:
In IAL 19: Star Basics I, we only consider some introductory aspects of stellar structure. We go into some details of stellar structure and how one calculates stellar structure in IAL 22: The Main Sequence Life of Stars: Stellar Structure and Stellar Modeling.
First off, we note that big hot balls of gas can't be so different in very essential aspects.
The upshot is that in very essential aspects most stars will resemble the Sun in qualitative features even if being very distinct quantitatively.
-
At this point, we have to say that the
compact remnants
white dwarfs
and neutron stars
though called stars
are really distinct from the other things we call
stars.
The are much smaller, much denser, and much less luminous, except that neutron stars can be very luminous in certain wavelength bands. They also have NO nuclear burning unlike (ordinary) stars.
In a very general sense, all stars (that are NOT compact remnants) to be similar. They will have nuclear burning core or nuclear burning layers (if NOT cores), radiative zones, convection zones (nearly always as it turns out), photospheres, magnetic field phenomena, and stellar rotation.
- Stellar Structure Varies:
Now although we expect stars (that are NOT compact remnants) to be a lot alike and like the Sun in a very general sense, in another sense stars must strongly vary since stars vary strongly in properties. For example, in their radiative zones and convection zones: see the figure below (local link / general link: star_convection_2b.html).
The variation of star behavior with stellar mass is explicated in below and in subsequent IALs:
- Stars are Spherical:
- Overall Stellar Composition:
The overall composition of most stars is approximately the primordial solar nebula composition (AKA solar composition) (shown in the figure below (local link / general link: solar_composition.html) except that the metals scale up (a bit) or down by one or more powers of ten depending on the absolute age of the star (e.g., 0.3 Gyr, 1 Gyr, 3 Gyr, 10 Gyr, 13.5 Gyr).
- Surface Stellar Composition:
The composition of the surface of stars is easily known qualitatively from stellar spectroscopy when this can be performed.
Using stellar spectroscopy supplemented by photometry, stellar atmospheres can be modeled to obtain quantitative composition and other parameters, most prominently effective temperature (a sort of average temperature of the photosphere layer).
The surface composition of most stars is very similar to the Sun.
The surface of the Sun is illustrated in the figure below (local link / general link: noao_solar_eclipse_001c.html).
The solar photopshere composition by mass fraction of the best determination as of 2009 is:
hydrogen (H) 73.81 % helium (He) 24.85 % metals 1.34 %
(see Wikipedia: Metallicity: Mass fraction). Recall metals in astro jargon is everything which is NOT hydrogen or helium. The high precision of the above values is given by modeling techniques used to derive them. Yours truly would guess all the values have an uncertainty of order 0.1 at least.The deep interior (i.e., the core) of the Sun and other stars is richer in He because of ongoing nuclear fusion which is discussed in IAL 22: The Main Sequence Life of Stars.
The H and He abundances are approximately accurate throughout the observable universe, except in those minor components: planets, asteroids, interstellar dust, humans, etc.
The abundances of metals vary wildly from about 4 % down to 0.1 % or even much lower, but never 0 as far as we know (HI-414).
The ratios of the metals among themselves often vary much LESS wildly.
-
The metals are all injected into
the interstellar medium
in relatively few processes.
Remember that it is out of the interstellar medium
that astro bodies are formed.
Two important processes supernovae
(giant explosions of old stars) and
strong winds or ejection events from late stages of stars.
The processes tend to produce metals in relatively fixed ratios and the processes tend to occur in relatively fixed ratio and so the cosmic composition of metals tends to have relatively fixed ratios.
Absolute amounts of metals vary more much. As the universe ages, more and more metals are produced.
Therefore, the older a star is lower its metal abundances or metalliticity.
There are some very old stars in the Milky Way that have very low metalliticity.
An example near-record-low-metallicity star is Caffau's star. It has metallicity Z ≤ ∼ 10**(-6). For more explication, see the figure below (local link / general link: star_caffau.html).
- Surface Stellar Composition:
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 19 problems 2--7 on star basics and especially stellar parallax---which students should be able to do based on IAL 2 even before section Distance and Stellar Parallax on stellar parallax.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 19.
-
Now for luminosity,
flux,
and photometry.
- Luminosity:
If we have a star's surface composition, photosphere temperature, and a few other details we won't mention here, we still lack at least one major free parameter for making a simple model.
That free parameter could be any of mass, radius, or luminosity.
None of these are direct observables in general, but luminosity is most accessible.
Luminosity is a star's power output in electromagnetic radiation (EMR): i.e., what its "wattage" is.
There is also luminosity per unit wavelength which is a form of the star's spectrum.
Directly observed spectroscopy and photometry by themselves do NOT give luminosity. One needs more information as we discuss below.
The range of star luminosities is illustrated in the Hertzsprung-Russell (HR) diagram in the figure below (local link / general link: star_hr_named_stars.html).
We will discuss HR diagrams further in IAL 20: Star Basics II.
The Sun's luminosity is
L_☉ = 3.845*10**26 W (Cox-12). L_☉ is often used as a unit itself.For stellar luminosity, L_☉ is a natural unit.The range of stellar luminosity is about 10**(-4) to 10**6 L_☉ (FK-414).
The frequency distribution of stars with luminosity less than the Sun is rather uncertain and it is certainly hard to find up-to-date information on---someone must know, but NOT yours truly.
The frequency distribution of stars with luminosity greater than the Sun decreases rapidly with luminosity (FK-414).
Thus, very luminous stars are relatively rare, but their luminosity tends to make them very conspicuous.
-
Question: What is the
luminosity of
the Sun?
- 60 W.
- 100 W.
- 3.845*10**13 W.
No answers are rightThe luminosity of the Sun is 3.845*10**26 W (Cox-340).
As far away as the Sun is, it is still brighter than a 100 W light bulb seen at ordinary room DISTANCES.
Thus, you ought to know that the biggest number is the only answer that could be right.
Of course, it's NOT right since yours truly is being mischievous.
- Flux:
To measure luminosity and for many other purposes, one needs the concept of flux.
Flux is used in various ways in physics. See the figure below (local link / general link: flux_generic.html) for a general view of flux in physics.
The flux of a light beam is the power per unit area perpendicular to the beam direction integraged over some wavelength band.
Flux per unit wavelength is a spectrum.
One can use flux to mean flux per unit wavelength. As usual context must decide on the right meaning.
Flux is what is observed by us from stars.
Flux is a direct observable.
-
Question: Brightness to the eye or any other
light measuring device increases with light
flux
impinging on the eye or device.
- decreases with DISTANCE from the source.
- does NOT depend on DISTANCE from the source.
- increases with DISTANCE from the source.
The brightness or flux of a source usually:
Answer 1 is right.In subsection Luminosity Determination below, we will go into how flux decreases with DISTANCE from stars.
Brightness doesn't always decrease with distance.
One can have focussed light or converging light beams.
Laser light from an ordinary laser stays tightly beamed although it does spread out slowly, and so has slowly decreasing flux????.
The tight beaming is the reason why laser pointers work.
They depend on the relative spatial positions of the star and the observer.
A star could have any flux or DISTANCE from the Earth.
But to know the INTRINSIC property luminosity, one must know flux and DISTANCE as it turns out.
-
You also have to know the extinction.
But as said in section Introduction, we largely skirt the problem
of correcting for
extinction in
IAL.
- Photometry (Reading Only):
Measuring flux is in principle easy. One just uses standard measuring devices.
But one CANNOT in practice measure total flux integrated (i.e., summed) over all wavelengths for stars because no one device will do that adequately and the Earth's atmosphere is opaque in many wavelength bands as we know from studying the solar spectrum in IAL 7: Spectra.
-
We can get above the
Earth's atmosphere to make measurements
and that is done, of course.
There are limitations on our spacecraft---which as time passes should be reduced.
There is a device that measures total flux---the bolometer. A bolometer absorbs all impinging electromagnetic radiation and converts the electromagnetic radiation energy into heat energy and measures the heat energy change by change in temperature.
Bolometers have many uses, but they are NOT able to measure total flux from astro-bodies.
Extinction also varies with wavelength band. We can't get above the ISM, and so must correct for extinction in wavelength band dependent way.
-
One corrects for the
Earth's atmosphere
and extinction
as best one can.
Here we will just give a bit of a description of how photometry is done.
A broad wavelength band is selected by mounting a passband filter on a telescope that lets through a range of wavelength (the passband) with a varying transmission.
-
The transmission is ineluctable.
One might want 100 % transmission in the passband and 0 % outside, but a practical passband filter will always give 0 % below the passband, then typically a rising transmission that never gets to 100 % followed by a decline back to 0 % at the upper wavelength of the passband.
In the ultraviolet (UV), visible (roughly 0.380--0.750 μm), and infrared (IR), the most standard passbands are UBVRI passbands.
The visible band and the other conventional wavelength bands are illustrated in the figure below (local link / general link: electromagnetic_spectrum.html).
But that can be done usually straightforwardly.
So after a bit of a story, total flux is in principle easy to determine.
But we still need DISTANCE to a star in order to obtain luminosity from flux.
-
The most straightforward way to measure DISTANCE to an
astro-body
is to use parallax
which we briefly discussed in
IAL 2: The Sky.
- Parallax:
Parallax is the shift in angular position of an object as one moves. The animation in the figure below (local link / general link: parallax_animation.html) illustrates parallax dynamically and shows that the remoter the object, the smaller the parallax.
Parallax can also mean a particular angle shift itself.
First, recall that the Greek theta θ is the customary physics symbol for angle. See the figure below (local link / general link: greek_alphabet.html).
Second, recall
There are 360° in a circle. 1 degree = 60 arcminutes = 3600 arcseconds 1 arcminute = 60 arcseconds
- Stellar Parallax:
Stellar parallax is the parallax or shift in angular position of a star on the sky (i.e., relative to astronomical objects so remote that they show NO stellar parallax) as the Earth moves around the Sun.
A second meaning of stellar parallax is the parallax angle for the movement of the Earth over a baseline of exactly 1 astronomical unit (AU) = 1.49597870700*10**11 m (exact).
To understand stellar parallax, we introduce trigonometry---the only bit in this course. The little bit is introduced in the figure below (local link / general link: parallax_trigonometry.html).
Note: baseline small, parallax small as illustrated in the figure below (local link / general link: parallax_small.html).
-
Question: In order to measure
parallax
for a star most easily, one wants to use:
Answer 1 is right.Recall
r(AU) d(parsecs) = ------------- θ(arcseconds)To measure a certain distance d, the angle θ one measures gets bigger (and therefore more easily measured), the bigger the baseline r is.
The largest baseline feasible today is TWICE astronomical unit (AU): one makes measurements half a year apart as the Earth moves us 2 AU in space.
Conventionally, though the fiducial baseline is 1 AU and the stellar parallaxes one measures with this baseline are conventionally called stellar parallaxes.
So the conventional stellar parallax formula with r(AU)=1 is
d(parsecs) = 1/θ(arcseconds) , where the parallax angles are always so small that we never need to worry about using a small angle approximation.-
Question: The stellar parallax formula
is a/an:
- linear relation with θ.
- inverse-linear relation with θ.
- inverse-square relation with θ.
Answer 2 is right.Recall how an inverse-linear relation behaves when plotted. To refresh your memory, see the figure below (local link / general link: function_behaviors_plot.html).
The smaller θ, the larger the distance.
Astro-bodies at very large distances will have immeasurably small parallaxes.
The figure below (local link / general link: parallax_stellar.html) illustrates how distances are determined using stellar parallax.
Determining stellar parallax is NOT quite as simple in practice as the figure suggests.
- Actual Measurements of Stellar Parallax:
Even the closest stars are so far away that they have sub-arcsecond parallax: it required the degree of astronomical accuracy first achieved in the 19th century to measure such small angles.
Historically, the lack of observable stellar parallax was an argument against the moving Earth cosmologies since the time Aristotle (384--322 BCE)????, and thus an argument against heliocentric solar system as Johannes Kepler (1571--1630), for example, well understood. See the unmoving Earth in Aristotelian cosmology in the figure below (local link / general link: aristotle_cosmos.html).
But stars are NOT pasted on a real celestial sphere, and so stellar parallax was eventually measured. See the figure below (local link / general link: friedrich_bessel.html) and Stellar parallax videos below that below (local link / general link: stellar_parallax_videos.html).
- EOF
- Distances Between Stars:
To digress for a moment on distances between stars, we note that inside galaxies the distances to nearest-neighbor stars (NOT in multiple star systems) are typically of order 1 parsec.
-
Note:
- 1 parsec = 3.0856776*10**16 m = 3.2615638 lyr ≅ 3.26 lyr ≅ 3 lyr = 206265 AU (Cox-12).
- 1 solar radius = 6.95508*10**8 m = 0.4652*10**(-02) AU.
- The radii of largest stars ⪅ 10 AU . Note, the largest stars are red hypergiants (which are NOT main-sequence stars). The record largest star as of 2022 is Stephenson 2-18 at ∼ 10 AU in radius.
-
Question: Compared to the interstellar distances,
stars are:
- huge.
- of the same size scale.
- pinpricks.
Answer 3 is right.Note, we are implicitly NOT referring to stars in multiple star systems which can be quite close together: an astronomical unit (AU) = 1.49597870700*10**11 m (exact) or even much less.
The finite size they have to the naked eye and in most images is a result of the Earth's atmosphere, diffraction, and often observing technique.
With special techniques some very large stars can be resolved barely from the GROUND. Those special techniques are still limited to bright objects.
From space, above the fluctuating Earth's atmosphere---which makes stars twinkle---one can resolve a few very close, large stars with the Hubble Space Telescope (HST). For example, Betelgeuse (α ORI): see the figure below (local link / general link: betelgeuse.html).
-
Question: Matter-striking-matter stellar collisions are:
- frequent.
- extremely rare.
Answer 2 is right.In fact, because stars are so minute compared to interstellar distances, even when whole galaxies can collide, it is unlikely that there are any direct star-star collisions (FK-596; CK-398).
- The Present, Past, and Future of Stellar Parallax Measurements:
Ground-based observations have difficulty measuring very small angles accurately because of the fluctuations in the Earth's atmosphere.
Without special techniques measuring angles much smaller than 0.3 arcseconds are very difficult.
Smaller stellar parallaxes, and, thus greater distances, can be obtained from space.
Below is a list of the present and future of space stellar parallax measurement missions. For the past, see Star file: parallax_space_missions_past.
In fact, relative to stellar parallax, we are already living in the future and it is Gaia spacecraft (2013--2025).
Space stellar parallax measurement missions:
- The European Space Agency (ESA) Gaia spacecraft (2013--2025) is the future now and is explicated in the figure below (local link / general link: gaia_2013_2025.html). The Gaia spacecraft (2013--2025) is now deceased, but its data will be the standard for some years post-2025.
- Stellar Parallax:
In fact, parallax is a direct observable (see above subsection What is a direct observation?). This does NOT it is always most accurate and it is only feasible for relatively nearby stars---but they are getting pretty far way nowadays (see below subection The Present, Past, and Future of Stellar Parallax Measurements). What it means is that theories relied on by parallax are super well understood and are, in fact, elementary and the chain of links between actual thing measured and what you what know is short. Systematic errors are better understood than when you have to rely on the intrinsic properties of astro-bodies to make a measurement (see below section Luminosity Determination and Spectroscopic Parallax).
This method is just that of a terrestrial surveyor.
-
Group Activity:
Form groups of 2 or 3---NOT more---and tackle Homework 19 problems 4--10 on star basics and especially stellar parallax.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 19.
-
In this section, we consider luminosity
and spectroscopic parallax.
- Luminosity Determination:
For spherically symmetric light sources (i.e., those that radiate equally in all directions or have isotropic emission), luminosity, distance, and flux are related by an inverse-square law.
The inverse-square law in this case just follows from the conservation of energy principle. See the figure below.
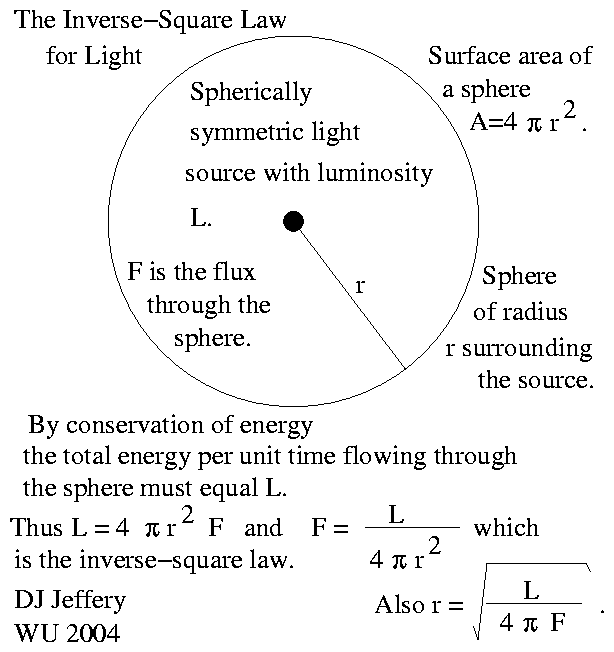
Caption: The inverse-square law for light.
Credit/Permission: © David Jeffery, 2004 / Own work.
Image link: Itself.
The inverse-square law can be used to determine luminosity if one can measure flux F and distance r. The formula is
L = (4πr**2)*F .
For sufficiently nearby stars, one can use stellar parallax to determine distances and then measure flux correcting for Earth's atmosphere and, when possible, for extinction which causes deviations from the inverse-square law.
Using the above formula, one obtains luminosity which is that major free parameter of stellar modeling as we've discussed above in subsection Luminosity.
- Spectroscopic Parallax:
What of stars that are too far away for distance determinations from stellar parallax?
Well, if we have determined the luminosities of nearby main-sequence stars of known spectral types using stellar parallax, then we can invert inverse-square law for luminosity and solve for distances using the known luminosities of the spectral types.
The inverted formula is
r = sqrt[L/(4*π*F)] .
We are assuming the main-sequence stars of a given spectral type all have the same luminosity to within some range. The range becomes an uncertainty in the determination.The main-sequence stars of known spectral types with determined luminosities are, in fact, calibration standards. From the calibration standards, we calibrated main-sequence stars of known spectral types as cosmic distance indicators.
We call the distance determination method using them spectroscopic parallax.
Note, the name spectroscopic parallax is a misnomer since spectroscopic parallax is NOT a stellar parallax measurement. It uses stellar parallax measurements for calibration. However, spectroscopy is done to classify by spectral types remote main-sequence stars. So the "spectroscopic" part of spectroscopic parallax is correct.
Distances from spectroscopic parallax are less accurate than the HIGH QUALITY distances from stellar parallax, but they can extend to farther stars. However, in the age of the Gaia spacecraft (mission 2013--2025?) maybe NOT so much farther. For an explication of the Gaia spacecraft (2013--2025?) and its stellar parallax measurements, see the figure above (local link / general link: gaia_2013_2025.html).
-
The lower accuracy of
spectroscopic parallax
compared to HIGH QUALITY
stellar parallax
is because
spectroscopic parallax distances
depend on:
- stellar parallax distances.
- stellar classification.
- correction for extinction caused by interstellar dust.
These 3 dependencies introduce errors which are propagated to errors in the spectroscopic parallax measurements.
Typically, spectroscopic parallax distances have uncertainties of order 10 % at best (CK-289; FK-430).
- Luminosity Distance:
Spectroscopic parallax distances obtained from the formula
r = sqrt[L/(4*π*F)]
(given above in subsection Spectroscopic Parallax) are a special case of what are called luminosity distances.Luminosity distances can be obtained for any astronomical object (NOT just stars) provided their luminosity is known (i.e., has been calibrated) and extinction is negligible or has been corrected for.
If the astronomical object has NOT moved significantly during the transit time of the light signal from it, one usually just says distance and NOT luminosity distance since the distance is then just a real physical length (i.e., a distance that is measurable at one instant in time).
The term luminosity distance is usually just used when an astronomical object has moved significantly during the transit time of the light signal from it.
In fact, the term luminosity distance is most usually used for cosmologically remote astronomical objects. The universal expansion has moved them significantly during the transit time of the light signal from them.
Cosmological luminosity distances are a direct observable for cosmologically remote astronomical objects of known luminosity and they are predicted by cosmological models. Thus, they are of great interest in determining the true cosmological model and its free parameters.
Luminosity distance is one of the direct observables that can go into fitting the free parameters of the Λ-CDM model (AKA concordance model) which was discussed in the above figure (local link / general link: cosmic_distance_measures.html).
- The First Two Rungs of the Cosmic Distance Ladder:
Stellar parallax and spectroscopic parallax are usually considered as, respectively, the 1st and 2nd rungs of the cosmic distance ladder. For an explication of the cosmic distance ladder, see section The Cosmic Distance Ladder below.
- Examples of Distances, Luminosities, and Other Stellar Quantities:
As examples of various stellar quantities, we can look at the distances, luminosities, and other stellar quantities (star names, Bayer designations, spectral types, luminosity classes, and relative fluxes for brightest stars in Table: Stars of Highest Apparent Brightness below (local link / general link: star_table_brightest_apparent.html).
-
Question: Why are the
nearest stars NOT
necessarily the brightest stars
on the sky
(i.e., stars of highest
apparent brightness)?
- Brightness depends on
luminosity as
well as distance. A dimmer star farther away can be brighter on the sky
than nearby bright star.
- Brightness depends on
luminosity as
well as distance. Luminous stars farther away can be brighter on the sky
than nearby dim stars.
- The nearest stars are
mainly hidden in clouds of
interstellar dust.
Answer 2 is right.Interstellar dust is also a factor since affects the observed brightness or flux of a star, but we won't consider this problem in depth.
- Sirius (the Dog Star) is to the south-east of Orion.
- Betelgeuse is Orion's eastern shoulder
- Aldebaran is the eye of Taurus. One can find it by following a smooth curve from Sirius through Orion's belt and curving northward to Taurus.
- Spectroscopic Parallax:
-
Stellar parallax
and
spectroscopic parallax
are two ways of finding distances beyond the
Solar System.
Spectroscopic parallax can reach to farther distances, because we can determine a star's spectral type to distances beyond where we can determine its stellar parallax.
But spectroscopic parallax depends on stellar parallax to determine the luminosities of the spectral types.
Thus, it is NOT such a basic means of determining distances: it is in fact calibrated using stellar parallax distances.
-
Both stellar parallax
and spectroscopic parallax are
both considered direct observables, but
stellar parallax is MORE
direct.
The distance ladder is a series of methods for determining distances: the methods constitute the RUNGS.
Each RUNG determines farther distances than the next LOWER RUNG, but is usually calibrated by the next LOWER RUNG or other LOWER RUNGS, and thus has lower accuracy than the next LOWER RUNG.
Thus, the farther out we go in the observable universe, the less accurate our distance determinations become.
There are ways of skipping RUNGS, but they have their own uncertainties.
Actually, the distance ladder is more like a network than a ladder with complicated interrelationships between the rungs.
The cosmic distance ladder is explicated in the figure below (local link / general link: cosmic_distance_ladder.html).
Form groups of 2 or 3---NOT more---and tackle
Homework 19
problems 15--20 on the inverse-square law
and the cosmic distance ladder.
Discuss each problem and come to a group answer.
Let's work for 5 or so minutes.
The winners get chocolates.
See Solutions 19.
Group Activity: