


Next: Bra-ket notation
Up: Linear Operators
Previous: Basis functions
In many applications it is convenient to express a physical
amplitude
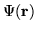 not as an expansion of normalized basis
functions (as in Eq. (
not as an expansion of normalized basis
functions (as in Eq. (![[*]](http://www.physics.unlv.edu/latex2htmlicons//cross_ref_motif.gif) ), but in terms of the following
functions
), but in terms of the following
functions
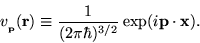 |
(1.18) |
Note that the integral,
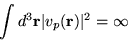 |
(1.19) |
is undefined, and so these functions do not represent
true physical states. Nevertheless they are useful since,
according to Fourier theory, any physical amplitude
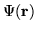 can be expressed in terms of them, i.e.
can be expressed in terms of them, i.e.
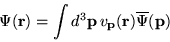 |
(1.20) |
where
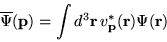 |
(1.21) |
is the Fourier transform of
 .
Now according to definition (
.
Now according to definition (![[*]](http://www.physics.unlv.edu/latex2htmlicons//cross_ref_motif.gif) ),
),
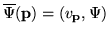 and inserting
into (
and inserting
into (![[*]](http://www.physics.unlv.edu/latex2htmlicons//cross_ref_motif.gif) ) we get
) we get
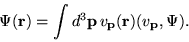 |
(1.22) |
This relation is similar to that given by
Eq. (![[*]](http://www.physics.unlv.edu/latex2htmlicons//cross_ref_motif.gif) ), indeed if we consider
), indeed if we consider
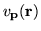 to be a basis function then the above relation is
expansion (
to be a basis function then the above relation is
expansion (![[*]](http://www.physics.unlv.edu/latex2htmlicons//cross_ref_motif.gif) ), except for the replacement of the
discrete index i, and its sum, with that of a continuous index
), except for the replacement of the
discrete index i, and its sum, with that of a continuous index
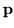 and an integral. (Actually, in this
example, I used three continuous indices,
and an integral. (Actually, in this
example, I used three continuous indices,
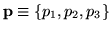 and three integrals
and three integrals
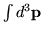 .
Using
the definition of the delta function we find,
.
Using
the definition of the delta function we find,
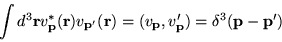 |
(1.23) |
a generalization of the normalization conditions
exhibited by the basis functions ui discussed above. The
functions 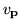 are said to obey delta function
normalization.
are said to obey delta function
normalization.
We can construct a table, analogous to the one given
for the basis functions ui, that is appropriate for the
improper basis functions 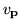 .
pt
.
pt
| improper basis functions, or vectors |
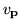 |
| delta function normalization |
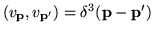 |
| State expansion in basis |
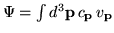 |
| Expansion coefficients |
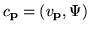 |
| Closure |
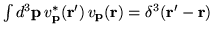 |



Next: Bra-ket notation
Up: Linear Operators
Previous: Basis functions
Bernard Zygelman
1999-09-21
![]() .
pt
.
pt