


Next: Projection operators
Up: Foundations
Previous: Expansion in terms delta
(Read pgs. 109-144)
The Dirac Bra-Ket notation is a concise and convenient
way to describe quantum states. We introduce and define the symbol
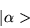 |
(1.24) |
to represent a quantum state. This is called a ket, or a ket vector.
It is an abstract entity, and serves to describe
the "state" of the quantum system. We say that a physical
system is in quantum state 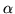 ,
where
,
where 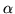 represents
some physical quantity, such as momentum, spin etc, when represented
by the ket
represents
some physical quantity, such as momentum, spin etc, when represented
by the ket
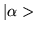 .
.
If we have two distinct quantum states
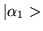 and
and
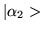 ,
then the following ket
,
then the following ket
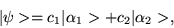 |
(1.25) |
where ci is a complex number, is also a possible state
for the system.
In general, the number of linear independent kets
required to express any other ket, is called the dimension
of the vector space. In quantum mechanics the vector space
of kets is usually non denumerable infinite. We call such a vector
space Hilbert space. We assume that any physical state can be
described by a ket in Hilbert space.
Dirac defined something called a bra vector, designated by
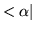 .
This is not a ket, and does not belong in ket space
e.g.
.
This is not a ket, and does not belong in ket space
e.g.
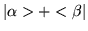 has no meaning. However, we assume
for every ket
has no meaning. However, we assume
for every ket 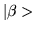 ,
there exists a bra labeled
,
there exists a bra labeled 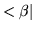 .
The bra
.
The bra 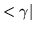 is said to be the dual of the ket
is said to be the dual of the ket
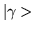 .
We can ask the question: since
.
We can ask the question: since
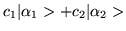 is a ket, what
is the dual (or bra vector) associated with that vector?
is a ket, what
is the dual (or bra vector) associated with that vector?
The answer is,
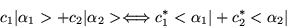 |
(1.26) |
where
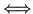 signifies a dual correspondence.
This is an anti-linear relation.
signifies a dual correspondence.
This is an anti-linear relation.
Dirac allowed the the bra's and ket's to line up back to
back, i.e.
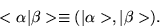 |
(1.27) |
The symbol
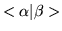 represents a complex
number that is equal to the value of the
inner product of the ket
represents a complex
number that is equal to the value of the
inner product of the ket 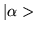 with
with 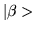 .
We note, according to the above definition, that,
.
We note, according to the above definition, that,
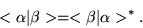 |
(1.28) |
Dirac also defined something called an outer
product,
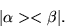 |
(1.29) |
An outer product is allowed to stand next to a ket on its
left, or next to a bra on the bra's right. Lets
define
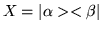 ,
then if
,
then if 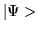 is an arbitrary
ket, one is allowed to construct
is an arbitrary
ket, one is allowed to construct
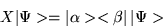 |
(1.30) |
It looks like we have something
like an inner product on the r.h.s of this equation. Indeed,
according to
the associative axiom of multiplication, we are allowed
to put parenthesis around the quantity
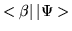 and equate it to the value of the inner product
and equate it to the value of the inner product
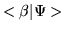 .
Or
.
Or
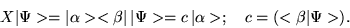 |
(1.31) |
The outer product X is an operator
in Hilbert space. It acts on ket 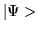 from the left
and turns it into another ket
from the left
and turns it into another ket 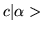 .
Be careful!
for
.
Be careful!
for
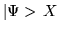 has no meaning, however
has no meaning, however 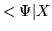 does.
does.
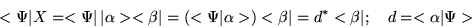 |
(1.32) |
If we take operator A and operate on a ket
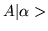 ,
is
,
is
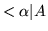 dual to it? In general it is not, however
the dual of
dual to it? In general it is not, however
the dual of
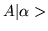 is
is
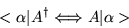 |
(1.33) |
where 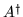 is called the hermitian conjugate
of operator A. Show that the hermitian conjugate
of
is called the hermitian conjugate
of operator A. Show that the hermitian conjugate
of
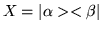 is
is
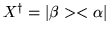 .
.
Sometimes
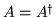 ,
then A is called an hermitian
operator. Hermitian operators play a central role in quantum
theory.
Show that
,
then A is called an hermitian
operator. Hermitian operators play a central role in quantum
theory.
Show that
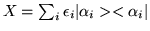 ,
where
,
where
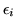 is a real number, is hermitian.
Consider a hermitian operator X, whose eigenstates | a> obey the eigenvalue equation
is a real number, is hermitian.
Consider a hermitian operator X, whose eigenstates | a> obey the eigenvalue equation
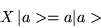 |
(1.34) |
where a is an eigenvalue. Suppose these eigenvalues are
distinct, then set
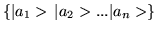 are
mutually orthonormal and form a set of basis kets in
Hilbert space, provided that
are
mutually orthonormal and form a set of basis kets in
Hilbert space, provided that
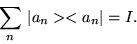 |
(1.35) |
With this set we can express any ket 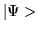 by
by
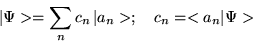 |
(1.36) |



Next: Projection operators
Up: Foundations
Previous: Expansion in terms delta
Bernard Zygelman
1999-09-21
![]() and
and
![]() ,
then the following ket
,
then the following ket
![]() .
This is not a ket, and does not belong in ket space
e.g.
.
This is not a ket, and does not belong in ket space
e.g.
![]() has no meaning. However, we assume
for every ket
has no meaning. However, we assume
for every ket ![]() ,
there exists a bra labeled
,
there exists a bra labeled ![]() .
The bra
.
The bra ![]() is said to be the dual of the ket
is said to be the dual of the ket
![]() .
We can ask the question: since
.
We can ask the question: since
![]() is a ket, what
is the dual (or bra vector) associated with that vector?
is a ket, what
is the dual (or bra vector) associated with that vector?
![]() ,
then A is called an hermitian
operator. Hermitian operators play a central role in quantum
theory.
Show that
,
then A is called an hermitian
operator. Hermitian operators play a central role in quantum
theory.
Show that
![]() ,
where
,
where
![]() is a real number, is hermitian.
Consider a hermitian operator X, whose eigenstates | a> obey the eigenvalue equation
is a real number, is hermitian.
Consider a hermitian operator X, whose eigenstates | a> obey the eigenvalue equation