


Next: About this document ...
Up: Bra-ket notation
Previous: Matrix representation of operators
Suppose we have a basis set
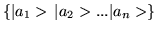 that is complete. These
states might be eigenstates of some hermitian operator, say A.
If we have another hermitian operator B, then the eigenstates
of B could also serve as a complete basis set, lets call it
that is complete. These
states might be eigenstates of some hermitian operator, say A.
If we have another hermitian operator B, then the eigenstates
of B could also serve as a complete basis set, lets call it
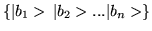 .
We define the
operator
.
We define the
operator
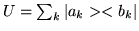 ,
and its adjoint
,
and its adjoint
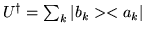 .
Note that
.
Note that
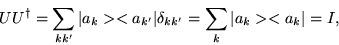 |
(1.46) |
and we can show, in the same manner, that
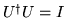 .
In other
words, the adjoint of operator U is its inverse U-1.
Operators that have this property are called unitary operators.
.
In other
words, the adjoint of operator U is its inverse U-1.
Operators that have this property are called unitary operators.
Consider any Hilbert space operator
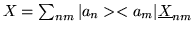 where
where
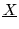 is the matrix
representation of X with respect to basis
is the matrix
representation of X with respect to basis
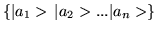 .
Alternatively, we can
express X in terms of the
.
Alternatively, we can
express X in terms of the
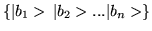 basis.
basis.
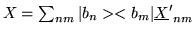 where
where
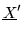 is the matrix representation of X in the
|bn> basis, or
is the matrix representation of X in the
|bn> basis, or
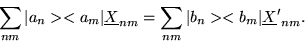 |
(1.47) |
We multiply this relation by the bra <al| on the left,
and by ket |ap> on the right to get
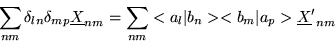 |
(1.48) |
but,
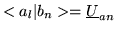 and
and
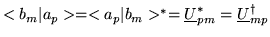 or
or
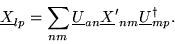 |
(1.49) |
In matrix notation this equation is simply written
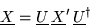 |
(1.50) |
that is, operator X, whose matrix representation is given
by
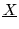 in the |an> basis, is related to
the matrix representation of X in the |bn> basis,
in the |an> basis, is related to
the matrix representation of X in the |bn> basis,
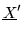 ,
by the above relation. (Note:
,
by the above relation. (Note:
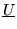 is the matrix representation
of operator X in the |an> representation).
is the matrix representation
of operator X in the |an> representation).
Matrix equations that have this structure
are called similarity transformations, and have important properties.
On of such properties is that the eigenvalues of a matrix are invariant
under a unitary similarity transformation. That means even though
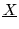 ,
and
,
and
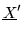 are different matrices,
their eigenvalues are the same since they are related by a unitary
similarity transformation. This implies that we can always find
are different matrices,
their eigenvalues are the same since they are related by a unitary
similarity transformation. This implies that we can always find
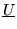 for any operator representation
for any operator representation
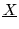 so that the transformed matrix is diagonal. It's eigenvalues are
then distributed on the diagonal.
so that the transformed matrix is diagonal. It's eigenvalues are
then distributed on the diagonal.



Next: About this document ...
Up: Bra-ket notation
Previous: Matrix representation of operators
Bernard Zygelman
1999-09-21
![]() where
where
![]() is the matrix
representation of X with respect to basis
is the matrix
representation of X with respect to basis
![]() .
Alternatively, we can
express X in terms of the
.
Alternatively, we can
express X in terms of the
![]() basis.
basis.
![]() where
where
![]() is the matrix representation of X in the
|bn> basis, or
is the matrix representation of X in the
|bn> basis, or
![]() ,
and
,
and
![]() are different matrices,
their eigenvalues are the same since they are related by a unitary
similarity transformation. This implies that we can always find
are different matrices,
their eigenvalues are the same since they are related by a unitary
similarity transformation. This implies that we can always find
![]() for any operator representation
for any operator representation
![]() so that the transformed matrix is diagonal. It's eigenvalues are
then distributed on the diagonal.
so that the transformed matrix is diagonal. It's eigenvalues are
then distributed on the diagonal.