


Next: Linear Operators
Up: Foundations
Previous: Foundations
Read Pgs. 91-108 in Text.
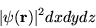 |
(1.1) |
is the probability to find a particle in volume dx dy dz.
We require that
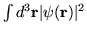 =1.
If
=1.
If
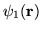 ,
and
,
and
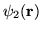 are
possible physical amplitudes,
then so is
are
possible physical amplitudes,
then so is
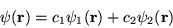 |
(1.2) |
where ci are complex numbers.
We define a scalar, or inner, product
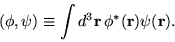 |
(1.3) |
Note
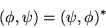 |
(1.4) |
also
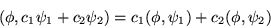 |
(1.5) |
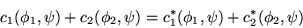 |
(1.6) |
The former is a linear relation, whereas the latter is anti-linear.
If a scalar product vanishes, the pair of functions are said to be orthogonal.
For physical states we require,
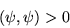 |
(1.7) |
the quantity
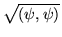 is called the norm of
is called the norm of
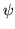 .
The wave functions also obey the Schwarz inequality
.
The wave functions also obey the Schwarz inequality
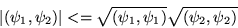 |
(1.8) |



Next: Linear Operators
Up: Foundations
Previous: Foundations
Bernard Zygelman
1999-09-21