


Next: Expansion in terms delta
Up: Linear Operators
Previous: Linear Operators
Consider a denumerable set of possible physical amplitudes, or wave functions, ui,
where i=1,..N and N could be any integer.
If they have the property,
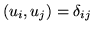 then they are said
to be an orthonormal set. Because of the linear property, we can ask if
it is
possible for any, physical, amplitude
then they are said
to be an orthonormal set. Because of the linear property, we can ask if
it is
possible for any, physical, amplitude 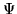 to be expressed as a
linear combination
of the ui basis functions.
We want,
to be expressed as a
linear combination
of the ui basis functions.
We want,
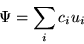 |
(1.14) |
where ci are complex numbers, they are called expansion coefficients.
We take the inner, or scalar, product of this equation with any one member
of the set, lets say uj. Or
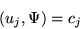 |
(1.15) |
where we have used the orthonormal property of the basis. Inserting
the value of cj back into the previous equation we get,
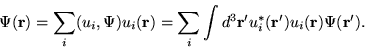 |
(1.16) |
The identity holds if
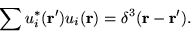 |
(1.17) |
This important relation, if it holds for the set uj, is called the
closure, or completeness, property of the basis functions.
We can summarize the above results in the form of a table
pt
| basis functions, or vectors |
uj |
| Orthonormality relation |
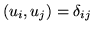 |
| State expansion in basis |
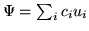 |
| Expansion coefficients |
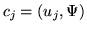 |
| Closure |
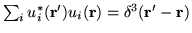 |



Next: Expansion in terms delta
Up: Linear Operators
Previous: Linear Operators
Bernard Zygelman
1999-09-21
![]() then they are said
to be an orthonormal set. Because of the linear property, we can ask if
it is
possible for any, physical, amplitude
then they are said
to be an orthonormal set. Because of the linear property, we can ask if
it is
possible for any, physical, amplitude ![]() to be expressed as a
linear combination
of the ui basis functions.
We want,
to be expressed as a
linear combination
of the ui basis functions.
We want,