3.3 AlSiO

The phase diagram of AlSiO is important for Earth sciences and has attracted great interest. Three known AlSiO polymorphs (kyanite, andalusite, sillimanite) are common minerals in the Earth’s crust and upper mantle. In all these structures, Si atoms are tetrahedrally coordinated, while half of the Al atoms are octahedrally coordinated. The Al octahedra form the -Al-Al- chains, and the remaining Al and Si alternate in neighboring chains (-Si-Al-). The coordination of Al in the -Si-Al- chains is either tetrahedral (sillimanite), fivefold (andalusite), or octahedral (kyanite) ²²⁸. It has to be noted that the prediction of these structures is an extremely challenging test for any global optimization method (These complex structures have low symmetry and relatively large primitive cells with 32 atoms. To illustrate the difficulty of finding the ground state, we generated 10,000 random structures and relaxed them at 10 GPa, and found that none of these structures correspond to the stable phase, kyanite). Energy barriers between these structures are very high and these phases can exist metastably, and even coexist, in nature for millions of years - making direct MD sampling (which covers timescales up to 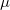s) of these structural transitions clearly impossible. Impressively, an evolutionary metadynamics simulating starting from the low-pressure polymorph, andalusite, has successfully found the other two structures.

Figure 8.4: Enthalpy evolution during the compression on andalusite (AlSiO) at 10 GPa (black line: enthalpies for best structures with constant h; magenta line: enthalpies for best structures after full relaxation).

These simulations were carried out by using a classical potential ²²⁹ and the GULP code. We started the calculation with 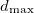=3.0 , 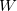=2500 kbar and 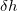=0.4 . Each generation contains 30 structures. Starting from andalusite (32 atoms in the supercell), as shown in Fig. 8.4, in the 8th generation we observed breaking of an interchain Al-O bond in AlO polyhedra, and the structure transformed into sillimanite containing AlO tetrahedra. Sillimanite survived until the 68th generation, when the inter-chain Al-O bonds formed again, increasing coordination of Al from fourfold to sixfold and eventually creating kyanite phase with all Al atoms in the AlO octahedra. The whole picture, as shown in Fig. 8.5, proves that our method was easily able to predict the transitions: andalusite 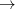sillimanite 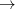kyanite. As a bonus in addition to finding the global minimum structure, the simulation unravels a very non-trivial relationship between the structures (e.g. sillimanite-kyanite) and a crystallographic model of their transformations. For a reconstructive phase transition, one should expect a nucleation-and-growth mechanism, rather than a concerted crystallographic mechanism. However, such a concerted mechanism provides not only a useful simplified view of the real transition, but also input for mean-field theories of phase transformations, and for techniques (such as the Transition Path Sampling(TPS) ²³⁰) that are capable of simulating nucleation and growth phenomena but require a reasonable initial mechanism.

Figure 8.5: Phases observed during compressing andalusite (AlSiO) at 10 GPa. (a) generation 1 (andalusite); (b) generation 4; (c) generation 8; (d) generation 9 (sillimanite); (e) generation 14; (f) generation 63; (g) generation 66; (h) generation 68; (i) generation 69; (j) generation 70 (kyanite).