Crystal Structure Prediction and its Application in Earth and Materials Sciences: Optical Properties

3.2 Optical Properties

Greater density must impact the electronic structure and optical properties. It is well known that DFT underestimates band gaps by $\sim$ 30 %, and therefore we employed both GW and hybrid functionals as implemented in VASP^{215; 216} to accurately estimate band gaps. From the data as shown in Table 7.2, we found that the GW corrected band gap of diamond is 5.4 eV, which is close to the experimental value of 5.5 eV (however, that inclusion of band gap renormalization due to electron-phonon coupling²¹⁷ would worsen the agreement). The electronic band structure of hP3 is shown in Fig. 7.1a. It is a semiconductor with a band gap of 3.0 eV at ambient pressure. The value of the gap would mean intrinsic orange color, but since the band gap is indirect, the material is likely to be colorless. For tI12, the band gap is about 5.5 eV. Finally, electronic band structure of tP12 shows the typical characteristics of insulator. GW gives an indirect band gap of 7.3 eV. tP12 has the largest band gap among all forms of carbon, known of hypothetical. For comparison, the simulated band gaps from GGA, HSE06, B3LYP and GW for different carbon allotropes are also given in Table 7.3.

Table 7.3: Simulated band gaps from different approaches.

Allotropes	GGA	HSE06	B3LYP	GW
diamond	4.2	4.9	5.4	5.2
lonsdaleite	3.8	4.3	4.9	4.7
M-cabon	3.6	4.5	4.8	4.7
bct-4	2.6	3.3	3.9	3.6
chiral	4.1	5.0	5.0	5.2
bc8	2.1	3.7	3.8	3.2
hP3	1.8	2.6	3.1	2.7
tI12	3.7	5.1	5.4	5.1
tP12	5.4	6.0	6.4	7.0

Finally, we investigated dielectric and optical properties of carbon allotropes. We have computed static dielectric constants both in the standard DFT and hybrid functional frameworks. Hybrid functional HSE is believed to give the most reliable results²¹⁶, and for carbon allotropes gives the same level of accuracy as more rigorous GW quasiparticle calculations. Compared to diamond and other allotropes, it is clear that superdense phases have much higher dielectric constants due to their higher density. Refractive index n is important for optical applications, its high value for diamond determines its high brilliance, and it is calculated as ²¹⁸,

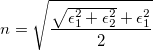$\begin{equation} n=\sqrt {\frac{{\sqrt {\epsilon _1^2 + \epsilon _2^2}} + \epsilon _1^2}{2}} \end{equation}$

(1)

$\includegraphics[scale=0.7]{chapter7/pdf/Fig3.png}$

Figure 7.4: Refractive indices as a function of frequency for the investigated carbon allotropes.

where $\epsilon$ $_1$ and $\epsilon$ $_2$ represent the real and imaginary parts of dielectric function, respectively. Fig. 7.4 shows the frequency dependence of refractive indices of these dense sp $^3$ allotropes in the visible-light frequency range. It can be seen that all the three new superdense allotropes have significantly greater dispersion of light (i.e., the refractive index varies more with frequency) compared with diamond, i.e., if synthesized they will display not only a stronger luster (due to higher refractive index), but also stronger color effects (due to larger light dispersion).