Crystal Structure Prediction and its Application in Earth and Materials Sciences: Crystal Structures

3.1 Crystal Structures

We have performed structure searches at 0 GPa with up to 12 atoms in the unit cell. Our simulations produced the already known structures of diamond, hexagonal diamond (lonsdaleite) and the bc8 structure, but the highest density was indicated for two hitherto unknown structures, which are tI12 (with the tetragonal I-42d symmetry and 12 atoms per unit cell), and hP3 (chiral hexagonal structure with the P6 $_2$ 22 symmetry and 3 atoms per unit cell). The two structures have nearly the same density and at 1 atm are 3.2 % denser than diamond and 2.2 % denser than bc8. Using the chemical analogy approach, we explored the possibility for carbon to adopt the same structure as recently discovered for the new allotrope of germanium (tP12), and this gave us yet another superdense carbon allotrope²⁰⁸.

$\includegraphics[scale=1.0]{chapter7/pdf/Fig1.png}$

Figure 7.1: Crystal structures and band structures of (a)hP3, (b)tI12, (c)tP12 allotropes. The white (dark gray) spheres represent the different types of carbon atoms

$\includegraphics[scale=0.4]{chapter7/pdf/packing.png}$

Figure 7.2: Representaions of various dense carbon allotropes yielded by USPEX, with tetrahedrons being highlighted

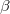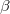Table 7.1 shows the structural data for the three new superdense phases. As shown in Fig. 7.1, all of them have carbon atoms in the tetrahedral coordination (sp $^3$ hybridization). Interestingly, the structural motif of the hP3 phase has a binary counterpart in $\beta$ -quartz SiO $_2$ : in hP3, C atoms occupy the same positions as Si atoms in $\beta$ -quartz. tI12, another superdense polymorph, is related to high pressure SiS $_2$ polymorph with both Si and S atomic positions occupied by C²⁰⁹. DFT calculation shows that tI12 is marginally denser than hP3. 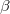We found several $\beta$ -quartz-like dense phases with different ways of packing of tetrahedra as shown in Fig. 7.2. Since these structures share common features in topology, we refer to them as members of the same class of structures, with hP3/ tI12 as the end members. The crystal structure of tP12 is also related to the silicon sublattice in the SiO $_2$ modification keatite. Although diamond has the shortest average C-C bond length among sp $^3$ carbon allotropes, its density is not the highest. For instance, in diamond each carbon atom has 12 second nearest neigbours at 2.52 , while the second nearest coordination sphere of C in hP3 has 14 carbon atoms in the range from 2.27 - 2.60 . This analogy with silica transpires again: quartz (analogy of hP3) and keatite (analogy of tP12) are 13.7 % and 7.7 % denser than cristobalite (diamond form of SiO $_2$ ), respectively, while tridymite (lonsdaleite form of SiO $_2$ ) is 2.6 % less denser than cristobalite²¹⁰.

Table 7.1: Crystallographic data for hP3, tI12 and tP12 structures of carbon at zero pressure

hP3. Space group P6 $_2$ 22. a=b=2.605, c=2.801
Atomic coordinates
C	3c	0.5000	0.0000	0.0000
tI12. Space group I-42d. a=b=2.705, c=8.989
Atomic coordinates
C1	4a	0.0000	0.0000	0.0000
C2	8d	0.8333	0.2500	0.6250
tP12. Space group P4 $_3$ 2 $_1$ 2. a=b=3.790, c=4.661
Atomic coordinates
C1	4a	0.0756	0.0756	0.0000
C2	8d	0.1668	0.3793	0.2171

$\includegraphics[scale=0.7]{chapter7/pdf/Fig2.png}$

Figure 7.3: (a) Enthalpies of various carbon structures relative to diamond. (b) The equations of state of various carbon phases at 0 K.

Are these allotropes totally hypothetical or they can be experimentally obtained? Their energies are high (0.89 - 1.14 eV/atom higher than diamond as shown in Fig. 7.3a), but the same is true for well-known low density allotropes, such as fullerenes (0.44 - 0.72 eV/atom higher than graphite²¹¹) and amorphous carbon (0.70 - 0.99 eV/atom higher than diamond²¹²). Given that much greater density of the hP3, tP12 and tP12 allotropes predicted here, it is possible to obtain them by rapid dynamical compression of low-density forms of carbon. Alternatively, these allotropes can be synthesized by CVD techniques on a suitable substrate. Their dynamical stability (i.e., there are no imaginary phonon frequencies indicates that, once synthesized, these allotropes can exist long at ambient conditions.

Fig. 7.3b shows the equations of state of the hP3, tI12, tP12, bc8, R8, diamond, and several recently reported structures. The hP3 and tI12 allotropes have the most efficient packing of carbon atoms at all pressures up to 400 GPa, and at higher pressures bc8 and R8 will become denser. Remarkably, the computed equations of state indicate that hP3-carbon is even less compressible than diamond; parameters of the third-order Birch-Murnaghan equations of state are given in Table 7.2.

We have also investigated the intrinsic hardness of these three materials using the model²¹³. The predicted hardness for hP3 is 87.6 GPa, which is quite comparable to that of diamond (theoretical hardness 94.3 GPa). Similarly, the theoretical hardnesses of tI12 and tP12 are about 87.2, and 88.3 GPa respectively. The reason why the hardness of hP3, tI12 or tP12 is lower than that of diamond is in the difference of bond strengths. While hP3, tI12 or tP12 have greater bond density than diamond, the bonds themselves are weaker and longer (e.g., the average C-C bond length in hP3 is 1.60 , i.e., significantly longer than 1.54 in diamond).

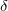Table 7.2: Energy relative to diamond ( $\delta$ E), volume (V), bulk modulus (B $_0$ ) and its pressure derivative (B $_0$ $’$ ), average bond length (d), hardness(H), HSE static dielectric constan $\epsilon$ $_ s$ for the investigated structures. Experimental data are shown in parentheses.

Allotropes	$\delta$ E	V	B $_0$	B $_0$ $’$	d	H	$\epsilon$ $_ s$
	eV/atom	$^3$ /atom	GPa			GPa
diamond	0	5.70	431.1	3.74	1.545	94.3	5.57
²¹⁴	(0)	(5.68)	(446)		(1.54)	(96 $\pm$ 5)	(5.68)
lonsdaleite	0.024	5.71	437.3	3.63	1.548	93.2	5.52
M-cabon	0.159	5.97	392.7	3.88	1.551	89.8	5.52
bct-4	0.196	6.01	411.4	3.50	1.549	91.1	5.42
chiral	0.112	6.22	389.0	3.72	1.555	86.5	5.06
bc8	0.697	5.60	389.6	4.03	1.588	88.8	6.67
hP3	1.113	5.49	432.7	3.71	1.603	87.6	7.73
tI12	1.140	5.48	425.0	3.83	1.603	87.2	7.87
tP12	0.883	5.64	396.0	3.79	1.583	88.3	7.08