| Crystal Structure Prediction and its Application in Earth and Materials Sciences |
Phonon calculations for Mg O
O and MgO
and MgO at pressures of their stability show that no imaginary phonon frequencies exist throughout the Brillouin zone, suggesting that these structures are dynamically stable. Together with our calculated thermodynamic functions, this suggests thermodynamic stability of these compounds. What stabilizes these exotic magnesium oxides at high pressure? To answer this question, we analyzed the electronic structure and chemical bonding for these compounds.
at pressures of their stability show that no imaginary phonon frequencies exist throughout the Brillouin zone, suggesting that these structures are dynamically stable. Together with our calculated thermodynamic functions, this suggests thermodynamic stability of these compounds. What stabilizes these exotic magnesium oxides at high pressure? To answer this question, we analyzed the electronic structure and chemical bonding for these compounds.
Electron Localization Function (ELF) gives information about the bonding character and valence electron configuration of atoms in a compound 165. The ELF pictures show asymmetry of the Mg-O bonds, indicating significantly ionic character of bonding. As shown in Fig. 6.5a, valence electrons in 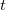 -MgO
-MgO are mainly concentrated around O atoms. Charge transfer was also investigated on the basis of the electron density using Bader analysis 137; 166. In
are mainly concentrated around O atoms. Charge transfer was also investigated on the basis of the electron density using Bader analysis 137; 166. In 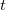 -MgO
-MgO , the net charge on Mg is +1.747
, the net charge on Mg is +1.747  , indicating the nearly complete transfer of valence electrons of Mg to O atoms (just like Mg in MgO: Bader charges are +1.737
, indicating the nearly complete transfer of valence electrons of Mg to O atoms (just like Mg in MgO: Bader charges are +1.737  at 0 GPa and +1.675
at 0 GPa and +1.675  at 600 GPa, respectively). Each O has almost 7 valence electrons (6.873
at 600 GPa, respectively). Each O has almost 7 valence electrons (6.873  ), thus with the formation of singly bonded O-O dumbbell the octet rule is fulfilled. Each O-O dumbbell can be viewed as a peroxide-ion [O-O]
), thus with the formation of singly bonded O-O dumbbell the octet rule is fulfilled. Each O-O dumbbell can be viewed as a peroxide-ion [O-O]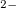 with a closed-shell electronic configuration.
with a closed-shell electronic configuration.
The ELF distribution in 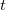 -Mg
-Mg O
O (Fig. 6.5b) also shows strong charge transfer from Mg to O. However, we surprisingly found a very strong interstitial ELF maximum (ELF=0.97) located in the center of Mg-octahedron (Fig. 6.5c). To obtain more insight, we performed Bader analysis. The resulting charges are +1.592
(Fig. 6.5b) also shows strong charge transfer from Mg to O. However, we surprisingly found a very strong interstitial ELF maximum (ELF=0.97) located in the center of Mg-octahedron (Fig. 6.5c). To obtain more insight, we performed Bader analysis. The resulting charges are +1.592  for Mg1, +1.687
for Mg1, +1.687  for Mg2, -1.817
for Mg2, -1.817  for O, and -1.311
for O, and -1.311  for the interstitial electron density maximum. Such a strong interstitial electronic accumulation requires an explanation. The electronic structure (Fig. 6.5e) exhibits intriguingly high occupancy of Mg-
for the interstitial electron density maximum. Such a strong interstitial electronic accumulation requires an explanation. The electronic structure (Fig. 6.5e) exhibits intriguingly high occupancy of Mg-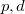 -orbitals with overlapping energy ranges, which implies a strong Mg 3
-orbitals with overlapping energy ranges, which implies a strong Mg 3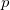 -3
-3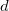 hybridization. At high pressure, strong interstitial electron localization was found in alkali and alkaline-earth elements; for instance, sodium becomes a transparent insulator due to strong core-core orbital overlap 13. As a measure of size of the core region we use the Mg
hybridization. At high pressure, strong interstitial electron localization was found in alkali and alkaline-earth elements; for instance, sodium becomes a transparent insulator due to strong core-core orbital overlap 13. As a measure of size of the core region we use the Mg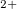 ionic radius (0.72 193), while the size of the valence electronic cloud is represented by the 3s orbital radius (1.28 194). In Mg
ionic radius (0.72 193), while the size of the valence electronic cloud is represented by the 3s orbital radius (1.28 194). In Mg O
O , Mg-Mg contacts at 500 GPa (2.08 A for Mg1-Mg2, 2.37 A for Mg1-Mg1 and 2.43 A for Mg2-Mg2) are only slightly shorter than the sum of valence orbital radii, but longer than the distance at which strong core-valence overlap occurs between neighbouring Mg atoms (0.72 + 1.28 = 2.00 ). Thus, the main reason for strong interstitial electronic localization is the formation of strong multicenter covalent bonds between Mg atoms; the core-valence expulsion (which begins at distances slightly longer than the sum of core and valence radii and increases as the distance decreases) could also play some role for valence electron localization. Strong Mg-Mg covalent bonding is not normally observed; the valence shell of the Mg atom only has a filled 3
, Mg-Mg contacts at 500 GPa (2.08 A for Mg1-Mg2, 2.37 A for Mg1-Mg1 and 2.43 A for Mg2-Mg2) are only slightly shorter than the sum of valence orbital radii, but longer than the distance at which strong core-valence overlap occurs between neighbouring Mg atoms (0.72 + 1.28 = 2.00 ). Thus, the main reason for strong interstitial electronic localization is the formation of strong multicenter covalent bonds between Mg atoms; the core-valence expulsion (which begins at distances slightly longer than the sum of core and valence radii and increases as the distance decreases) could also play some role for valence electron localization. Strong Mg-Mg covalent bonding is not normally observed; the valence shell of the Mg atom only has a filled 3
 orbital, a configuration unfavorable for strong bonding. Under pressure, the electronic structure of the Mg atom changes (
orbital, a configuration unfavorable for strong bonding. Under pressure, the electronic structure of the Mg atom changes (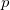 - and
- and 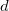 -levels become significantly populated), and strong covalent bonding can appear as a result of
-levels become significantly populated), and strong covalent bonding can appear as a result of 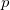 -
-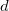 hybridization. There is another way to describe chemical bonding in this unusual compound. We remind that Mg
hybridization. There is another way to describe chemical bonding in this unusual compound. We remind that Mg O
O is anion-deficient compared with MgO; the extra localized electrons in Mg octahedron interstitial play the role of anions, screening Mg atoms from each other. These two descriptions are complementary.
is anion-deficient compared with MgO; the extra localized electrons in Mg octahedron interstitial play the role of anions, screening Mg atoms from each other. These two descriptions are complementary.
We also employed HSE hybrid functional as implemented in the VASP code 195 to estimate band gaps for these compounds; hybrid functionals are known to produce much more accurate band gaps than standard semilocal density functionals. Compared with MgO, which is a wide gap insulator (HSE band gap 9.82 eV at 500 GPa - see Fig. 6.5f), 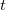 -Mg
-Mg O
O is predicted to have a much narrower band gap of 3.54 eV, while the band gap of
is predicted to have a much narrower band gap of 3.54 eV, while the band gap of 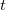 -MgO
-MgO at 500 GPa is 8.11 eV. While MgO remains a wide-gap insulator in a very wide pressure range, the band gap can be decreased by changing the stoichiometry of a magnesium oxide.
at 500 GPa is 8.11 eV. While MgO remains a wide-gap insulator in a very wide pressure range, the band gap can be decreased by changing the stoichiometry of a magnesium oxide.
![\includegraphics[scale=0.5]{chapter6/pdf/fig5-ELF.png}](images/img-0291.png)
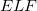 = 0.83) of a)
= 0.83) of a) 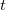 -MgO
-MgO structure; b)
structure; b) 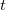 -Mg
-Mg O
O structure at 500 GPa. c) Charge density distribution of
structure at 500 GPa. c) Charge density distribution of 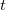 -Mg
-Mg O
O along c axis. Band structure and partial densities of states for d)
along c axis. Band structure and partial densities of states for d) 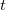 -tetragonal MgO
-tetragonal MgO and e)
and e) 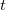 -Mg
-Mg O
O . f) Calculated HSE band gaps as a function of pressure for various Mg-O compounds.
. f) Calculated HSE band gaps as a function of pressure for various Mg-O compounds.