| Crystal Structure Prediction and its Application in Earth and Materials Sciences |
 )
) at high pressure
at high pressureFor the high pressure region, the tetragonal  and trigonal
and trigonal 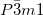 phases are found to be the most stable ones in structure searches at 2-5 GPa and 10-20 GPa, respectively. Interestingly, within the whole pressure range (up to 20 GPa), we did not find the
phases are found to be the most stable ones in structure searches at 2-5 GPa and 10-20 GPa, respectively. Interestingly, within the whole pressure range (up to 20 GPa), we did not find the 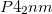 structure proposed by Filinchuk et al. for the
structure proposed by Filinchuk et al. for the 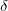 phase 126, but instead found the
phase 126, but instead found the  phase with four formula units (44 atoms) per cell and
phase with four formula units (44 atoms) per cell and  phase with 2 formula units per cell at pressures below 5 GPa (see Fig. 4.2). Given that the
phase with 2 formula units per cell at pressures below 5 GPa (see Fig. 4.2). Given that the 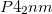 structure is dynamically unstable at ambient pressure, and based on our enthalpy calculations, we hypothesized that the
structure is dynamically unstable at ambient pressure, and based on our enthalpy calculations, we hypothesized that the  and
and  structures might correspond to the experimentally observed
structures might correspond to the experimentally observed 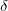 and
and  phases. Further investigation confirmed this suggestion, as we will show below.
phases. Further investigation confirmed this suggestion, as we will show below.
![\includegraphics[scale=1.0]{chapter4/pdf/Fig2.png}](images/img-0230.png)
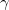 phase) of various structures of Mg(BH
phase) of various structures of Mg(BH )
) as a function of pressure. Enthalpies are given per formula unit. The inset shows the energy per formula unit of
as a function of pressure. Enthalpies are given per formula unit. The inset shows the energy per formula unit of  ,
, 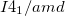 , and
, and  structures including vdW interactions at zero pressure relative to the
structures including vdW interactions at zero pressure relative to the 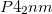 structure.
structure.Lattice constants of the most interesting candidate structures are listed in Table I. The calculated zero-pressure lattice constant ( =
= 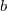 =
=  = 15.79 ) of the
= 15.79 ) of the 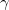 phase is in excellent agreement with the experimental value (15.76 ) 126, which gives a benchmark of the typical accuracy to expect of DFT simulations for this system. For the
phase is in excellent agreement with the experimental value (15.76 ) 126, which gives a benchmark of the typical accuracy to expect of DFT simulations for this system. For the  structure, the Mg atom occupies the crystallographic
structure, the Mg atom occupies the crystallographic 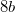 site at (0.5, 0, 0), the B atom occupies the
site at (0.5, 0, 0), the B atom occupies the 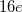 site at (0.533, 0.25, 0.375), and the H atoms are at the
site at (0.533, 0.25, 0.375), and the H atoms are at the 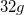 sites with coordinates (0.439, 0.247, 0.295) and (0.627, 0.123, 0.369). For the
sites with coordinates (0.439, 0.247, 0.295) and (0.627, 0.123, 0.369). For the  structure, the Mg atoms occupies the
structure, the Mg atoms occupies the 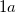 site at (0, 0, 0) and
site at (0, 0, 0) and 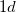 site at (0.5, 0.5, 0.5), the B atom occupies at the
site at (0.5, 0.5, 0.5), the B atom occupies at the 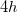 site at (0.25, 0.25, 0.25), and the H atoms are at the
site at (0.25, 0.25, 0.25), and the H atoms are at the 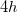 sites with coordinates (0.459, 0.282, 0.210), (0.139, 0.327, 0.089), (0.223, 0.038, 0.286), and (0.174, 0.354, 0.416). From Table I, one can see that relaxing the experimental
sites with coordinates (0.459, 0.282, 0.210), (0.139, 0.327, 0.089), (0.223, 0.038, 0.286), and (0.174, 0.354, 0.416). From Table I, one can see that relaxing the experimental 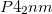 structure, one gets unexpectedly large changes in the lattice constants – so large that, in fact, the relaxed lattice constants of the
structure, one gets unexpectedly large changes in the lattice constants – so large that, in fact, the relaxed lattice constants of the  structure are the closest match to the experimental ones 126. One has to keep in mind that what is called the “experimental" cell parameters in many cases is a non-unique result of indexing powder XRD spectra, and this is the case here.
structure are the closest match to the experimental ones 126. One has to keep in mind that what is called the “experimental" cell parameters in many cases is a non-unique result of indexing powder XRD spectra, and this is the case here.
![\includegraphics[scale=1.0]{chapter4/pdf/Fig3.png}](images/img-0240.png)
 ,
,  , and
, and 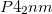 structures of Mg(BH
structures of Mg(BH )
) with the X-ray wavelength of 0.770518 at ambient pressure (a) and 0.36814 at 10 GPa (b) in comparison with the corresponding experimental results (Ref. [123] and Ref. [125]).
with the X-ray wavelength of 0.770518 at ambient pressure (a) and 0.36814 at 10 GPa (b) in comparison with the corresponding experimental results (Ref. [123] and Ref. [125]).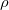 ), bulk modulus (B
), bulk modulus (B ) and its pressure derivative (
) and its pressure derivative (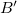 ), and the total energy of the polymorphs of Mg(BH
), and the total energy of the polymorphs of Mg(BH )
) . The energy difference (
. The energy difference (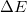 ) including vdW interactions (
) including vdW interactions (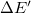 ) is relative to the
) is relative to the  structure.
structure.Symmetry |
|
|
|
|
|
(Theory) |
(Expt) |
||||
|
7.69 |
8.32 |
5.58 |
5.79 |
5.44 |
|
7.69 |
8.32 |
5.58 |
5.79 |
5.44 |
|
12.30 |
10.52 |
5.99 |
5.73 |
6.15 |
|
0.986 |
0.984 |
0.963 |
0.933 |
0.987 |
B |
24.0 |
31.0 |
31.7 |
28.5 |
28.5 |
|
4.3 |
3.6 |
3.6 |
3.6 |
5.8 |
|
-17.0 |
-15.5 |
-13.6 |
0 |
|
|
-21.2 |
-19.3 |
-15.4 |
0 |
 Mg(BH
Mg(BH )
) becomes more stable than the
becomes more stable than the  phase at pressures above 0.7 GPa (Fig. 4.3). In the room-temperature experiment, a pressure-induced structural transformation is observed for the porous
phase at pressures above 0.7 GPa (Fig. 4.3). In the room-temperature experiment, a pressure-induced structural transformation is observed for the porous  phase, and occurs in two steps: The
phase, and occurs in two steps: The  phase turns into a diffraction-amorphous phase at 0.4-0.9 GPa, and then at approximately 2.1 GPa into the
phase turns into a diffraction-amorphous phase at 0.4-0.9 GPa, and then at approximately 2.1 GPa into the  phase 126. The calculated phase transition pressure from the
phase 126. The calculated phase transition pressure from the 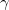 phase to the proposed
phase to the proposed 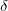 phase with
phase with 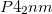 symmetry is 1.2 GPa (the corresponding phase transition pressure for
symmetry is 1.2 GPa (the corresponding phase transition pressure for  phase is 0.8 GPa), which are in good agreement with the experimental values (0.4-0.9 GPa). We note a tiny enthalpy difference between
phase is 0.8 GPa), which are in good agreement with the experimental values (0.4-0.9 GPa). We note a tiny enthalpy difference between  and
and  structures at pressures around 1 GPa. As pressure increases to 9.8 GPa, the
structures at pressures around 1 GPa. As pressure increases to 9.8 GPa, the 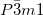 structure becomes the most stable one, in agreement with earlier predictions 128; 136. Bil et al. 131 indicated that it is important to treat long-range dispersion interactions to get the ground state structures of magnesium borohydrides correctly. We have examined the energetic stability of the considered structures through a semi-empirical Grimme correction to DFT energies, stresses and forces 67 (see the inset of Fig. 4.3). When this correction is included, the
structure becomes the most stable one, in agreement with earlier predictions 128; 136. Bil et al. 131 indicated that it is important to treat long-range dispersion interactions to get the ground state structures of magnesium borohydrides correctly. We have examined the energetic stability of the considered structures through a semi-empirical Grimme correction to DFT energies, stresses and forces 67 (see the inset of Fig. 4.3). When this correction is included, the  and
and  structures once again come out as more stable than the
structures once again come out as more stable than the 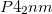 structure, by 21.2 kJ/mol and 15.4 kJ/mol, respectively. Energetic stability seems to correlate with the degree of disparity of bond lengths and atomic Bader charges. The
structure, by 21.2 kJ/mol and 15.4 kJ/mol, respectively. Energetic stability seems to correlate with the degree of disparity of bond lengths and atomic Bader charges. The 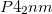 structure has two inequivalent Mg-H distances, 2.26 and 2.07 , compared to 2.11 and 2.07 in the
structure has two inequivalent Mg-H distances, 2.26 and 2.07 , compared to 2.11 and 2.07 in the  structure, and 2.12 and 2.06 in the
structure, and 2.12 and 2.06 in the  structure. As we can see, the more homogeneous bond lengths, the greater stability. Bader charges show the same picture: for H atoms, we find them to be -0.63 and -0.59
structure. As we can see, the more homogeneous bond lengths, the greater stability. Bader charges show the same picture: for H atoms, we find them to be -0.63 and -0.59  in the
in the 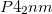 structure, -0.63 and 0.62
structure, -0.63 and 0.62  in the
in the  structure, and -0.63 and -0.61
structure, and -0.63 and -0.61  in the
in the  structure 137. More homogeneous Bader charges and bond lengths in the
structure 137. More homogeneous Bader charges and bond lengths in the  and
and  structures correlate with their greater thermodynamic stability at ambient pressure, in agreement with proposed correlations between local bonding configurations and energetic stability 135.
structures correlate with their greater thermodynamic stability at ambient pressure, in agreement with proposed correlations between local bonding configurations and energetic stability 135.
Our calculations suggest that the 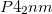 structure, proposed by experiment for the
structure, proposed by experiment for the 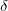 phase, is unstable. This implies that either density functional theory calculations are inaccurate for this system, or experimental structure determination was incorrect. To assess these possibilities, we simulated the XRD patterns of the
phase, is unstable. This implies that either density functional theory calculations are inaccurate for this system, or experimental structure determination was incorrect. To assess these possibilities, we simulated the XRD patterns of the  and
and  structures, and compared them with the experimental XRD pattern of the
structures, and compared them with the experimental XRD pattern of the 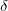 phase at ambient pressure (see Fig. 4.4a). One observes excellent agreement, both for the positions and the intensities of the peaks (including both strong and weak peaks), of the
phase at ambient pressure (see Fig. 4.4a). One observes excellent agreement, both for the positions and the intensities of the peaks (including both strong and weak peaks), of the  structure with experiment 126. The situation is very peculiar: two structures,
structure with experiment 126. The situation is very peculiar: two structures,  and
and 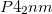 , have nearly identical XRD patterns, both compatible with the experiment – but one,
, have nearly identical XRD patterns, both compatible with the experiment – but one,  , is the true thermodynamic ground state (global minimum of the enthalpy), whereas the other,
, is the true thermodynamic ground state (global minimum of the enthalpy), whereas the other, 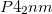 , is not even a local minimum of the enthalpy (dynamically unstable structure, incapable of sustaining its own phonons). In this situation, the true structure is clearly
, is not even a local minimum of the enthalpy (dynamically unstable structure, incapable of sustaining its own phonons). In this situation, the true structure is clearly  . This example gives a clear real-life example of the fact that very different structures can have very similar powder XRD patterns, making structure determination from powder data dangerous, and in such cases input from theory is invaluable. The
. This example gives a clear real-life example of the fact that very different structures can have very similar powder XRD patterns, making structure determination from powder data dangerous, and in such cases input from theory is invaluable. The  structure also has a rather similar XRD pattern, but the peak positions are slightly shifted. Comparison with an independent experimental XRD pattern collected at 10 GPa (Fig. 4.4b) shows that the peak positions and intensities of the
structure also has a rather similar XRD pattern, but the peak positions are slightly shifted. Comparison with an independent experimental XRD pattern collected at 10 GPa (Fig. 4.4b) shows that the peak positions and intensities of the  structure are once again in excellent agreement with the experimental data 128, while the strong peaks of the
structure are once again in excellent agreement with the experimental data 128, while the strong peaks of the  structure at
structure at 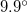 ,
, 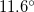 , and
, and 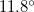 obviously deviate from the observed ones. This reinforces our conclusion that the
obviously deviate from the observed ones. This reinforces our conclusion that the  structure is the best candidate for the high pressure
structure is the best candidate for the high pressure 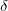 phase. At pressures below 10 GPa a mixture of
phase. At pressures below 10 GPa a mixture of  and
and  phases is possible, as the XRD peaks of these two structures are quite similar. We remind that in the experiment, the
phases is possible, as the XRD peaks of these two structures are quite similar. We remind that in the experiment, the 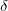 and
and  phases are nearly indistinguishable 126.
phases are nearly indistinguishable 126.
![\includegraphics[scale=1.0]{chapter4/pdf/Fig4.png}](images/img-0250.png)
 phase and (b) the
phase and (b) the  phase at ambient pressure.
phase at ambient pressure.Filinchuk et al. demonstrated the bulk modulus of the 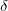 phase (28.5 GPa) is almost three times higher than that (10.2 GPa) reported by George et al. by fitting the Murnaghan equation of state 126; 128. Our third-order Birch-Murnaghan 138 fits of the equation of state yielded bulk moduli of the
phase (28.5 GPa) is almost three times higher than that (10.2 GPa) reported by George et al. by fitting the Murnaghan equation of state 126; 128. Our third-order Birch-Murnaghan 138 fits of the equation of state yielded bulk moduli of the  and
and  structures equal to 24 GPa and 31.7 GPa, respectively, consistent with the measured value (28.5 GPa) 126. The observed large density difference with respect to the
structures equal to 24 GPa and 31.7 GPa, respectively, consistent with the measured value (28.5 GPa) 126. The observed large density difference with respect to the 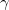 phase at ambient conditions (44%) is equally consistent with 45% (43%) for
phase at ambient conditions (44%) is equally consistent with 45% (43%) for  (
( ) structures 126. Therefore, it is difficult to discriminate between the
) structures 126. Therefore, it is difficult to discriminate between the  and
and  structures by their compression behavior, density or bulk modulus. Our calculations show that the
structures by their compression behavior, density or bulk modulus. Our calculations show that the  structure does not only match all experimental observations for the
structure does not only match all experimental observations for the 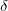 phase and has the lowest enthalpy among all sampled structures at the relevant pressure range, but is also dynamically stable – phonons were computed at 0, 5 and 10 GPa. The phonon densities of states (PDOS) of
phase and has the lowest enthalpy among all sampled structures at the relevant pressure range, but is also dynamically stable – phonons were computed at 0, 5 and 10 GPa. The phonon densities of states (PDOS) of  and
and  phases at ambient pressure are shown in Fig. 4.5, and once again we see a great degree of similarity. The similarity of all characteristics of these two phases parallels the observed similarity of characteristics of the
phases at ambient pressure are shown in Fig. 4.5, and once again we see a great degree of similarity. The similarity of all characteristics of these two phases parallels the observed similarity of characteristics of the 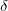 and
and  phases and invites one to propose that while the I41/acd structure corresponds to the
phases and invites one to propose that while the I41/acd structure corresponds to the 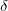 phase, the
phase, the  phase may have the
phase may have the  structure.
structure.