Crystal Structure Prediction and its Application in Earth and Materials Sciences: Empirical potentials

2.1 Empirical potentials

Here one assumes a functional form and then fit the parameters to reproduce a set of data from experiment or high accuracy quantum calculations. The choice of the inter-atomic potential depends on the area of proposed application. There are no purely good potentials, but only potentials that are appropriate for a given problem. The total energy of the system of N atoms with interaction described by an empirical potential can be expanded in a many-body expansion:

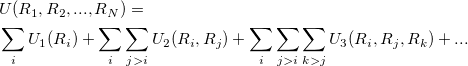$\begin{equation} \label{manybody} \begin{split} & U(R_1,R_2,...,R_ N) = \\ & \sum _ i U_1(R_ i) + \sum _ i \sum _{j>i} U_2(R_ i, R_ j) + \sum _ i \sum _{j>i} \sum _{k>j} U_3(R_ i,R_ j,R_ k) + ... \end{split} \end{equation}$

(9)

where 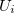$U_ i$ is i-body term. 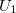$U_1$ is due to an external field or boundary conditions, 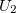$U_2$ is also called pair potential, representing the interaction of any atomic pair.

When this expansion is truncated at 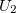$U_2$ , pair potential is used to assume the interaction is only the dependence of up to two-body terms. Pair potentials are very common in physics. Examples of pair potentials include the Coulomb’s law, Lennard-Jones potential, Morse potential and Buckingham potentials.

Lennard-Jones potential

Lenard Jones potential can be expressed as:

$\begin{equation} \label{eq:hard_ lj} U(r_{ij})=4\epsilon [(\frac{\sigma }{r_{ij}})^{12} - (\frac{\sigma }{r_{ij}})^{6}] \end{equation}$

(12)

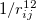where $\epsilon$ is the depth of the potential well, $\sigma$ is the finite distance at which the inter-particle potential is zero. The term $1/r_{ij}^{12}$ is the repulsion between atoms when they get close to each other. Its physical origin is related to the Pauli principle: when the electronic clouds surrounding the atoms start to overlap, the energy of the system increases abruptly. The term 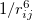$1/r_{ij}^6$ becomes dominant when 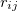$r_{ij}$ increases, representing the attraction due to weak interactions (like bonding in closed-shell systems). Therefore, it could well describe the van der Waals (vdW) interaction in inert gases and molecular systems.

Morse potential

Morse potential is similar to Lennard-Jones but more suitable for the description of a covalent chemical bond.

$\begin{equation} \label{Morse} U(r_{ij})=\epsilon [e^{-2\alpha (r_{ij}-r_{0})} - 2e^{-\alpha (r_{ij}-r_{0})}] \end{equation}$

(13)

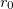$\epsilon$ is the well depth, $\alpha$ controls the width of the potential, and $r_0$ is the equilibrium bond distance.

Buckingham potential

Buckingham potential is a modification of the Lennard-Jones function. The repulsion term of 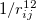$1/r_{ij}^{12}$ in Lennard Jone was chosen by experience. In fact, exponential term gives better description of strong repulsion due to overlap of the closed shell electron clouds, as it is more physical,

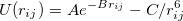$\begin{equation} \label{buckingham} U(r_{ij}) = Ae^{-Br_{ij}} - C/r_{ij}^{6} \end{equation}$

(14)

Because the exponential term converges to a constant when 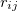$r_{ij}$ goes to 0, the Buckingham potentials might turn over when 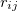$r_{ij}$ becomes small. This may be problematic in computer modeling (as ‘nuclear fusion’ can occur) ³⁴.

Fig. 2.6 shows these three empirical potentials. In general, all of them reproduce the strong repulsion at small distances and softer Coulomb attraction at large distances.

$\includegraphics[scale=1.0]{chapter2/pdf/Fig2.png}$

Figure 2.6: Three typical types of empirical models.

Pair potentials describe well for the inert gases and ionic systems. However, they fail in two cases. Firstly, they do not have environmental dependence. For the metallic system with defects, the individual atom near defect site must be very different from other atoms. This issue is considerd in semi-empirical models. Similary, pair potentials are generally inadequate for covalent systems, where many-body effects become important. Pair potentials do not account for the directional nature of the bond, and hence they always favor close-packing structures whereas most of the covalently bond crystals have open structures. Therefore, the three-body term and even higher body terms need to be introduced to describle the bond angle, torsion effects, and so on.

For the simulation of organic and bio-organic systems, people usually build the so called force field which encapsulates both bonded terms that are linked by covalent bonds, and nonbonded terms describing the long-range electrostatic and vdW forces. And force field contains the necessary building blocks for the calculation of energy and force (such as atom types, atomic charges, rules for atom-types, and so on). For details, one can refer to some popular force fields like AMBER ³⁵, CHARMM ³⁶ and GROMOS ³⁷.