2 Local optimization

Local optimization is to drive the initial configuration to the state of local energy minimum at an external pressure (temperature) condition. Energy evaluation at the given force field is the key factor at this step.

For a given 3D periodic system with 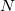$N$ atoms, the interactions are often expressed in terms of potential functions. The potential function

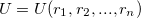$\begin{equation} \label{eq:total_ energy} U = U(r_{1}, r_{2}, ..., r_{n}) \end{equation}$

(8)

describes how the potential energy of a system of 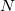$N$ atoms depends on the atomic coordinates $r_ i$ .

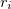One can employ the potential function for a particular system at different levels, namely, empirical potentials, semi-empirical potentials and quantum-mechanics-based potentials.