Image 1 Caption: For the Sun, the solar sidereal rotation rates for solar latitudes 0°, 15°, 30°, 45°, and 60° from r/R_☉=1/2 to the solar photosphere (i.e., r/R_☉=1).

Image 1 clearly shows the differential rotation of the solar interior.

Features:

1. The horizontal axis is radius in units of the solar radius defined to be at the point optical depth 2/3 into the solar photosphere (see Wikipedia: Solar radius).

   Note 1 R_☉ = 6.957*10**8 m = 0.004650 astronomical units (AUs) = 109.1 Earth equatorial radii. This value may be a mean value: the source Wikipedia: Solar radius is a bit unclear.

2. The vertical axis is frequency f=Ω/(2π) measured in nanohertz (1 nHz=10**(-9) Hz). Note a frequency of once per year ∼ 1/(π*10**7 s) ≅ 3*10**(-8) Hz = 30 nHz.

3. To convert the plotted frequencies to sidereal period (i.e., period relative to the observable universe) in days use the following formula:

         p = (11574.074074 ... days)/f_nHz ≅ ( 26.60706683695189 ... days)/(f_nHz/435 nHz) ,

   where f_nHz is frequency in nanohertz and 435 nHz is a fiducial value for the internal solar sidereal rotation rate as Image 1 itself shows.

   

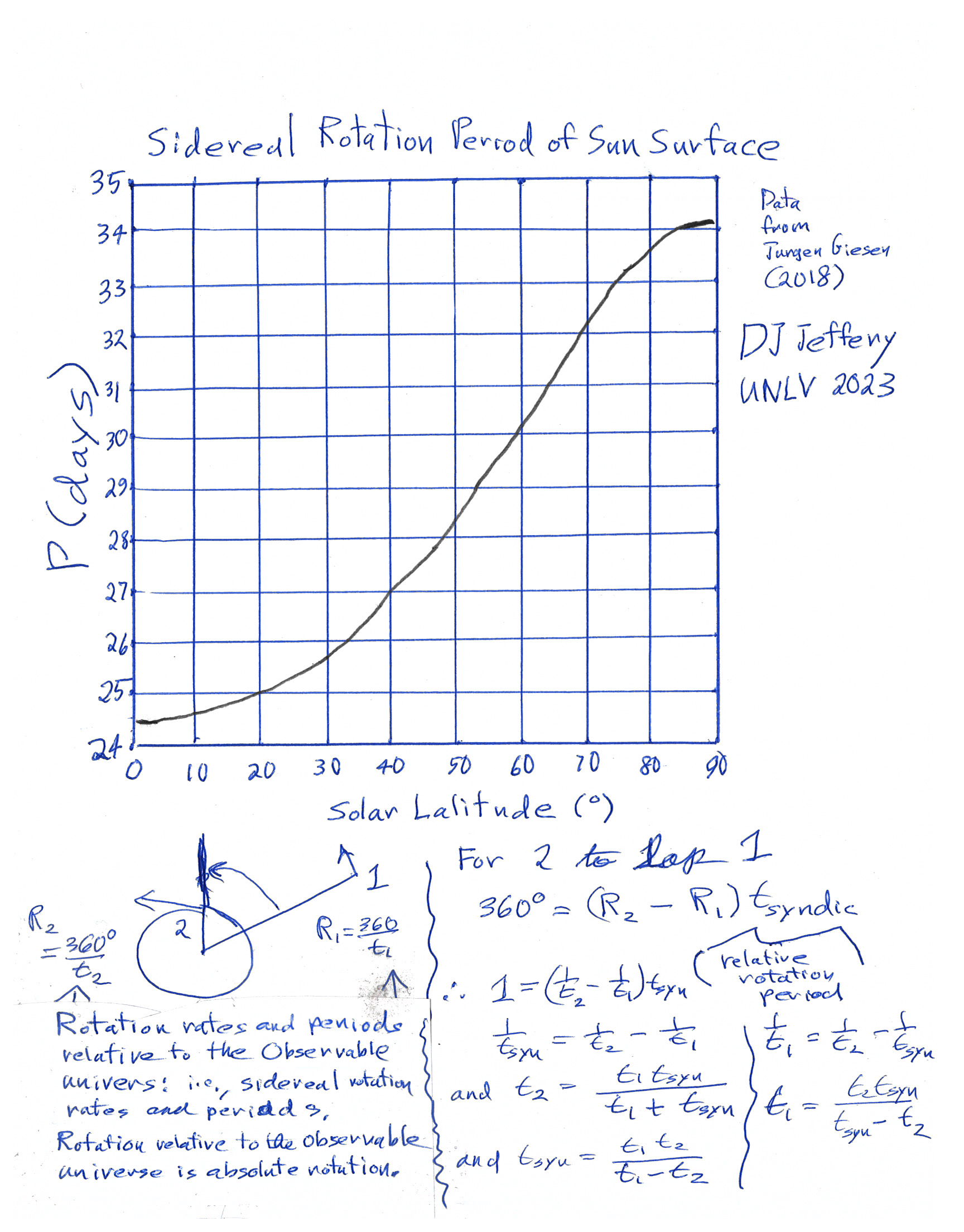
4. Image 2 Caption: This plot shows the solar sidereal rotation period (i.e., the rotation period relative to the observable universe) as a function of solar latitude.

5. The values for the solar sidereal rotation period obtained form formula values above and frequencies obtained casual inspection of Image 1 are probably NOT so good. The Image 1 gives 0° and 60° latitude surface solar sidereal rotation periods as, respectively, 25.7 days and 31.3 days, but but the measured values are 24.47 days and ∼ 30.2 days as can be verified approximately by inspection of Image 2 (see also Wikipedia: Solar rotation: Sidereal rotation).

   Maybe Image 1 is NOT meant to be extrapolated to the solar photosphere.

   The observed 90° latitude limit surface solar sidereal rotation period is ∼ 34 days (see Image 2).

6. Remarkably, the rotation rate inward of about 0.65 R_☉ is nearly CONSTANT---the curves for the different solar latitudes converge to a nearly CONSTANT value of about 435 nHz implying a ∼ 26.6 day sidereal period as seen from the formula above.

   This means the deep interior region rotates nearly as if it were a rigid-rotor solid sphere even though it is NOT: it's a sphere of gas.

   The radius 0.65 R_☉ also approximately divides the inner solar radiative zone from the outer solar convective zone. The transition between these two zones is the tachocline.

7. How do we know about the solar rotation rates?

   The surface ones were mostly directly observed long ago by tracking the motions of sunspots: the sunspots largely move with the solar rotation rates for solar latitudes where they appear.

   Galileo (1564--1642) and his contemporaries used sunspots to determine early solar rotation rates (see Wikipedia: Solar rotation: Using sunspots to measure rotation: Galileo's Letters on Sunspots (1613)).

   The interior solar rotation rates were learnt from helioseismology: the study of solar oscillations. The solar oscillations are observed on the surface and can then be used to infer the interior solar rotation rates and other interior features.

8. For more on solar rotation, see Solar rotation videos below (local link / general link: solar_rotation_videos.html):

   EOF

Images:

1. Credit/Permission: © Global Oscillation Network Group (GONG), 2008 (uploaded to Wikipedia by User:KeepOpera, 2010) / Creative Commons CC BY-SA 3.0.
   Image link: Wikipedia: File:Tachocline.gif.
   
2. Credit/Permission: © David Jeffery, 2023 / Own work.
   Image link: Itself.
   Data source: Jurgen Giesen, 2018. See Jurgen Giesen: Solar Rotation Applet and Jurgen Giesen: Sidereal Rotation Period of the Sun (days).