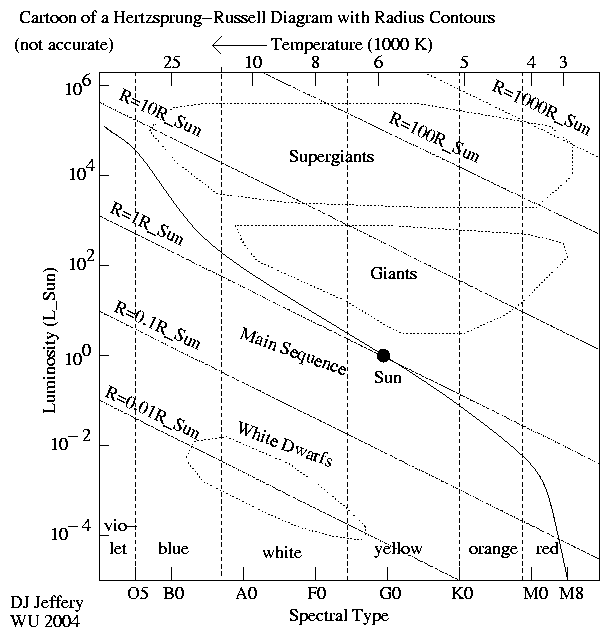
Caption: A cartoon of a Hertzsprung-Russell (HR) diagram with contour lines of constant radius (NOT quantitatively accurate) (FK-428).

Features:

1. The luminosity of a star approximated as a blackbody radiator is

   L = (4πR**2)*σT**4 ,

   where T is the effective temperature (a sort of average photospheric temperature), R is photosphere radius, the Stefan-Boltzmann constant σ = (5.670374 19 ...)*10**(-8) W/*m**2/K**4 (exact) (see NIST: Fundamental Physical Constants --- Complete Listing 2018 CODATA adjustment)), and Stefan-Boltzmann law of blackbody spectra F = σ*T**4 is used to get the emitted flux per unit area.

2. On a HR diagram (which is a log-log plot), the luminosity formula becomes the logarithmic formula

   log(L) = 4*log(T) + 2*log(R) + log(4πσ) .

   Recall that photospheric temperature (roughly the same as the effective temperature) increases to the left on a HR diagram in astronomy wrong-way fashion, and so log(L) increases/decreases going left/right.

3. The logarithmic luminosity log(L) plotted on an HR diagram gives contour lines of constant radius that are straight lines rising to the left with slope 4 which are separated by factors of 100 for every increase of 10 in radius (as follows clearly from the formula L = (4πR**2)*σT**4). This behavior is illustrated in the image.

4. Note for the contour lines of constant radius we have the following approximately:
   1. R = 0.01 R_☉ ≅ Earth equatorial radius R_eq_⊕ = 6378.1370 km crosses the white dwarf luminosity class. Therefore, typically white dwarfs are about the size of the Earth.
   2. R = 0.1 R_☉ just intersects the main sequence for M dwarfs.
   3. R = 1 R_☉ just intersects the main sequence for solar mass stars, but because the intersection angle is small stars near the Sun on the main sequence will have R ≅ 0.1 R_☉.
   4. R = 10 R_☉ crosses the supergiant and giant luminosity classes.
   5. R = 100 R_☉ crosses the supergiant luminosity class.
   6. R = 1000 R_☉ crosses the supergiant luminosity class just barely.
   7. For other R values, you must mentally interpolate, the contour lines of constant radius.

   We must emphasize that the HR diagram in the image is just a cartoon, and therefore it and the luminosity classes shown are very approximate.

5. Other behaviors are:
   1. For a fixed effective temperature T, the luminosity L increases with the size of the radiator: i.e., with radius R. Thus, R↑ L↑.

   2. For a fixed luminosity L, radius R increases as temperature T decreases. To explicate, as temperature decreases, the flux (which is energy per unit time per unit area) of a blackbody radiator decreases. Area and therefore radius must rise to compensate if luminosity is held fixed. Thus, T↓ R↑.

6. We can the inverse of the above formula L = (4πR**2)*σT**4 to determine to good approximation the stellar radius: i.e., the radius of the photosphere (FK-429). The inverse formula is

   R = sqrt[L/(4π*σT**4)] .

   Note that we CANNOT measure stellar radius directly in almost cases because almost always stars CANNOT be resolved. The finite size of observed stars is a combination of twinkling (AKA scintillation) and diffraction. The former mostly for the naked eye and the latter mostly for the telescope where twinkling is reduced by aperture averaging.