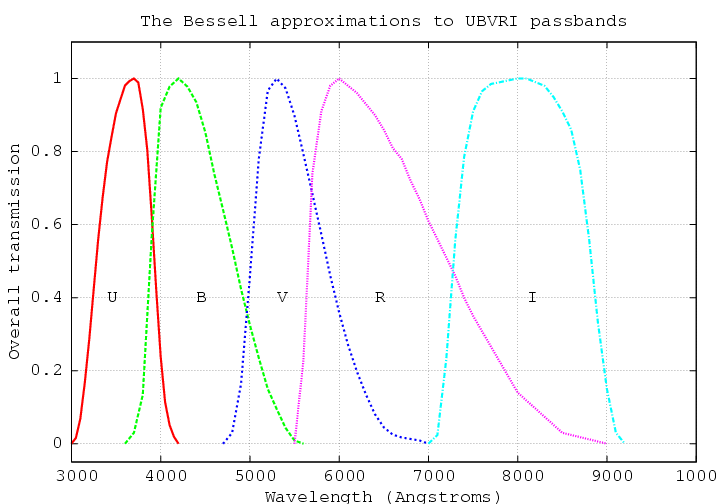
Caption: The passbands (AKA transmission functions) normalized to 1 for UBVRI filters of photometry.

The UBVRI filters are most traditional set of passbands, but there are many other sets. It seems every time someone builds a new advanced telescope, they have to invent a new set of passbands for it. There are transformation relationships between the sets of passbands.

Features:

1. A passband is convolved with incoming radiant flux (AKA flux) to produce a passband magnitude.

   Convolution in this context means you integrate the flux over wavelength weighted by the passband.

   Passbands give you a measure of the flux in a wavelength band.

   This kind of observation is photometry. It's cruder than spectroscopy in wavelength discrimination of integrated flux, but much more sensitive. Less observing time (integration time) is needed and you can go much fainter.

   Spectroscopy is, in fact, very narrow passband photometry.

   Photometry and spectroscopy are complementary and/or supplementary to each other depending on the case.

2. Why are passbands NOT simply rectangular functions?

   Passbands of that sort are hard to implement technologically especially in the past. So traditional passbands are just smooth functions that go to zero rapidly enough as one goes to ±∞ that they can be integrated over wavelength to give a finite value.

3. Yours truly suspects the displayed passbands neglect the effects of the Earth's atmosphere.

4. Below is a table specifying the UBVRI passband system.

   _________________________________________________________________
   
   Table:  UBVRI Passband System
   _________________________________________________________________
   
      Band        λ          Δλ            Comment
            (microns = μm)  (μm)
   _________________________________________________________________
   
        U       0.365       0.066          U stands for ultraviolet.
        B       0.445       0.094          B stands for blue.
        V       0.551       0.088          V stands for visual.
        R       0.658       0.138          R stands for red.
        I       0.806       0.149          I stands for infrared.
   _________________________________________________________________ 

   Notes:
   1. Reference: The data are from Wikipedia: Photometric system: Filters.
   2. The wavelength λ is the mean band wavelength defined in some sense.
   3. The Δλ is the full width half maximum of the transmission function of the passband.
   4. Instead of V for visual, the V should have been called Y for yellow color band (∼ 0.570--0.590 μm) since V light looks yellow. But it's too late now.
   5. For the individual passbands, see the linked symbols U, B, V, R, I.

5. The symbol for apparent magnitude in U, etc. is just U etc. itself.

6. The symbol for absolute magnitude in U etc. is usually M_U etc.

7. The apparent brightness of stars is usually specified by specifying their apparent magnitude in V.

   Recall that in astronomy, "apparent" means as seen from the Earth, and NOT seeming or false.

8. Probably V is used to specify apparent brightness of stars because the human eye rates star brightness in much the same order as rated by V. Or maybe it's just tradition.